Последовательная и параллельная реализация метода верхней релаксации при решении задач математической физики

⇓Загрузить PDF (рус.)

Электронное моделирование. —2000. —№ 6.−c.3−12.

ПОСЛЕДОВАТЕЛЬНАЯ И ПАРАЛЛЕЛЬНАЯ РЕАЛИЗАЦИЯ МЕТОДА ВЕРХНЕЙ РЕЛАКСАЦИИ ПРИ РЕШЕНИИ ЗАДАЧ МАТЕМАТИЧЕСКОЙ ФИЗИКИ

Каневский Ю.С., Лепеха В.Л., Сергиенко А.М. (Национальный технический университет Украины “КПИ”, Киев,
Выжиковски Р. (Ченстоховский политехнический ин-т, Польша)

АнотацияРассмотрена реализация метода верхней релаксации при решении задач математической физики методом конечных элементов. Проанализированы возможные варианты записи матриц в разреженном формате. Показаны последовательная и параллельная формы реализации данного метода. Приведены экспериментальные результаты решения задач математической физики с помощью данного метода.

АнотаціяРозглянуто реалізацію методу верхньої релаксації при розв’язуванні задач математичної фізики методом кінцевих елементів. Проаналізовано можливі
варіанти запису матриць в розрідженому форматі. Показано послідовну та паралельну форми реалізації даного методу. Наведено експериментальні результати розв’язування задач математичної фізики з використанням даного методу.

Ключевые слова: метод конечных элементов, разреженная матрица, метод верхней релаксации.

Введение. Решение крупных научно-технических проблем стало возможным благодаря применению математического моделирования и новых численных методов. Быстрое развитие микроэлектроники и создание высокопроизводительных ЭВМ привели к появлению нового способа теоретического исследования сложных процессов, допускающих математическое описание, – вычислительного эксперимента [1].

При решении задач математической физики (моделировании тепловых, электромагнитных, механических и др. процессов) достаточно часто используется метод конечных элементов (МКЭ). При всем своем разнообразии задача, в конечном итоге, сводится к решению (зачастую многократному) систем линейных алгебраических уравнений (СЛАУ) (Ax = y), где A – является сильно разреженной матрицей.

С целью экономии памяти и ускорения вычислительного процесса целесообразно оперировать матрицами, записанными в разреженных форматах. При записи матрицы в разреженном формате для решения системы линейных алгебраических уравнений (СЛАУ) целесообразно использовать итерационные методы, поскольку применение прямых методов влечет за собой изменение структуры матрицы, и, как правило, приводит матрицу к ленточному или плотно заполненному виду [2].

Задачи математической физики предполагают большой объем вычислений. При этом сложность современных задач, выраженная в числе математических операций, и требования к точности полученных результатов (что при использовании итерационных методов решения СЛАУ также увеличивает необходимый объем вычислений) растут быстрее, чем производительность вычислительных средств. Поэтому, учитывая все возрастающий объем вычислений и фундаментальные ограничения на скорость переключения элементов и распространения сигналов, достаточно актуальной проблемой становиться задача распараллеливания вычислений.

Данная статья посвящена последовательной и параллельной реализации метода верхней релаксации.

Краткое описание метода. Метод верхней релаксации относится к треугольным методам [1]. В нем оператору B соответствует нижняя треугольная матрица B = D + ω•L, где D – диагональная матрица; L – нижняя треугольная матрица из разложения исходной матрицы A = L+D+U; ω – коэффициент релаксации (в случае верхней релаксации 1 < ω < 2).

Рассматриваемый метод хорошо известен, поэтому при его описании
ограничимся результирующей вычислительной формулой [1]:

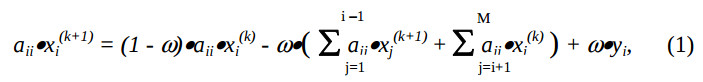
где ω – коэффициент релаксации; k – номер итерации; M – размер матрицы; i,j – 1, 2, …, M; найденное x_i^(k+1) сохраняется с замещением x_i^(k).

Поскольку на матрицу не накладывается требование симметричности, ее целесообразно нормализовать. Тогда результирующая формула примет следующий вид:

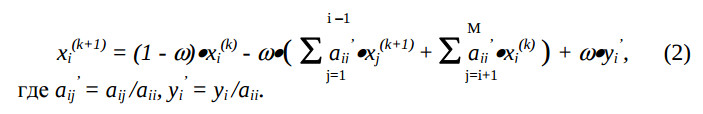
Метод верхней релаксации отличается простотой реализации и экономичностью. К его недостаткам следует отнести определенную сложность при выборе оптимального коэффициента релаксации.

Выбор формата представления матрицы. Под разреженным форматом представления подразумевают такую запись матрицы, при которой в памяти ЭВМ хранятся только значения ненулевых элементов и их место расположения в матрице. В настоящее время описано достаточно много таких форматов [3]. Однако специфика реальных задач или матриц может потребовать конкретного представления матрицы. Опишем подробно представление матрицы в разреженном строчном формате RR(C(O)), который можно достаточно эффективно применять в методе конечных элементов.

В данном формате значения ненулевых элементов и соответствующие им столбцовые индексы хранятся по строкам в двух массивах, например, для матрицы X соответственно в массивах XN и JX. Кроме того, в RR(C(O)) используется массив указателей (IX), i-й элемент которого указывает позицию в предыдущих двух массивах, с которой начинается описание i-й строки матрицы X. В этом формате произвольная матрица

будет представлена в виде трех массивов:

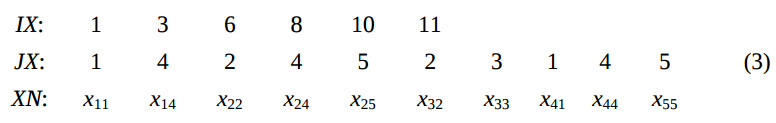
Описание реализующей программы. При решении СЛАУ матрица предварительно нормализуется и представляется в виде (3). Правая часть, разделенная на диагональ, записана в векторе y. Искомое решение записывается в векторе x. Вычисления будем производить по формуле (2), которая будет представлена в виде

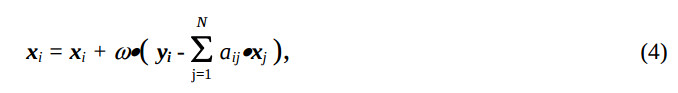
причем вновь вычисленное значение x_i будет записываться на место старого.

Рассмотрим фрагмент (основной цикл) программы, написанной на языке Си. В нем e2 – заданная погрешность вычислений, n – число строк матрицы A; w – коэффициент релаксации; e, i, j, s – промежуточные параметры.

while(e > e2)
{         /∗ вычисление X(k+1) ∗/
     for (i = 1; i < n; i++)
     {    /∗ вычисление Xi(k+1) ∗/
         s = Y[i] - X[i];
         for (j = IA[i]; j < IA[i+1]; j++)
            s = s - AE[AN[j]] ∗ X[JA[j]];
         X[i] = X[i]+w ∗ s;
      }
          /∗ вычисление e - проверка на сходимость ∗/
      void shod(); shod();
}

где shod() - процедура проверки на сходимость, например, е = MAX(Ax-y).

Элементы вектора X вычисляют, начиная с первого. Первоначально параметру s присваивают значение Y[i] - X[i], поскольку элемент a_ii = 1. Затем вычисляют значение, записанное в скобках формулы (4). Для этого параметру j присваивают адрес первого элемента i-й строки. Все элементы строки расположены последовательно, начиная с IA[i] и заканчивая IA[i+1]-1. На j позиции векторов JA и AN находятся адреса соответственно элементов векторов X и AE, которые должны быть перемножены между собой и накоплены в s. По окончании цикла накопления вычисленное значение умножается на коэффициент релаксации w и суммируется со значением X[i]. По окончании вычисления вектора X^(k+1) проводится оценка сходимости в соответствии с выбранным критерием. Объем вычислений, необходимый для такой оценки, может оказаться не ниже вычислительной сложности формирования вектора X, поэтому в некоторых случаях проводить оценку целесообразно через определенное число итераций.

Рассмотрим двумерную задачу упругости с двумя степенями свободы (изгиб балки под воздействием сосредоточенной нагрузки (рис.1)).

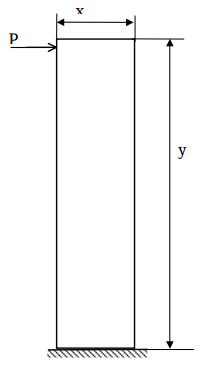
Проанализируем два варианта: с предварительным оценочным расчетом X⁰ = F(x, y, P) и при X⁰ = 0. Полученные расчетные данные сведены в табл. 1 (здесь x,y - параметры, определяющие сетку; в ячейках указано число итераций, необходимых для решения задачи при ε = MAX(Ax - y) = 0,0001).

Таблица 1

x	30	50	80	40	80
y	100	100	100	200	200
X0 = F(x,y,P)	111	108	112	203	185
X0 = 0	581	852	438	2201	1202

Как видно из табл. 1 метод верхней релаксации сходится очень быстро при наличии приближенного решения. В противном случае, число итераций может быть достаточно большим.

Распараллеливание вычислений. Решетчатый граф данного алгоритма размещается в параллелепипеде размерности N × M × K.

Граф алгоритма выполнения k-й итерации не намного отличается от графа умножения матрицы на вектор.

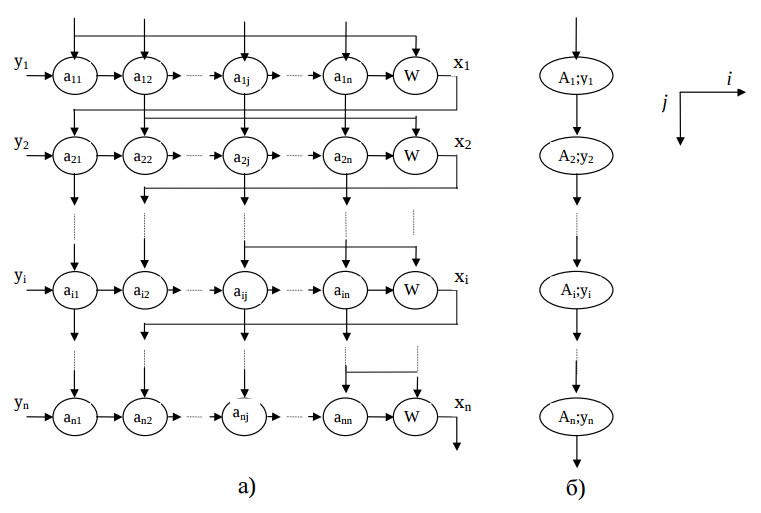
Как видно из рис. 2,a, граф является регулярным. Базовая операция, соответствующая каждому узлу графа, имеет вид: S = S + a • b. Учитывая разреженность матрицы, спроецируем граф по оси i, с тем чтобы в каждом узле находилась строка матрицы А и соответствующий ей элемент вектора y (рис 2,б). Такая схема решения задачи имеет существенный недостаток. Как известно, в методе верхней релаксации при вычислении элемента x_i используются уже вычисленные в этой итерации элементы x_j (j<i). В связи с этим, при переходе к вычислению следующего элемента необходимо вводить задержку (на N-1 тактов) для ожидания вновь вычисленного элемента.

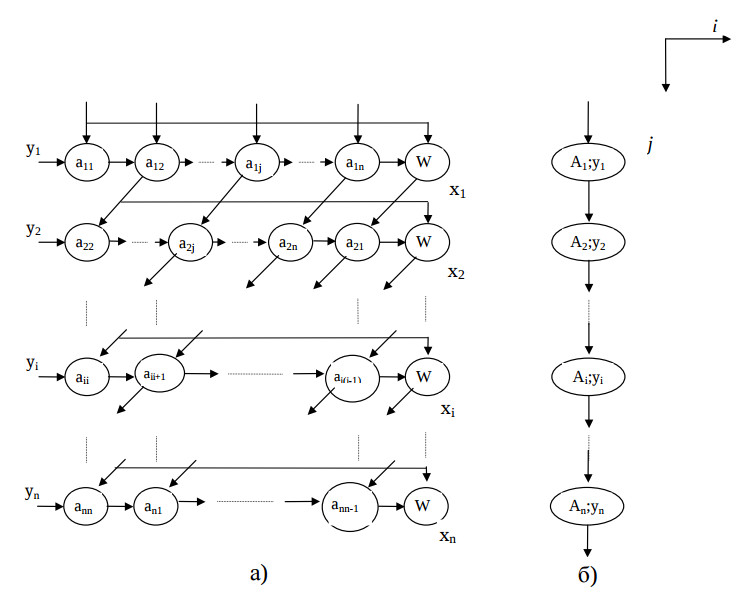
Частично трансформируем исходный граф (рис. 3,а). Спроецируем его вновь на ось i (рис. 3,б.). В данной ситуации задержка в каждом узле составит 1 такт. Такая схема вычислений будет достаточно эффективной при плотно заполненной матрице.

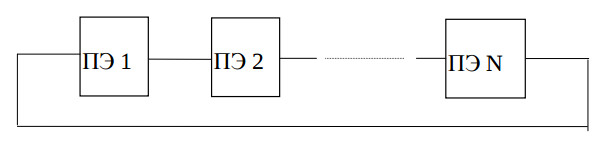
В случае применения линейной вычислительной структуры (рис. 4), соответствующей графу, приведенному на рис. 3,б, загруженность процессорных элементов (ПЭ) составит - N/(N+1). Однако для разреженной матрицы, загруженность i-го ПЭ будет равна - r_i/(N+1), где r_i - число ненулевых элементов в i-й строке. Учитывая, что r_i << N, можно сделать вывод о том, что выполнение данной задачи на структуре с N ПЭ крайне не эффективно.

Значительно больший интерес может вызвать ограниченный параллелизм (решение задачи на K (K << N) ПЭ). Для этого склеим соседние вершины графа таким образом, чтобы в графе, приведенном на рис. 3,б осталось K вершин. Структурная схема такого вычислителя аналогична рассмотренной (см. рис. 4), с той лишь разницей, что число ПЭ равно K. В памяти процессорного элемента находятся s (s = N/K) строк матрицы A, s элементов вектора y, а также те элементы вектора x, которые участвуют в вычислениях, проводимых в данном ПЭ. По мере вычисления значений вектора x, они передаются в другие ПЭ. В данном случае загруженность ПЭ будет не меньше Σr_i /(Σr_i + N). При этом желательно склеивать вершины графа таким образом, чтобы число передач между ПЭ было минимальным. Процессорные элементы должны работать в синхронном режиме (каждый ПЭ начинает (k+1)-ю итерацию только после получения всех значений, вычисленных в других ПЭ во время k-й итерации).

В табл. 2 показано расписание работы вычислительной структуры, состоящей из трех ПЭ, при решении СЛАУ с матрицей, изображенной на рис. 5.

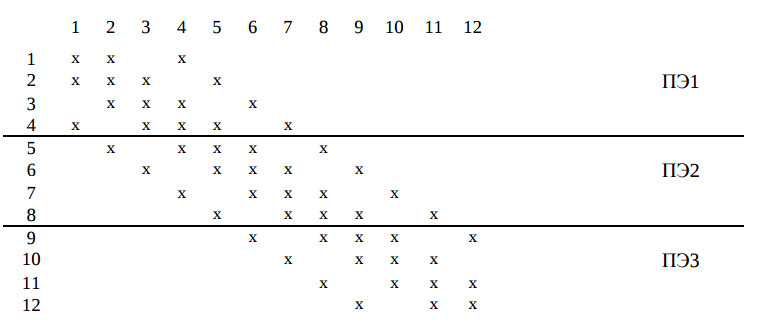
Таблица 2.

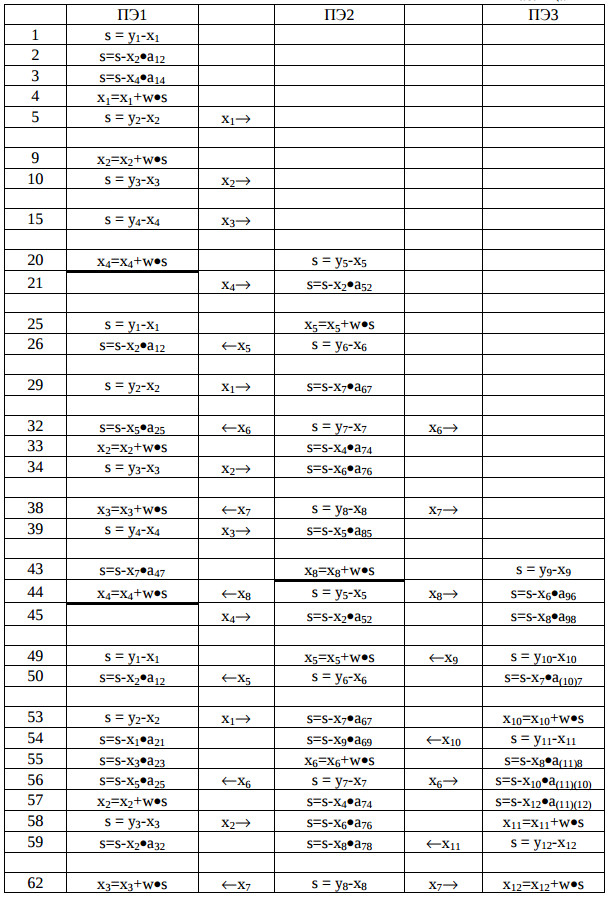
В 1-й колонке показан номер такта работы структуры, во 2-, 4-, 6-й – операция выполняемая в ПЭ, в 3-, 5-й – передаваемое значение; стрелочкой указано направление передачи. Предполагается, что вновь вычисленное значение x_i передается в ПЭ, где оно будет использовано сразу же после и на фоне вычислений. Такую возможность обеспечивают, например, процессорные матрицы на базе сигнальных процессоров типа TMS320C40, DSP9600, ADSP21000 и др. Как видно, в случае линейной структуры с локальными связями и при возможности обмена информацией на фоне вычислений можно добиться практически 100% загруженности оборудования.

Если обмен информацией на фоне вычислений невозможен или при построении параллельной вычислительной системы с общей шиной то загруженность ПЭ можно определить как К_в/(К_в+К_п), где К_в - число вычислений в ПЭ, К_п - число необходимых передач после каждой итерации.

Оценим загруженность ПЭ на примере решения описанной задачи упругости при x = 80, y = 200 (с учетом двух степеней свободы - решающее поле - 160×200). При распараллеливании вычислений и загрузке ПЭ, как это видно из рис. 4, каждый ПЭ (кроме крайних) по окончании итерации должен передать соседним 320 вновь вычисленных значений и принять также 320 значений, вычисленных в соседних ПЭ. Таким образом, принимают 160 значений. Рассмотрим загруженность линейной структуры с локальными связями и загруженность структуры с общей шиной. При этом будем предполагать, что время, необходимое для выполнения операции пересылки, равно времени выполнения арифметической операции. Загруженность арифметико-логоческого устройства (АЛУ) процессорных элементов условно не учитывается.

Рассмотрим распараллеливание задачи на четырех ПЭ. В каждом ПЭ вычисляются 8000 значений вектора x, при этом для вычисления каждого элемента вектора необходимо выполнить 15 арифметических операций. Тогда число арифметических операций, выполняемое в каждом ПЭ для одной итерации, К_в = 120000. При этом число операций пересылки для линейной структуры - К_п = 640, а для структуры с общей шиной - К_п = 960. Загруженность в данном случае практически стопроцентная. Аналогично можно получить К_в и К_п для другого числа ПЭ.

В табл. 3, приведены соответствующие данные при отображении данной задачи на различное число ПЭ.

Таблица 3

Число ПЭ	Вычислительная структура
	Линейная			С общей шиной
	Кв	Кп	загру- женность ПЭ	Кв	Кп	загру- женность ПЭ
4	120000	640	≈ 100%	120000	960	≈ 99%
8	60000	640	≈ 99%	60000	2240	≈ 96%
16	30000	640	≈ 98%	30000	4800	≈ 86%
32	15000	640	≈ 96%	15000	9920	≈ 60%

Как видно из таблицы 3, загруженность вычислительной структуры с локальными связями достаточно высока даже при большом числе ПЭ. Загруженность же структуры с ОШ резко снижается при увеличении числа ПЭ, а с учетом времени для организации обмена сообщениями (на практике время, необходимое для пересылки одного значения, равно времени выполнения 10 - 1000 арифметических действий) она может упасть настолько, что возникает вопрос о целесообразности самого распараллеливания.

При существенном влиянии пересылок на снижение загруженности ПЭ интерес вызывает асинхронный режим вычислений. В таком режиме межпроцессорный обмен информацией выполняется после выполнения несколько итераций (склеивание итераций). Такой режим работы при построении вычислительной структуры с локальными связями и фоновым обменом информацией исключил бы необходимость синхронизации двух процессов (вычисления и передачи информации), что упростило бы программирование задачи. При построении структуры с ОШ уменьшение операций пересылки привело бы к повышению загруженности вычислительной структуры. Метод верхней релаксации предполагает возможность блочной реализации, и, поэтому, при таком склеивании задача будет сходиться [2]. В табл. 4 приведено число итераций, необходимых для решения описанной задачи при различном числе ПЭ и склеенных итераций.

Табица 4

ПЭ	Число склеенных итераций
	1	2	3	4
8	185	508	672	856
16	185	678	891	1644
32	185	880	1026	1740

Как видно из табл. 4, при использовании метода верхней релаксации строить асинхронно работающую параллельную вычислительную систему нецелесообразно, поскольку резко возрастает число необходимых для решения СЛАУ итераций, и, как следствие – число обменов информацией.

Заключение. Для решения задач математической физики с записью матриц в разреженном строчном формате для решения СЛАУ можно применять метод верхней релаксации. Метод достаточно прост в реализации на последовательных вычислительных средствах и не требует избыточной информации. Он особенно эффективен при наличии приближенного решения, например, при решении нелинейных задач, предполагающих последовательное решение большого числа СЛАУ. При этом решение каждой системы является приблизительным решением последующей. Метод хорошо распараллеливается. В случае применения линейной вычислительной структуры с локальными связями достигается практически 100%-я загруженность. При использовании структуры с общей шиной ее загруженность зависит от объема и скорости передачи информации и может быть низкой.

Литература

1. Самарский А.А., Николаев Е.С., Методы решения сеточных уравнений. -М.: Наука, 1978. - 592 с.

2. Воеводин В.В., Кузнецов Ю.А., Матрицы и вычисления. – М.: Наука,1984. - 320 с.

3. Писанецки С. Технология разреженных матриц. - М.: Мир, 1988. – 411 с.

⇓Загрузить PDF (рус.)