Досконалий кістяк графа алгоритма
А.М.СЕРГІЄНКО, к.т.н., с.н.с.
ДОСКОНАЛИЙ КІСТЯК ГРАФА АЛГОРИТМА
Дано визначення досконалого кістяка алгоритма, показано, що за його допомогою складається розклад за стратегією найскорішого призначення і запропоновано алгоритм його побудови. Досконалий кістяк алгоритма дає змогу на його основі ефективно представити алгоритми в САПР обчислювальних спеціалізованих засобів і покращити процес їхньої структурної оптимізації.
The perfect maximum spanning tree (PMST) of the algorithm is proposed. It was shown that the ASAP – time table is built on the base of PMST in the natural way. The algorithm of PMST deriving from the SDF graph is proposed. PMST gives the opportunity to represent the algorithm effectively and to optimize the structural solution more quickly in the system-level CAD tools.
Статичне складання розкладу алгоритму – це основна операція при синтезі як паралельних програм, так і паралельних обчислювачів. Найбільш поширений метод складання статичного розкладу оснований на інтерпретації графа синхронних потоків даних (ГСПД) [1].
В роботі [2] запропоновано представляти ГСПД в багатовимірному просторі у вигляді конфигурації алгоритма (КА) KG=(K,D,A), де K – матриця векторів-вершин Ki, що відповідають операторам алгоритма, D – матриця векторів-дуг безпосередніх інформаційних залежностей між операторами, A – матриця інцидентності ГСПД. В простому випадку можна використати трьохвимірний простір. Тоді в векторі-вершині Ki = <ki,si,ti> координати ki,si,ti дорівнюють типу оператора (наприклад, k=1 – множення), номеру процесорного елемента (ПЕ), де виконується цей оператор і такту, в якому записується в регістр або пам”ять результат цього оператора.
Еквівалентним структурним рішенням обчислювача відповідають КА, які відрізняються різними матрицями К і D. Однією з умов коректності КА є та, що серед векторів Ki не повинно бути двох однакових. Так як між матрицями КА є лінійний зв”язок, то матрицю D можна обчислити з виразу
D = КА. (1)
КА розщеплюється на просторову конфігурацію і конфігурацію подій, яким відповідають структура обчислювача і розклад виконання операторів. При цьому вектори Ki = <ki,si,ti> розкладаються на вектори KSi=<ki,si>, що відповідають координатам ПЕ, і вектори KТі = <ti>, які означають моменти виконання відповідного операторів в ПЕ KSi. Тоді часова складова DТi = <ti>вектора залежності Di дорівнює затримці ti пересилки або обробки відповідної змінної. Конфігурація подій представляє собою розклад виконання алгоритму, а його пошук – це знаходження значень KТі.
Якщо в ГСПД є цикли міжітераційних залежностей, то сума векторів-дуг Dj, що входять в будь-який з контурів графа дорівнює нулю, тобто для i-го контура
∑ bi,j Dj = 0,
де bi,j – елемент i-го рядка цикломатичної матриці ГСПД. В такому контурі можна виділити вектор-дугу DВj = <0,0,–kL> міжітераційної залежності, який означає затримку на k ітерацій, де L – тривалість цикла обчислень або ітерації алгоритма в тактах.
В роботі [2] запропоновано знаходити координати векторів Ki на основі кістяка ГСПД. Кістяк – це мінімальний зв`язний підграф графа. Число дуг m в кістяку дорівнює числу вершин n без однієї, тобто m = n − 1. Кістяк одержують послідовним видаленням будь-яких дуг, які називають поперечними, доки граф зберігає зв`язність [3]. В нашому випадку, будемо видаляти тільки ті поперечні дуги, які кінцем інцидентні вершинам, в які входять кілька дуг.
Конфігурація алгоритма, який заданий кістяком, має таку властивість, що
Dо = KAо; (2)
K = Dо Aо-1; (3)
де Aо – матриця інцидентності кістяка ГСПД. Відмітимо, що матриця векторів-дуг Dо має розміри rm = rn, де r − розмірність простору, причому до кістяка добавлена базисна дуга, яка власне не належить до кістяка, а зв`язує початок системи координат з деякою вершиною кістяка.
Для cпрощення, нехай кожен оператор алгоритму виконується рівно за один такт. Тоді пошук розкладу алгоритму, граф якого є кістяком, полягає в наступному. Необхідно призначити всім векторам-дугам координати DТi = 1 і знайти KT з відношення (3). Решту координат векторів Ki знаходять з умов коректності КА. Це вийде найбільш швидкий розклад, так як кожен оператор виконується за один такт і немає зайвих затримок. Якщо одержана матриця К не задовольняє критерій оптимальності, наприклад, якихось ресурсів необхідно занадто багато, то деякі вектори DТi, зв`язані з цими ресурсами, змінюють і повторюють пошук розкладу.
Якщо мається на увазі алгоритм з графом загального виду, то має сенс шукати розклад на основі його кістяка, як показано вище з застосуванням відношень (1) і (3). Але при цьому з`являються складнощі з появою неправильних розкладів, які потрібно знаходити і вилучати під час комбінаторної оптимізації розкладу. Пошук розкладу в такий спосіб суттєво залежить від вибору кістяка ГСПД. Щоб вибрати кістяк, який би завдавав менше клопоту при пошуку розкладу, розглянемо фактори, які викликають появу некоректного розкладу.
По-перше, в графі може бути стягуюча дуга, тобто така, що замикає маршрут з кількох інших дуг, як наприклад: D4 = D1 + D2 + D3. При цьому виникає неприпустима ситуація, коли стягуюча дуга входить в кістяк, тому що часові складові векторів-дуг, які з`єднає ця дуга, можуть бути від`ємними. Приклад такого випадку показаний на рис.1,а.
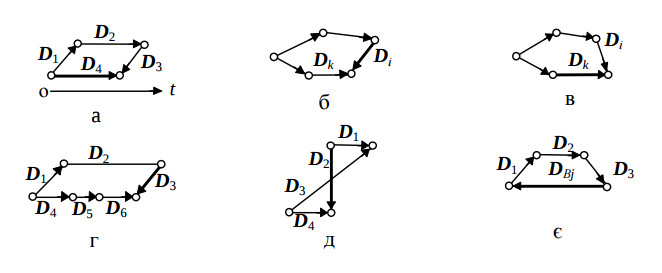
Якщо прийняти вісь оt за вісь часу, то часова складова вектору D3 виявиться від`ємною.
По-друге, в графі є поперечні дуги, тобто такі дуги, які не є стягуючими, але додавання яких до кістяка робить в графі контури [3]. При цьому поперечна дуга Di може виявитися такою, що якщо після визначення розкладу по (3) знайти координати Di з виразу (1), то може скластись ситуація, коли DTi< 0, тобто такий розклад буде неправильним. Така поперечна дуга Di показана на рис.1,б. Поперечні дуги не входять в кістяк за визначенням. І в більшості випадків якщо вдало вибрати поперечну дугу, наприклад, на рис.1.в, – не Di, а Dk, то можна побудувати відповідний кістяк, з допомогою якого одержати коректний розклад, використовуючи рівняння (3). Таким чином, якщо поперечна дуга входить в коротший маршрут з однієї вершини в другу, то завжди можна скласти коректний розклад.
Розглянемо такі поперечні дуги, наявність яких може призвести до неправильного розкладу. Таку дугу назвемо критичною поперечною дугою. В графі можуть бути рівнозначні маршрути з однієї вершини в іншу, наприклад, як на рис. 1,г, де D1 + D2 + D3 = D4 + D5 + D6. Тут критичною поперечною дугою є така, що замикає рівнозначний маршрут в контур, тобто D3. Також критичною поперечною дугою є така дуга, яка належить контуру, котрий формує підграф з декількома джерелами. Типовий такий підграф зображено на рис. 1,г і для нього D1 − D3 = D2 − D4 .
В обох випадках розглянуті підграфи належать до класу узгоджених графів. Узгодженим графом називається граф, в кожному циклі якого кількість дуг – парна, а сума цих векторів-дуг дорівнює нулю [4]. Слід відмітити, що в кістяк необхідно включити повністю хоча б один з рівнозначних маршрутів. Тому якщо в початковому графі відмітити всі критичні поперечні дуги, то частина їх обов`язково попаде в результуючий кістяк, що може привести до неправильного розкладу. Тоді щоб одержати коректний розклад, необхідно в кістякові відмітити вершини, в які заходять критичні поперечні дуги і при пошуку розкладу перевіряти і коректувати часові складові дуг, які заходять у відмічені вершини.
По-третє, якщо алгоритм циклічний з міжітераційними залежностями, то вони в ГСПД відповідають дугам міжітераційних залежностей DВj , причому, наприклад, для графа на рис.1,є DВj = − (D1 + D2 + D3) і DВTi = −L.
Вищеперелічені фактори необхідно враховувати при складанні розкладу. Щоб таких врахувань була мінімальна кількість, пропонується використовувати такий кістяк ГСПД, який спеціально підібраний для знаходження розкладу. Назвемо такий кістяк досконалим. Враховуючи викладене вище, можна cформулювати наступне визначення.
Досконалий кістяк – це кістяк ГСПД, в якому: а) відсутні стягуючі дуги, б) відсутні дуги міжітераційних залежностей, в) дуги входять в найдовші маршрути, г) відмічені вершини, в які заходять критичні поперечні дуги.
Для досконалого кістяка можна довести наступні твердження.
Твердження 1. До досконалого кістяка належить критичний шлях алгоритму.
Доведення від супротивного. Нехай в досконалий кістяк не входить критичний шлях. Тоді в нього не входить деякий ланцюг дуг, що належать критичному шляху. Це означає, що через крайні вершини цього ланцюга проходить по кістяку або стягуюча дуга, або більш короткий маршрут, що порушує визначення досконалого кістяка.
Твердження 2. Розклад, побудований на основі досконалого кістяка і рівняння (3) відноситься до розкладу за принципом найскорішого призначення (ASAP).
Доведення. Жадібний алгоритм ASAP оснований на топологічному сортуванні (нумерації) вершин ациклічного графа алгоритма згідно з їхнім частковим порядком, починаючи з початкової вершини і в призначенні на ресурси вершин в порядку їхньої нумерації [5]. В досконалому кістяку, як і будь-якому графі, топологічне сортування, тобто розмітка вершин натуральними зростаючими числами, починається з вершини-джерела, продовжується на суміжних вершинах і закінчується на вершинах-стоках. Таким чином, відсортовані вершини формують яруси, причому номери вершин наступного яруса завжди більші номерів вершин попереднього
яруса, вершини якого виконуються раніше вершин наступного яруса [3].
Нехай вектор-вершини Ki=<k, si, ti> і Kj =<k, sj, tj> мають топологічні номери i i j , i < j і призначаються на ресурс k −го типу. Тоді, якщо одержано розклад типу ASAP, то момент виконання Ki повинен бути не більшим момента виконання Kj, тобто ti ≤ tj, якщо вершини призначаються на різні ресурси, ti < tj, якщо вони призначені на один і той самий ресурс, а якщо ці вершини зв`язані дугою, то різниця цих моментів буде мінімальною.
Дійсно, згідно з вимогою коректності КА, <k, si, ti> ≠ <k, sj, tj> і тоді в першому випадку, si ≠ sj, а ti не може бути більшим tj, в другому випадку si = sj, тоді повинно бути ti < tj. І в останньому випадку, оскільки вершини зв`язані дугою Di, часовій компоненті якої надано мінімальне значення, наприклад, 1 такт, то з рівності і Kj = Ki + Di виходить, що tj = tі+1.
На основі визначення досконалого кістяка і доведених тверджень можна запропонувати наступний алгоритм побудови досконалого кістяка. Слід відмітити, що в більшості випадків пошуку розкладу розглядають граф з однією вершиною-джерелом і однією вершиною-витоком. В даному випадку ГСПД без дуг міжітераційних залежностей має декілька джерел і декілька витоків, і відповідно, в ньому є кілька критичних шляхів.
Початкові дані: орієнтований ГСПД GA з mI джерелами і mO стоками. Результат – граф досконалого кістяка GO.
1. Видалити всі дуги міжітераційної залежності. Відмітити вершини, в які заходять критичні поперечні дуги. Вибрати поточне джерело (вершину вводу або кінцеву вершину дуги міжітераційнї залежності), для якого заданий (якщо заданий) мінімальний момент виконання, або джерело з номером 1. Задати пустий граф кістяка GO = Ø.
2. Знайти з поточного джерела до m0 стоків, які відмітити як поточні. Знайти критичні шляхи з поточного джерела в поточні стоки. Граф GO зробити рівним об`єднанню графа GO і цих критичних шляхів, тобто GO:=GO ∪ GCRk , де GCRk – критичний шлях з поточного джерела в поточний k –й стік. Якщо поточний стік відмічено як альтернативний, то GCRk – критичний шлях максимальної довжини серед критичних шляхів в альтернативні стоки, а решта критичних шляхів в альтернативні стоки не розглядаються.
3. Знайти в GA вершини, що не належать критичним шляхам, з яких ведуть дуги в вершини цих критичних шляхів. Ці дуги з GA видалити, а поточні стоки відмінити. Знайдені вершини призначити поточними стоками. Якщо такі вершини не знайдені, то перехід на п.5.
4. Знайти критичні шляхи, що ведуть з поточного джерела в поточні стоки. Граф GO зробити об`єднанню графа GO і цих критичних шляхів. Переход на п. 3.
5. В графі GA видалити всі дуги, що з`єднують вершини, що входять в граф GO, а також дуги, що ведуть в поточні стоки, в які були знайдені критичні шляхи в п.4. Вибрати наступне поточне джерело, як в п.1. Знайти стоки одержаного графа GA і вважати їх поточними. Якщо стоки вже належать також графу GO, то вони відмічаються як альтернативні.
6. Якщо не одержано пустий граф GA, то перейти на п.2., інакше кінець.
На рис. 2 показаний приклад побудови досконалого кістяка згідно з даним алгоритмом.
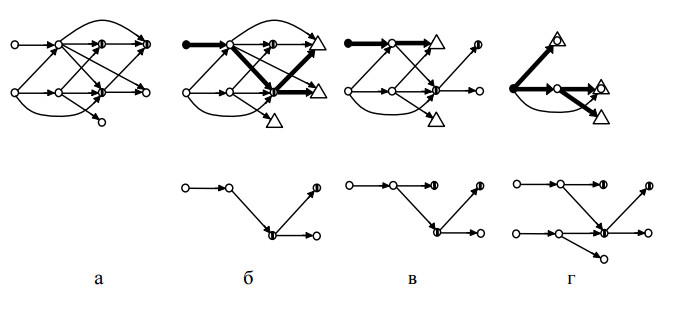
⚫− джерело, △− стік, △ з кружком − альтернативний стік, ①− вершина, в яку заходять критичні поперечні дуги, ➠− дуга з критичного шляху
Таким чином, в статті дано визначення досконалого кістяка алгоритма і доведено, що в нього входить критичний шлях алгоритма і показано, що за
допомогою його натуральним чином складається розклад за стратегією найскорішого призначення. На основі властивостей досконалого кістяка запропоновано алгоритм його побудови. Досконалий кістяк алгоритма дає змогу на його основі ефективним чином представити відомості про алгоритм, який відображається в апаратні або програмні засоби і прискорити пошук структурного рішення, або користувацької програми, що відповідає заданим критеріям ефективності, таким як мінімальні час виконання і апаратні витрати.
Список посилань
1. Bhattacharyya S. S., Leupers R., Marwedel P. Software Synthesis and Code Generation for Signal Processing Systems // IEEE Trans. on Circuits and Systems—II: Analog and Digital Signal Processing, − 2000. −V47. −№9. −p.849-875.
2. Каневский Ю.С., Овраменко С.Г., Сергиенко А.М. Отображение регулярных алгоритмов в структуры специализированных процессоров // Электрон. Моделирование.–2002.–Т.24.–№2.–С. 46-59.
3. Евстигнеев В.А. Применение теории графов в программировании / Под ред. А.П.Ершова. – М: Наука. –1985. –352 с.
4. Воеводин В.В. Математические модели и методы в параллельных процессорах. −М.: Наука, −1986. −296 с.
5. The Systhesis Approach to Digital System Design / P. Michelі, U. Lauther, P. Duzy −Eds. Kluwer Academic Pub. −1992. −415 p.