Вычисление квадрата
Анатолий Сергиенко
Функция возведения в квадрат — самая популярная функция. Школьник вспоминает о ней в связи с теоремой Пифагора, квадратным трехчленом, квадратурой круга. У инженера она ассоциируется с вычислением длины вектора, среднеквадратичного значения, полиномов.
Сейчас вычисление квадрата обычно выполняется умножением аргумента самого на себя. Но было время, когда в вычислительной технике умножение было в цене и возведение в квадрат выполнялось на специализированных устройствах — квадраторах. Даже само умножение иногда реализовалось как комбинация квадратов.
При реализации специализированных устройств на ПЛИС или заказных СБИС всегда хочется сэкономить оборудование или повысить быстродействие. В этом случае применение квадраторов может дать ощутимый эффект. Так, в последнее время широко распространяются методы шифрования, основанные на умножении и возведении в степень чисел с разрядностью 100,..,1000, таких как RSA. В устройствах шифрования по такому методу применение квадраторов может существенно уменьшить аппаратурные затраты и повысить быстродействие.
Операция умножения двух n — разрядных двоичных чисел дает 22n комбинаций результатов, а операция возведения в квадрат n — разрядного двоичного числа дает только 2n комбинаций результатов. Это означает, что ее реализация на умножителе значительно избыточна. На сокращении этой избыточности основана эффективность построения квадраторов.
Функцию квадрата, как и любую однозначную функцию можно реализовать таблично. Например, квадрат четырехразрядного аргумента вычисляет следующая функция, реализованная в виде процедуры:
procedure SQR4(signal x: in STD_LOGIC_VECTOR(3 downto 0);
signal y: out STD_LOGIC_VECTOR(7 downto 0)) is
begin
case X is
when "0000"=> Y<="00000000";
when "0001"=> Y<="00000001";
when "0010"=> Y<="00000100";
when "0011"=> Y<="00001001";
when "0100"=> Y<="00010000";
when "0101"=> Y<="00011001";
when "0110"=> Y<="00100100";
when "0111"=> Y<="00110001";
when "1000"=> Y<="01000000";
when "1001"=> Y<="01010001";
when "1010"=> Y<="01100100";
when "1011"=> Y<="01111001";
when "1100"=> Y<="10010000";
when "1101"=> Y<="10101001";
when "1110"=> Y<="11000100";
when "1111"=> Y<="11100001";
when others => null;
end case;
end procedure;
Эта процедура при ее вызове синтезируется в комбинационную схему, реализующую 8 логических функций от 4 аргументов, причем одна из функций равна нулю, а другая — повторяет младший разряд аргумента. Можно построить такую же процедуру вычисления квадрата и для большего числа разрядов аргумента. Но оборудование синтезированной схемы зависит от степени минимизации булевских функций компилятором-синтезатором и резко растет с ростом разрядности аргумента. Для разрядности аргумента 6, 7,… может оказаться более выгодным реализовать такую функцию в виде ПЗУ. Так, в ПЛИС Virtex квадратор для 8 — разрядного аргумента реализуется на одном блоке выделенной памяти (Block Select RAM). Однако, возникает некоторое неудобство, связанное с тем, что такое ПЗУ для каждой серии ПЛИС необходимо выполнять особенным образом. При этом информацию, записываемую в ПЗУ, необходимо оформлять отдельным файлом.
Чтобы построить функцию от аргумента с большим числом разрядов необходим другой конструктивный метод. Пусть аргумент x представлен своей старшей частью u и n — разрядной младшей частью v, т.е. x = u2n + v. Тогда его квадрат равен
y = (u2n + v)2 = u222n + 2u2nv + v2 ,
т.е. для реализации квадрата от 2n разрядного аргумента необходимо 2 квадратора от n — разрядного аргумента, n — разрядный умножитель и 2 сумматора. На рис.1 показана структура 8 — разрядного квадратора.
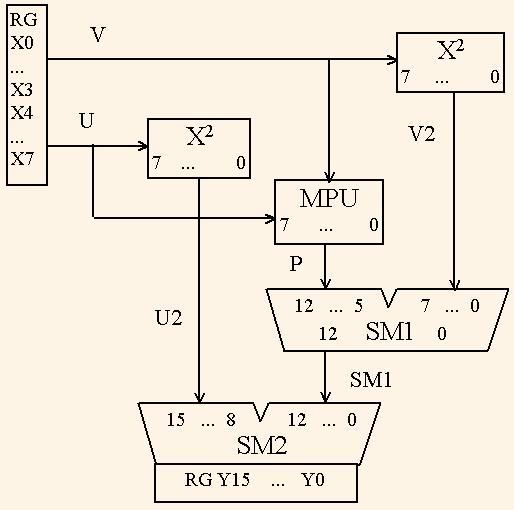
Эта структура описывается на VHDL следующим образом.
library IEEE;
use IEEE.STD_LOGIC_1164.all;
use IEEE.STD_LOGIC_ARITH.all;
entity SQR8 is port(CLK: in STD_LOGIC;
RST: in STD_LOGIC;
X:in STD_LOGIC_VECTOR(7 downto 0);
Y:out STD_LOGIC_VECTOR(15 downto 0));
end entity SQR8;
architecture STR of SQR8 is
signal U,V:STD_LOGIC_VECTOR(3 downto 0);
signal U2,V2,P:STD_LOGIC_VECTOR(7 downto 0);
signal SM1:STD_LOGIC_VECTOR(12 downto 0);
signal SM2:STD_LOGIC_VECTOR(15 downto 0);
procedure SQR4(signal x: in STD_LOGIC_VECTOR(3 downto 0);
signal y: out STD_LOGIC_VECTOR(7 downto 0)) is
. . .
begin
UV_REGISTER: process(CLK,RST,X)
begin
if RST='1' then
U<="0000";
V<="0000";
elsif CLK='1' and CLK'event then
U<=X(7 downto 4);
V<=X(3 downto 0);
end if;
end process;
SQR4(U,U2);
SQR4(V,V2);
P<=UNSIGNED(U)*UNSIGNED(V);
SM1<= UNSIGNED(P&"00000") + UNSIGNED(V2);
SM2<= UNSIGNED(U2&"00000000") + UNSIGNED(SM1);
Y_REGISTER: process(CLK,RST,SM2)
begin
if RST='1' then
Y<="0000000000000000";
elsif CLK='1' and CLK'event then
Y<=SM2;
end if;
end process;
end architecture STR;
Здесь функция " & " означает состыковку (конкатенацию) векторов , тип UNSIGNED означает подтип для STD_LOGIC_VECTOR , который применяется для аргументов арифметических функций сложения " + " и умножения " * " для передачи им информации, что с соответствующими векторами битов следует обращаться как с целыми числами в прямом коде без знака. Этот тип, функции " + " , " * " и функция преобразования типа UNSIGNED описаны в библиотеке IEEE.STD_LOGIC_ARITH.
Приведенный подход можно применить для большего числа разрядов аргумента. Например, если разбить аргумент на 3 группы разрядов, т.е.
x=a + b + c; то x2 = a2 + b2 + c2 +2ab + 2bc + 2ac.
При разбиении аргумента на n частей необходимо n квадраторов и n(n-1)/2 умножителей малой разрядности, а также соответствующее число сумматоров. При таком же разбиении аргументов для построения комбинационного умножителя потребуется n * n умножителей малой разрядности. Таким образом, оборудование квадратора приблизительно вдвое меньше, чем оборудование комбинационного умножителя такой же разрядности.
На основе n - разрядного квадратора несложно получить n+1 - разрядный квадратор. Разобьем n+1 - разрядный аргумент на 1 старший разряд a и число v из n младших разрядов, т.е.
x= a2n + v.
Тогда x2 = v2 при a=0 и x2 = 22n +2*2n*v + v2 при а=1.
На рис. 2 показана структура устройства n+1 = 5 - разрядного квадратора.
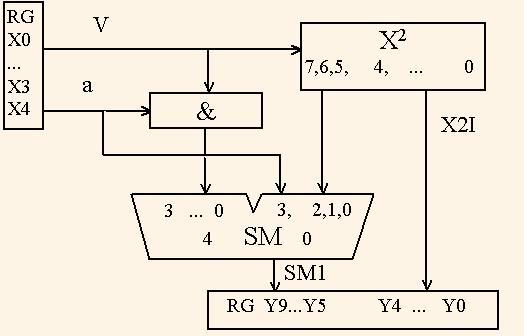
Подход к получению n+1 - разрядного квадратора можно применить рекурсивно. Т.е. 6 - разрядный квадратор строится аналогичным образом с использованием 5 - разрядного квадратора и так далее. В результате получим модель универсального квадратора, разрядность которого задается общей константой, т.е. константой generic. Такая модель описана на VHDL и приведена в приложении.
При синтезе квадраторов с различной структурой для ПЛИС серии Xilinx XC4000XLA с помощью системы Xilinx Foundation 2.1. получены устройcтва с различными аппаратурными затратами в количестве 4-х входовых логических таблиц (LUT) и быстродействием выраженным максимальной тактовой частотой, МГц. Параметры полученных устройств приведены в таблице.
| Разрядность | Квадратор на умножителе | Квадратор с разделением аргумента на 2 части | Квадратор с рекурсивными вычислениями | |||
| LUT | МГц | LUT | МГц | LUT | МГц | |
| 8 | 100 | 41.8 | 75 | 34.6 | 51 | 27.5 |
| 16 | 400 | 28.3 | -- | -- | 280 | 9.4 |
| 24 | 796 | 22.2 | -- | -- | 661 | 5.56 |
| 32 | 1584 | 19.1 | -- | -- | 1297 | 3.52 |
Взгляд на таблицу и модели квадраторов позволяет сделать следующие выводы.
- оборудование квадраторов значительно меньше, чем оборудование умножителя такой же разрядности;
- система Xilinx Foundation 2.1. синтезирует умножители гораздо эффективнее, чем предыдущие версии этой системы;
- производительность квадраторов гораздо слабее, чем у умножителей, что объясняется неглубокой оптимизацией схемы при ее синтезе ( задержка сравнима с задержкой умножителей, синтезируемых ранними версиями Foundation и М1). Однако, при использовании конвейеризации вычислений тактовую частоту можно неоднократно повысить, что гораздо труднее сделать для умножителя.
Приложение
--^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^
-- FILE: SQRN.VHD
-- PROJECT: Square Unit
-- AUTHOR: Anatoli Sergyienko
-- Email: aser@comsys.kpi.ua
--
-- FUNCTION: - calculating the square function
-- from the STD_LOGIC_VECTOR,
-- which represent the natural integer data.
-- CONSTRAINTS: the input data bit number is equal to
-- bit_num, where bit_num >4 is a generic value,
-- the output data bit number is equal to 2*bit_num,
-- respectively.
--^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^
library IEEE;
use IEEE.STD_LOGIC_1164.all;
use IEEE.STD_LOGIC_ARITH.all;
entity SQRN is generic(bit_num: integer:=8);
port(CLK: in STD_LOGIC;
RST: in STD_LOGIC;
X:in STD_LOGIC_VECTOR(bit_num-1 downto 0);
Y:out STD_LOGIC_VECTOR(bit_num*2-1 downto 0));
end entity SQRN;
architecture STR of SQRN is
signal XR:STD_LOGIC_VECTOR(bit_num-1 downto 0);
signal X0:STD_LOGIC_VECTOR(3 downto 0);
signal Y0:STD_LOGIC_VECTOR(7 downto 0);
signal X2:STD_LOGIC_VECTOR(2*bit_num-1 downto 0);
begin
X_REGISTER: process(CLK,RST,X)
begin
if RST='1' then
XR<=(others=>'0');
elsif CLK='1' and CLK'event then
XR<=X;
end if;
end process;
--initial square function
X0<=XR(3 downto 0);
SQR4:process(X0)
begin
case X0 is
when "0000"=> Y0<="00000000";
when "0001"=> Y0<="00000001";
when "0010"=> Y0<="00000100";
when "0011"=> Y0<="00001001";
when "0100"=> Y0<="00010000";
when "0101"=> Y0<="00011001";
when "0110"=> Y0<="00100100";
when "0111"=> Y0<="00110001";
when "1000"=> Y0<="01000000";
when "1001"=> Y0<="01010001";
when "1010"=> Y0<="01100100";
when "1011"=> Y0<="01111001";
when "1100"=> Y0<="10010000";
when "1101"=> Y0<="10101001";
when "1110"=> Y0<="11000100";
when "1111"=> Y0<="11100001";
when others => null;
end case;
end process;
--calculating the recursion
RECURSION:process(XR,Y0)is
variable X2I: STD_LOGIC_VECTOR(2*bit_num-1 downto 0);
variable V:STD_LOGIC_VECTOR(bit_num-1 downto 0);
variable SM1:STD_LOGIC_VECTOR(bit_num-1 downto 0);
variable a:STD_LOGIC;
variable i: integer;
begin
X2I:=(others=>'0');
X2I(7 downto 0):=Y0;
for i in 1 to bit_num-4 loop
V(i+2 downto 0):= XR(i+2 downto 0);
a:=XR(i+3);
if a='0' then
SM1(i+3 downto 0):= "00"&X2I(2*i+5 downto i+4);
else
SM1(i+3 downto 0):=
UNSIGNED('0'&a&X2I(2*i+5 downto i+4))
+UNSIGNED(V(i+2 downto 0));
end if;
X2I(2*i+7 downto i+4):=SM1(i+3 downto 0);
end loop;
X2<=X2I;
end process;
Y_REGISTER: process(CLK,RST,X2)
begin
if RST='1' then
Y<=(others=> '0');
elsif CLK='1' and CLK'event then
Y<=X2;
end if;
end process;
end architecture STR;