Простое устройство для решения задачи Пифагора
Анатолий Сергиенко
Задачи на теорему Пифагора каждый решал еще в школе. В технике эту задачу тоже надо решать и, нередко, миллионы раз в секунду. При управлении подвижными объектами( роботами, станками ) с ее помощью необходимо в реальном времени вычислять координаты точек в пространстве, и в таком случае эту задачу решают очень точно. В цифровой обработке сигналов задачу Пифагора называют вычислением модуля комплексного числа. Уровень шума ошибки вычислений не должен превосходить определенной границы, обеспечивая должное отношение сигнал-шум.
При распознавании образов, реализации алгоритма Витерби и других алгоритмов необходимо быстро и многократно вычислять расстояние между двумя точками в пространстве — так называемое Эвклидово расстояние. Это тоже сводится к решению задачи Пифагора.
Решение задачи Пифагора получают с помощью формулы: С = SQRT(A*A+B*B). С достаточно высокой точностью и квадрат числа, и квадратный корень можно вычислить на устройствах, описанных в заметкe Вычисление квадрата . Но для этого потребуются, возможно, чрезмерные аппаратурные затраты и длинная задержка вычислений. Следует отметить, что квадратный корень необходимо брать из числа с удвоенной разрядностью, а это в 4 раза сложнее, чем с одинарной разрядностью. Так, для обработки 12- разрядных данных получится схема из более чем 2000 LUT, с задержкой до 500 нс при реализации на Xilinx XS4000.
Во многих практических случаях достаточно невысокой точности вычислений, порядка 1-5%. Например, для оценки уровня сигнала, его визуального отображения, при вычислении дистанции до ближайших точек в пространстве, что необходимо при распознавании образов и т.д.
При этом не так важна относительная погрешность результатов, как расчеты в большом динамическом диапазоне, т.е. для относительно большой разрядности входных чисел. В этом случае в выигрыше будут устройства, реализующие прямую аппроксимацию формулы Пифагора.
Французский математик-механик Понселе был первым, кто предложил наилучшее линейное приближение формулы Пифагора в 1828 году.
Если A > 0, B > 0, A > B , то С ≈ 0.9605*A + 0.3978*B ,
а если A > 2B , то С ≈ 0.9859*A + 0.2327*B и т.д.
В первом случае обеспечивается точность 4%, а во втором — 1.4% [1].
Коэффициенты можно приближенно представить двоичным кодом как
0.9605 ≈ 0.11110110 и 0.3978 ≈ 0.0110110,
и можно представить суммой весов соответствующих разрядов, т.е.
0.11110110 = 1 — 1/16 +1/64 +1/128 и 0.0110110 = 1/4 + 1/8 +1/64 +1/128.
Вычисление результата С можно проще всего реализовать, заменив умножение на эти константы рядом сложений сдвинутых вправо операндов |A | и |B |, где |A | — абсолютное значение числа А со знаком. Количество сложений зависит от точности представления этих констант. Для вычислений с почти максимальной точностью формула будет выглядеть так:
С ≈ |A|-1/16*|A| +1/64*|A| +1/128*|A| +1/4*|B| +1/8*|B| +1/64*|B| +1/128*|B|,
где, например, коэффициент 1/16 взят из разложения множителя и умножение на него реализуется сдвигом вправо на 4 разряда.
Функция вычисления модуля комплексного числа A+jB на языке VHDL выглядит следующим образом.
function MAGN_APPROX(A,B: INTEGER) return INTEGER is variable Re,Im,Tmp,Magn: INTEGER; begin Re:=ABS(A); Im:=ABS(B); if Re < Im then Tmp:=Re; Re:=Im;Im:=Tmp; end if; Magn:=Re - Re/16+Re/64+Re/128+ Im/4 +Im/8+Im/64+Im/128; return Magn; end function;
В ней вначале вычисляются абсолютные значения операндов и переставляются операнды так, чтобы комплексная точка находилась в нулевом октанте, т.е. чтобы |A|>|B|. Затем вычисляется форула Понселе.
Таким образом, вычисляя эту функцию, мы аппроксимируем радиус окружности радиусом некоторой кривой замкнутой линии, показанной на рис.1.
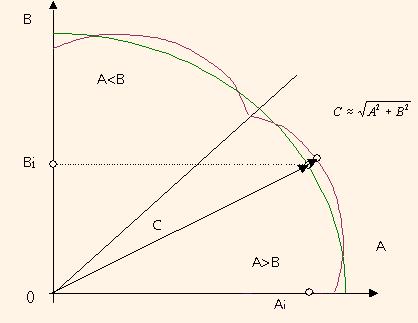
аппроксимираванная формулой Понселе (вишневая).
При реализации этого алгоритма в структуре можно использовать различное количество слагаемых в разложении коэффициентов. Естественно, это даст различные точность результатов и аппаратурные затраты полученных стрктур. Но среди этих структур можно выбрать оптимальную. Возможности VHDL обеспечивают несложную реализацию такой оптимизации структуры.
В таблице 1 приведены точностные параметры и некоторые результаты синтеза архитектуры MAGNITUDE синтезатором SYNPLIFY для ПЛИС серии XC4000XLA-0.7 для 12 - разрядных входных данных. Полученная модель устройства вычисления модуля комплексных чисел MAGNITUDE приведена в приложении 1.
Испытательный стенд для этого устройства приведен в приложении 2.
С помощью него и были получены параметры точности в таблице 1.
Таблица 1.
| № | Разложение коэффициентов функции Понселе | Макси- мальная ошибка Ммакс | Мат- ожи- дание М | Средне- квадра- тичное откло- нение q | Аппа- ратные затраты, LUT | Период вычис- лений, нс |
| 1 | 1 или 1/4 | -232 | -13 | 85 | 71 | 26 |
| 2 | 1 или 1/4 + 1/8 | 139 | 81 | 53 | 81 | 29 |
| 3 | 1 -1/16 и 1/4 + 1/8 | -147 | -33 | 47 | 93 | 29 |
| 4 | 1 -1/32 и 1/4 + 1/8 | -103 | 24 | 49 | 91 | 29 |
| 5 | 1-1/16 +1/64 и 1/4+1/8+1/64 | -89 | 6 | 48 | 106 | 32 |
| 6 | 1 -1/16 +1/64 +1/128 и 1/4 +1/8 +1/64 +1/128 |
82 | 25 | 48 | 122 | 33 |
Изучая таблицу 1, можно сделать следующие выводы.
Во-первых, то, что максимальная ошибка Ммакс действительно довольно точно выражается через матожидание и среднеквадратическое отклонение Ммакс =M±SQRT(3)*q, как было упомянуто в заметке О пользе округления .
Во-вторых, повышение точности разложения коэффициентов с определенной грани не ведет к повышению точности результатов, так как нельзя получить точность выше методической точности формулы Понселе.
В-третьих, при сравнении вариантов 5 и 6 оказывается, что более грубое разложение коэффициентов иногда может дать более высокую точность.
В-четвертых, варьирование разрядов в битовом разложении коэффициентов может дать дополнительное повышение точности, как в вариантах 3 и 4.
Результирующий вывод тот, что оптимальным по точности и аппаратным затратам является 4-й вариант, который и реализован в окончательной модели устройства.
В таблице 2 показаны некоторые результаты синтеза архитектуры MAGNITUDE синтезатором SYNPLIFY для ПЛИС серии XC4000XLA-0.7 для различной разрядности входных данных.
Таблица 2.
| Разрядность, n | 8 | 12 | 16 | 20 | 24 | 28 | 31 |
| Аппаратные затраты, LUT | 60 | 91 | 151 | 170 | 237 | 259 | 283 |
| Период вычислений, нс | 27 | 29 | 34 | 33 | 35 | 38 | 42 |
Синтезированная структура показана на рис. 2. На рисунке не показаны регистры, включенные на входе и выходе устройства для обеспечения высокой пропускной способности и повторяемости при реализации в ПЛИС. Устройство имеет 3 уровня логики.
Первый уровень составляют схемы получения абсолютного значения чисел А и В, второй уровень - схема перестановки с выбором максимального числа, третий уровень-четырехвходовый сумматор для вычисления формулы Понселе.
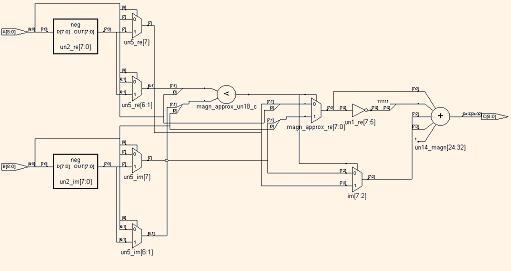
нарисованная с помощью Synplify.
Кое-что об испытательном стенде MAGN_TST
Он основан на сравнении результатов вычислений испытуемого устройства MAGNITUDE(MAGN_APPROX) с результатами эталонного устройства MAGNITUDEE(MAGN_EXACT).
Эталонное устройство, описанное в Приложении 2, вычисляет формулу Пифагора достаточно точно с плавающей запятой используя функцию SQRT пакета IEEE.math_real.
Исходные данные выдаются генератором синусов и косинусов, описанного в заметке Управляемый генератор синусоидальных сигналов . Таким образом, на входы двух устройств U2, U3 с одинаковыми интерфейсами, заданными компонентом MAGNITUDE, подается комплексный вектор М(cos+J*sin), конец которого описывает окружность радиусом М.
Процесс ERR вычисляет параметры ошибок вычислений равных разности результатов с выходов устройств U2, U3.
Варианты архитектур MAGNITUDE(MAGN_APPROX), MAGNITUDEE(MAGN_EXACT) назначаются экземлярам U2, U3 устройства MAGNITUDE с помощью конфигурации configuration MAGN_CONFIG of MAGN_TST.
Здесь показан пример того, как конфигурация позволяет привязать к экземплярам блоков с одинаковым названием их конкретные реализации в виде различных архитектур, даже если эти архитектуры уже странслированы в библиотеку проекта.
Устройство вычисляет функцию за 1 такт. Но это не всегда удобно. Часто реальная и мнимая части поступают по одной шине в четных и нечетных тактах. Когда-то автор получил авторское свидетельство на изобретение: "Устройство для вычисления функции √Y2 + X2 " А.С. СССР N 1541601, которое вычисляет формулу Понселе именно таким образом.
Так что в этом случае можно просто описать формулу этого изобретения на VHDL.
Как заключение, перечислим следующие выводы.
- Приведена вычислительная схема для вычисления модуля вектора или комплексного числа с минимальными аппаратурными затратами, высоким быстродействием и большим динамическим диапазоном.
- Минимальные затраты получены во-первых, благодаря линейной аппроксимации формулы Пифагора, во-вторых, путем замены умножения на коэффициенты операцией сложения сдвинутых слагаемых, в третьих, подбором оптимального числа сдвинутых слагаемых и количества разрядов сдвига.
- Ошибка вычислений составляет приблизительно 4%, но может быть уменьшена путем увеличения числа участков аппроксимации. Так, при разделении круга не на 8, а на 16 секторов, ошибку можно уменьшить до 1.5 %.
- Использование такого объекта VHDL, как конфигурация, позволяет привязать к экземплярам блоков с одинаковым названием их конкретные реализации в виде различных архитектур.
Литература
1. Люстерник Л.А., Червоненкис О.А., Янпольский А.Р. Справочная математическая библиотека. Математический анализ. Вычисление элементарных функций. -М.: Физматгиз. -1963. -247с.
Приложение 1.
--^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^
-- FILE: MAGNITUDE.VHD
-- PROJECT: Unit for complex number magnitude calculating
-- AUTHOR: Anatoli Sergyienko
-- Created: 09/02/00
-- Email: aser@comsys.kpi.ua
--
-- FUNCTION: synthesable model for
-- calculating the complex number magnitude
-- from the positive integer data.
-- CONSTRAINTS: the integer input data A,B is in range:
-- -2**n to 2**n-1,
-- where n<31 is generic, complex number (A+jB).
-- the output data is equal to SQRT(A*A* + B*B).
-- Mean error is +0.011, sigma is +-0.024.
--^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^
library IEEE;
use IEEE.std_logic_1164.all;
entity MAGNITUDE is
generic(n: integer:=11);
port (
CLK: in BIT;
RESET: in BIT;
A: in INTEGER range -2**n to 2**n-1;
B: in INTEGER range -2**n to 2**n-1;
C: inout INTEGER range 0 to -1+2**n+ 2**n
);
end MAGNITUDE;
architecture MAGN_APPROX of MAGNITUDE is
signal X,Y : integer range -2**n to 2**n-1;
function MAGN_APPROX(A,B: INTEGER) return INTEGER is
variable Re,Im,Tmp,t1,t2:Natural range 0 to 2**n-1;
variable Magn: NATURAL range 0 to 2**n+ 2**n-1;
begin
Re:=abs(A);
Im:=abs(B);
if Re < Im then
Tmp:=Re; Re:=Im; Im:=Tmp;--data swap
end if;
Magn:=Re - Re/32+ Im/4 +Im/8;
return Magn;
end function;
begin
process(CLK,RESET)
begin
if RESET='1' then
X<=0;
Y<=0;
C<=0;
elsif CLK='1' and CLK'event then
X<=A;
Y<=B;
C<=MAGN_APPROX(X,Y);
end if;
end process;
end MAGN_APPROX;
Приложение 2.
--^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^
-- FILE: MAGN_TST.VHD
-- PROJECT: Unit for complex number magnitude calculating
-- AUTHOR: Anatoli Sergyienko
-- Created: 09/02/00
-- Email: aser@comsys.kpi.ua
--
-- FUNCTION: - testbench for synthesable model for
-- calculating the complex number magnitude
-- from the positive integer data.
-- CONSTRAINTS: the integer input data A,B is in range:
-- -2**n to 2**n-1, where n<31 is
-- generic complex number (A+jB).
-- the output data is equal to SQRT(A*A* + B*B).
-- Mean error is +0.011, sigma is +-0.024.
--^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^
library IEEE;
use IEEE.std_logic_1164.all;
use IEEE.math_real.all;
entity MAGNITUDEE is
port (CLK: in BIT;
RESET: in BIT;
A: in INTEGER;
B: in INTEGER;
C: inout INTEGER);
end MAGNITUDEE;
architecture MAGN_EXACT of MAGNITUDEE is
signal Xi,Yi : integer ;
function MAGN_EXACT(A,B: INTEGER) return INTEGER is
variable Re,Im: REAL;
variable Magn: INTEGER;
begin
Re:=REAL(A);
Im:=REAL(B);
Magn:=INTEGER(ROUND(SQRT(Re*Re+Im*Im)));
return Magn;
end;
begin
process(CLK,RESET)
begin
if RESET='1' then
Xi<=0;
Yi<=0;
C<=0;
elsif CLK='1' and CLK'event then
Xi <=A;
Yi <=B;
C<= MAGN_EXACT(Xi,Yi);
end if;
end process;
end MAGN_EXACT;
Library IEEE;
use IEEE.math_real.all;
entity MAGN_TST is
end MAGN_TST;
architecture MAGN_TST of MAGN_TST is
signal CLK,RESET:BIT;
signal mean,SUM,QSUM,M_exact,M_approx: INTEGER;
signal error,SIN,COS,X,Y,FNUM,FDEN: INTEGER;
signal LMS:REAL ;
signal i: INTEGER:=-3;
component SINGEN is
Port(CLK : in BIT;
FNUM: in INTEGER;
FDEN: in INTEGER;
RESET: in BIT;
SIN : inout INTEGER;
COS : inout INTEGER);
end component SINGEN;
component MAGNITUDE is
port (
CLK: in BIT;
RESET: in BIT;
A: in INTEGER ;
B: in INTEGER ;
C: inout INTEGER
);
end component MAGNITUDE;
begin
CLK_GEN:process begin
CLK<=not CLK ;
wait for 50 ns;
end process;
INDEX_GEN:process (CLK) begin
if CLK='1' and CLK'event then
i<=i+1;
end if;
end process;
RESET<='1' after 0 ns, '0' after 50 ns;
FNUM<=0 after 0 ns, 1 after 50 ns;
FDEN<=0 after 0 ns, 1024 after 50 ns;
U1:SINGEN port map(CLK =>CLK,
FNUM=>FNUM,
FDEN=>FDEN,
RESET=>RESET,
SIN =>SIN,
COS =>COS);
X<=COS/16;
Y<=SIN/16;
U2: MAGNITUDE port map (
CLK=>CLK,
RESET=>RESET,
A=>X,
B=>Y,
C=>M_exact );
U3: MAGNITUDE port map (
CLK=>CLK,
RESET=>RESET,
A=>X,
B=>Y,
C=>M_approx );
error<= M_approx - M_exact;
err:process(CLK,i,RESET)
begin
if i=-1 or RESET ='1' then
SUM<=0; QSUM<=0; LMS<=0.0;
elsif CLK='1' and CLK'event
then SUM<=SUM+error;
if i =1024 then
Mean<=SUM/i;
end if;
if i >1024 then
QSUM<=QSUM+(error-Mean)*(error-Mean);
LMS<= SQRT(REAL(QSUM/(i-1024)));
end if;
end if ;
end process;
end MAGN_TST;
configuration MAGN_CONFIG of MAGN_TST is
for MAGN_TST
for U2 : MAGNITUDE
use entity MAGNITUDEE(MAGN_EXACT);
end for;
for U3 : MAGNITUDE
use entity MAGNITUDE(MAGN_APPROX);
end for;
end for;
end MAGN_CONFIG;