Реализация БИХ-фильтров на ПЛИС

A. M. Cepгиенко

1. Введение.

Фильтры с бесконечной импульсной характеристикой (БИХ) получили широкое распространение в цифровой обработке сигналов. Этому способствовали следующие факторы. БИХ-фильтры являются прямыми дискретными аналогами различных фильтров, используемых в аналоговой технике и переход от устройств обработки на аналоговых фильтрах к устройствам на БИХ-фильтрах понятный и несложный для специалистов. При одинаковом качестве передаточной характеристики БИХ-фильтры, как правило, имеют в несколько раз меньшую вычислительную сложность, чем фильтры с конечной импульсной характеристикой.

Наиболее часто БИХ-фильтры для обработки сигналов в реальном масштабе времени, реализуются на сигнальных микропроцессорах, а также в специализированных вычислителях, архитектура которых адаптирована к алгоритмам БИХ-фильтрации. Также для этих целей в последнее время применяются микропроцессоры общего применения с расширенной системой команд для приложений мультимедиа. БИХ-фильтры являются одним из первых применений ПЛИС в цифровой обработке сигналов [1]. Применение ПЛИС для реализации БИХ-фильтров имеет целый ряд преимуществ. Во многих случаях ПЛИС является единственно возможным решением для реализации этих фильтров.

В статье рассматриваются особенности алгоритмов БИХ-фильтрации, их эквивалентные преобразования, отображение в структуру фильтра, с учетом структурных особенностей ПЛИС. Также описывается разработанная библиотека параметризованных моделей БИХ-фильтров, предназначенных для реализации в ПЛИС, описанная на языке VHDL.

2. Алгоритмы БИХ-фильтрации.

Распространенный подход к синтезу БИХ-фильтров основан на преобразовании аналогового прототипа в его цифровой эквивалент. При этом дифференциальные уравнения, описывающие фильтрацию, заменяются на эквивалентные разностные уравнения, а преобразование Лапласа — на Z-преобразование.

БИХ-фильтрация заключается в решении разностного уравнения вида:

y_i = a₀x_i+a₁x_i-1+…+a_mx_i-m+b₁y_i-1+b₂y_i-2+…+b_ny_i-n ,  i = 1, 2,…, m≤n

соответствующего фильтру n-го порядка.

Ему соответствует передаточная функция в Z-плоскости вида:

   H_(Z) = (a₀+a₁z^-1+…+a_mz^-m)/(1-b₁z^-1-b₂z^-2-…-b_nz^-n)    (1)

   Фильтр порядка n можно представить в виде параллельного или последовательного соединения фильтров меньшего порядка. Наиболее часто используется последовательное соединение звеньев второго порядка, благодаря меньшему уровню внутренних шумов и лучшей устойчивости по сравнению с другими структурами фильтров.

Представление передаточной функции вида (1) формальным способом преобразуется в граф потоков данных (ГПД).

Например, передаточная функция H_(Z) = 1/(1-b₁z^-1-b₂z^-2)   соответствующая уравнению    y_i = x_i+b₁y_i-1+b₂y_i-2   (2)

преобразуется в ГПД на рис. 1.

ГПД кружок означает вершину операции сложения, треугольник означает вершину умножения на константу, а прямоугольник — задержку на один цикл, которая соответствует оператору z^-1.

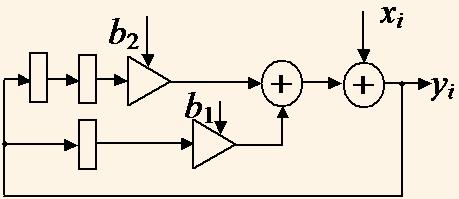
При подстановке в ГПД вместо операций сложения, умножения, задержки, соответственно блоков умножения, сумматоров и регистров получают структуру фильтра,которая выполняет вычисления с периодом τ = 1 такт. При этом минимальная длительность тактового интервала t_c определяется максимальной длиной пути в ГПД между смежными вершинами задержки.

Для ГПД на рис. 1 t_c = t_m+2t_A, где t_m, t_A — длительность выполнения умножения и сложения, соответственно.

Полученная таким единичным отображением структура может иметь максимальную производительность для заданного алгоритма за счет высоких аппаратурных затрат. На практике часто необходима фильтрация не с минимальным периодом, а с требуемым периодом t определяемым частотой дискретизации сигнала f_Q = 1/(τ*t_c) при минимальных аппаратурных затратах. Поэтому при синтезе структуры реального БИХ-фильтра необходимо выполнить более сложное отображение, чем единичное.

3. Преобразования графов потоков данных.

Перед отображением алгоритма и его ГПД в структуру фильтра с ним выполняют различные оптимизирующие функционально эквивалентные преобразования, такие, как ресинхронизация, развертка и опережающее вычисление, а также конвейеризация [2].

Ресинхронизацией является такая перестановка вершин задержки в ГПД, которая оставляет неизменной сумму вершин задержки в каждом из циклов графа. На рис. 2 показан один из возможных вариантов ресинхронизации ГПД на рис. 1.

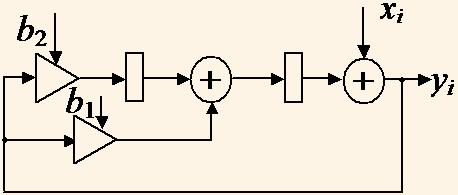
Для полученного ГПД количество вершин задержки уменьшено с трех до двух, т.е. с помощью ресинхронизации можно минимизировать количество регистров в фильтре. Также с помощью ресинхронизации выполняют в некоторых границах минимизацию длительности тактового интервала t_c.

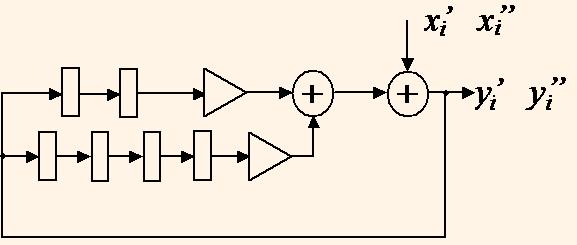
РГА представляет собой i-й период вычисления исходного алгоритма. Развернутым РГА с коэффициентом развертки J является РГА, который соответствует J соседним периодам алгоритма. Для РГА на рис. 1 развернутый с коэффициентом развертки J =2 РГА показан на рис. 3.

При отображении развернутого ГПД можно получить структуру БИХ-фильтра более эффективную, чем при отображении исходного РГА [2].

Сворачивание ГПД (folding) является преобразованием, противоположным развертке РГА. Например, если исходный ГПД представляет собой J несвязных одинаковых ГПД фильтра, то свернутый ГПД будет равен одному из исходных подграфов с увеличенным в J раз количеством вершин задержки.

При единичном отображении такого свернутого ГПД полученная структура будет выполнять J параллельных каналов фильтров с периодом τ = J тактов. На рис. 4 показан ГПД после сворачивания двух ГПД на рис. 1, а на рис. 5 — тот же ГПД после ресинхронизации.

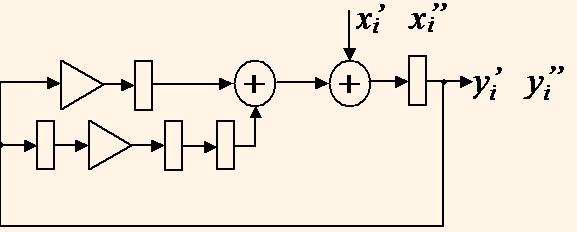
Нетрудно определить, что для ГПД на рис. 5 минимальная длительность тактового интервала равна t_c = max(t_m, 2t_a), что меньше, чем для ГПД до сворачивания.

Под опережающим вычислением понимают такое алгебраическое преобразование исходного алгоритма вычисления фильтра, которое в конечном счете приводит к минимизации длительности тактового интервала [2]. Нередко опережающее вычисление связано со значительным увеличением объема вычислений.

Например, объединив вычисление двух соседних итераций, уравнение (2) можно вычислять как:
y_i = x_i+b₁x_i-1+(b²₁+b₂)y_i-2+b₁b₂y_i-3, которому соответствует ГПД после ресинхронизации на рис. 6.

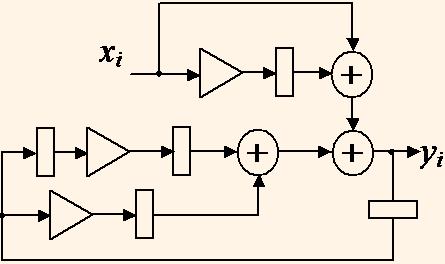
Для полученного ГПД минимальная длительность цикла равна t_c = max(t_m+2t_a), что меньше, чем для исходного ГПД.

При конвейеризации в ГПД добавляется некоторое число дополнительных вершин задержки и выполняется ресинхронизация таким образом, чтобы получить минимальную длительность тактового интервала t_c при условии неизменности исходного алгоритма. Особенно минимизируется t_c, если при этом операция умножения разделяется на несколько стадий. Конвейеризации ГПД посвящено много работ, например [3]. Нашедшая широкое применение при построении структур КИХ-фильтров, конвейеризация БИХ-фильтров имеет ограниченные возможности. Это связано с тем, что невозможно вставить дополнительные вершины задержки в цикл ГПД, не изменяя алгоритм. Поэтому можно только применить опережающее вычисление или свертывание ГПД, после которых увеличивается число вершин задержки в циклах ГПД. Поэтому строго ограниченное число вершин задержки в циклах ГПД является естественной границей роста пропускной способности БИХ-фильтров [4].

4. Отображение ГПД в структуру БИХ-фильтра.

Структурные модели устройств цифровой обработки сигналов, реализованные в виде специализированных СБИС можно разделить на такие группы, как, полученные единичным отображением, микропрограммируемые структуры, а также специализированные конвейеры [5].

Структуры, полученные единичным отображением, обладают высокой пропускной способностью. Однако, при использовании арифметики с параллельным представлением данных нередко аппаратурные затраты оказываются слишком высоки для реализации в ПЛИС. Исключением является отображение ГПД после его сворачивания, когда получается структура, в которой такие дорогие ресурсы, как умножители, оказываются разделенными [3]. С другой стороны, сворачивание ГПД можно трактовать, как один из способов неединичного отображения.

Очень часто единичное отображение выполняют в структуру с последовательной арифметикой, которая обеспечивает малые аппаратурные затраты, а также конвейеризованные вычисления, однако, частота дискретизации обрабатываемого сигнала должна быть равна f_Q = 1/(nt_c), где n — разрядность данных.

Структуры в виде микропрограммируемых БИХ-фильтров нашли широкое распространение в различных САПР специализированных СБИС [3, 6]. Модель вычислителя представляет собой набор ресурсов, таких как, умножители, сумматоры, блоки регистров, связанных общими шинами. Отображение ГПД заключается в последовательном выполнении стадий составления расписания (scheduling) и распределения ресурсов (allocation), на основании результатов которых автоматически составляется микропрограмма реализации алгоритма обработки сигналов. После нескольких итераций выполнения алгоритма отображения получают набор оптимизированных структур с различным вектором эффективности, который включает в себя период τ выполнения алгоритма и аппаратурные затраты в виде взвешенной суммы количества умножителей, сумматоров, регистров, шин. Среди полученного множества структур разработчик может выбрать требуемую структуру из соображений высокого отношения производительность-стоимость или заданного отношения тактовая частота — частота дискретизации.

Микропрограммируемая структурная модель имеет ограничения оптимизации аппаратуры, поскольку структурная оптимизация заключается только в варьировании числа ресурсов различного вида и поэтому не полностью может удовлетворить особенности элементной базы ПЛИС, как например, минимизация числа входов мультиплексоров, конвейеризация вычислений.

Структура специализированного конвейера, с одной стороны, наиболее адекватно отображает в себе особенности алгоритмов обработки сигналов, с другой стороны, ее локальность связей и конвейерность вычислений удовлетворяют особенности ПЛИС, благодаря чему можно достичь предельных тактовых частот ПЛИС. Чаще всего отображение в конвейерную структуру выполняют следующим образом. Граф конвейерной структуры получают путем сворачивания ГПД, затем определяют расписание выполнения операторов.

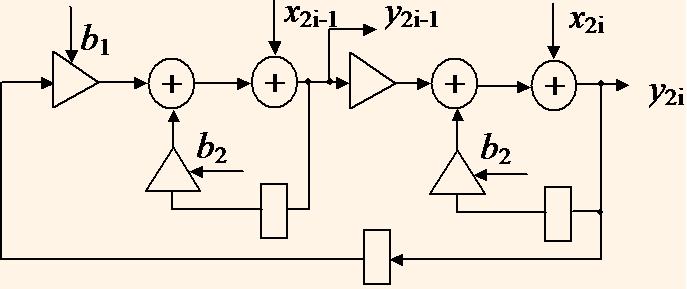
Сворачивание ГПД сводится к склеиванию в графе вершин операторов, которые должны выполняться в разделяемых ресурсах. При этом параллельные ветви заменяются одной ветвью с количеством вершин задержки, равным сумме вершин задержки в исходных ветвях, а на входах и выходах разделяемых ресурсов ставятся необходимые мультиплексоры — демультиплексоры [3]. На рис. 7 показан граф структуры БИХ-фильтра, полученный сворачиванием графа на рис. [1].

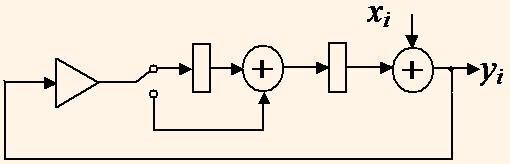
Полученная структура может выполнять БИХ-фильтрацию с частотой дискретизации f_Q = 1/(2(t_m+2t_a)), которая в τ = 2 раз меньше тактовой частоты и имеет всего один комбинационный умножитель.

Количество возможных вариантов сворачивания ГПД экспоненциально растет с увеличением сложности алгоритма, кроме того, ГПД предварительно необходимо оптимизировать путем ресинхронизации и конвейеризации. Вследствие этого получение оптимизированной структуры фильтра сворачиванием ГПД часто слишком трудоемко.

Известны работы по созданию методов отображения ГПД в конвейеризованные структуры, в которых поиск структурного решения выполняется направленно [3, 6].

В работе [7] предложен метод отображения ГПД в конвейерную структуру. Метод основан на представлении ГПД в многомерном пространстве с координатами времени, номера ресурса и типа операции, и его отображении в подпространства структур и времени. Поиск допустимого и оптимизированного отображения ведется формализованно с применением методов линейной алгебры и линейного программирования. Полученные структуры работают в конвейерном режиме с высокой загруженностью ресурсов и малым периодом тактовой частоты. При этом получение расписания выполнения операторов алгоритма с распределением им ресурсов выполняется почти одновременно, что сокращает сложность поиска оптимизированных решений. Структура фильтра полученная в [7] из ГПД на рис. 1 с применением этого метода показана на рис. 8.

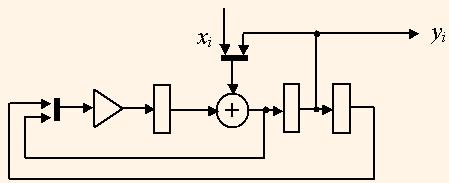
На рисунке толстой линией показаны мультиплексоры. Полученная структура может выполнять фильтрацию сигналов с частотой дискретизации f_Q = 1/(2t_m), т.е. с большей частотой, чем структура на рис. 7 при приблизительно равных аппаратурных затратах. Это также означает, что данная структура при условии t_m = 2t_a может иметь такую же пропускную способность как структура, полученная единичным отображением ГПД на рис. 1, 2, хотя и имеет на один умножитель и сумматор меньше.

При больших, чем 2 заданных значениях периода дискретизации τ метод позволяет оптимизировать ГПД путем ресинхронизации и конвейеризации одновременно с его отображением в структуру. При этом получаются структуры БИХ-фильтров с 2, 3 и более ступенями конвейера в комбинационных умножителях, что позволяет увеличивать частоту синхросигнала в ПЛИС до предельно возможных значений.

5. Параметрическая библиотека структур БИХ-фильтров.

Разработана библиотека моделей рекурсивных цифровых фильтров, которая представляет собой набор параметрических структур цифровых фильтров и предназначена для использования в проектировании систем цифровой обработки сигналов на базе FPGA. Для этого использован язык описания моделей VHDL .

Регулируемыми параметрами моделей являются следующие:

— nf — порядок фильтра, nf=2,3,…,10;

— τ — период вычислений тактов, τ = 1, …,10;

— коэффициенты звеньев фильтра: B₀, B₁ ,В₂ ,А₁, A₂..

Звено второго порядка вычисляется по алгоритму со следующим графом потоков данных (см. рис. 9) [8].

Причем, передаточная функция одного звена равна
                B₀+B₁Z^-1+B₂Z^-2
  H_(Z) =                                   ,
                1+A₁Z^-1+B₂Z^-2

   Bl₁ = (B₀+B₁-B₂ )/2; Bl₂ =( B₁+B₂-B₀)/2; Al₁ = (A₂-A₁-1)/2; Al₂ = (1-A₁-A₂ )/2.

Такая реализация звена второго порядка при условии, что полюсы передаточной функции H_(Z) находятся внутри окружности единичного радиуса, позволяет иметь устойчивые вычисления, причем абсолютная величина множителей не превышает единицы.

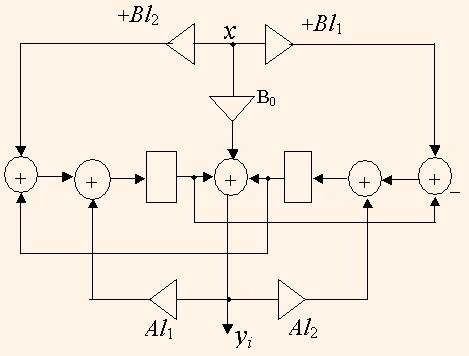
В структуре фильтра суммирование двух чисел выполняется за 1 такт, умножение двух чисел выполняется за два такта, причем период поступления данных на умножитель равен одному такту, т.е. умножение и сложение выполняются в конвейерном режиме. Поскольку значения коэффициентов известны заранее, умножение на них выполняется в специализированных умножителях на коэффициент. Эти умножители обладают малыми аппаратурными затратами и задержкой.

6. Заключение.

В статье рассмотрены особенности алгоритмов БИХ-фильтрации, их эквивалентные преобразования, отображение в структуру фильтра, с учетом структурных особенностей ПЛИС. Также описывается разработанная библиотека параметризованных моделей БИХ-фильтров, предназначенных для реализации в ПЛИС, описанная на языке VHDL. Алгоритмы БИХ-фильтрации отличаются наличием замкнутых циклов в их графах потоков данных. Поэтому они не могут быть непосредственно отображены в структуру с высоким уровнем конвейеризации, а следовательно, с высокой тактовой частотой. Функционально эквивалентные преобразования, такие, как ресинхронизация, развертка и опережающее вычисление, позволяют увеличить степень конвейеризации вычислений за счет увеличения периода τ поступления данных с 1 до 2, 3 и более тактов. Благодаря этому можно в 2-3 и более раз поднять тактовую частоту, и во столько же раз уменьшить аппаратные затраты. Этот вывод был подтвержден при реализации БИХ-фильтров на ПЛИС фирмы XILINX.

Литература

1. J. Isoaho, J. Pasawn, O. Vaino, H. Terhunen. DSP System Integration and Prototyping With FPGAs. J. VLSI Signal Processing, 1993, № 6, p. 155-172.
2. K.K. Parhi. Algorithm transformation techniques for concurrent processors. Proc. IEEE. 1989, V. 77, № 12, p. 1879-1895.
3. K.K. Parhi. C.Y. Wang, A. D. Brown. Synthesis of Control Cirсuits in Folded Pipelined DSP Architectures.
4. M. Renfors, Y. Nenvo. The maximum sampling rate of digital filters under hardware Speed constraints. IEEE Trans. Circuits Syst. 1981. V.CAS-28, N 3, p. 196-202.
5. H. Mann, F. Kathor, G. Hossens J. Vanhof. Methods of arichitectural synthesis for mapping signal processing algorithms into ASICs. Proc. IEEE. 1990, V. 78, № 2, p. 319-335.
6. The Systhesis Approach to Digital System Design / Ed.: P. Michel, U. Lauther, P. Duzy. Kluwer Academic Pub. 1992.
7. A. Sergyienko, A. Guzinski, Ju. Kanevski. A method for mapping unimodular loops into application specific parallel architectures. Proc. 2-nd Int. Conf. on Parallel Procesing and Applied mathematics. PPAM’97. Zacopane, Poland, Sept. 2-5, 1997, p. 362-371.
8. A. Fettweis, K. Meer Koetter. Suppression of parasitic oscillations in wave digital filters. IEEE Trans. Circuits Syst. 1975. V.CAS-22, N 3, p. 239-246.