Управляемый генератор синусоидальных сигналов
Анатолий Сергиенко
Симулятор VHDL — эффективное средство для моделирования устройств цифровой обработки сигналов (ЦОС). Подача дискретного синусоидального сигнала на вход устройства ЦОС — это наиболее привычный и надежный способ его проверки. Для получения синусоидального сигнала нужен генератор, модель которого, как правило отсутствует в библиотеках, поставляемых с симуляторами VHDL.
Наиболее простое решение — это построить таблицу M отсчетов одного периода синусоиды и считывать из нее данные по счетчику адреса, цикл работы которого определяет период синусоиды.
Сетка частот f = kfd /M, k=1,2,…,M/2 такого генератора синусоидального сигнала ограничена объемом таблицы, где fd — частота дискретизации.
Ее можно расширить путем интерполяции отсчетов, учета симметрии синусоиды, но тогда генератор становится громоздким.
Можно построить дискретный аналог аналогового генератора синусоиды, как это показано в заметке «Простой генератор синусоидального сигнала» (VHDLAB01).
Однако в таком генераторе, для каждой из частот необходимо вновь рассчитывать и вводить необходимые коэффициенты. Кроме того, амплитуда выходного сигнала зависит от частоты и округления коэффициентов, генератор не рассчитан на генерацию синусоиды с частотой выше fd /8.
Рассмотрим проектирование генератора синусоидальных сигналов с более высокими характеристиками точности, который можно применить в лаборатории как стандартный тестовый генератор.
Синусоидальный сигнал с частотой f часто представляют в виде вектора I единичной длины который вращается в комплексной плоскости со скоростью 2πf рад/сек.
Тогда его проекция на действительную ось равна Re(I)= cos(2πft), а на мнимую ось- Im(I)= sin(2πft).
Таким образом, дискретный генератор синусоидального сигнала можно представить как регистр вектора I, новое состояние которого I’ через период дискретизации равно старому I, повернутому на угол 2πf/fd , то есть I’ = Iexp(2πf/fd ).
Устройство для вращения комплексного вектора или просто вращатель можно выполнить в виде умножителя комплексных чисел. В результате получим следующие уравнения работы генератора.
cose(i) = cose(i-1)dcos - sine(i-1)dsin; sine(i) = cose(i-1)dsin + sine(i-1)dcos,
где I = cose(i) + jsine(i); cose(0)=1; sine(0)=0; exp(2πf/fd )= dcos + jdsin; i=1,2,…, ; j=√ (-1)
Операнды cose(i) и sine(i) при вычислениях необходимо в каждом цикле постоянно округлять до разрядности представления значений синуса и косинуса.
Вращающий коэффициент dcos + jdsin также представлен с точностью до округления. Вследствие ошибок округления возникает нестабильность вычислений: генерируемая синусоида будет затухать или увеличиваться по амплитуде вплоть до переполнения.
Для стабилизации амплитуды синусоиды в аналоговых генераторах, которые функционируют по аналогичному принципу применяется нелинейное звено в обратной связи. Коэффицитент передачи этого звена уменьшается при увеличении мощности сигнала, которая пропорциональна квадрату амплитуды комплексного вектора.
Это значение можно вычислить по формуле:
QAmplitude:= cose(i)*cose(i) + sine(i)*sine(i).
Тогда можно определить квадрат ошибки регулирования:
Delta:= (QAmplitude — 1) ,
который можно учесть для коррекции амплитуды комплексного вектора:
sine'(i) = sine(i)*(1-Ku*Delta);
cose'(i) = cose(i)*(1-Ku*Delta),
где Ku — коэффициент усиления ошибки, его оптимальное значение приблизительно равно 3/4 цены младшего разряда числа.
Граф потоков данных алгоритма генерации синусоиды и косинусоиды показан на рис.1.
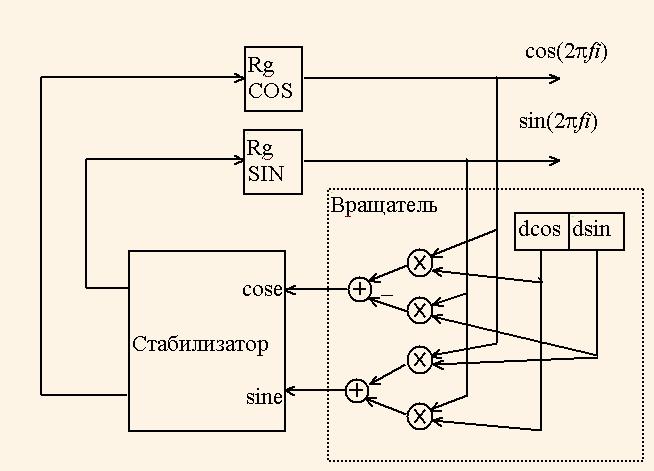
VHDL- программа, описывающая этот граф потоков данных приведена в приложении.
Стандарт языка VHDL требует представлять сигналы целыми числами или векторами. Поэтому в модели генератора все величины промасштабированы с масштабным коэффициентом 2-15.
Таким образом, выходные значения синуса и косинуса принимают значения 16-разрядных целых чисел в дополнительном коде.
Хотя VHDL- программа может оперировать с переменными, представленными с плавающей запятой, в реализациях языка отсутствуют библиотечные функции вычисления таких элементарных функций, как синус или косинус. Для удобства управления генератором в него введено вычисление этих функций. Функции синуса и косинуса аппроксимируются с помощью полиномов четвертой и пятой степени, соответственно.
Генератор вырабатывает сигнал синуса SIN и косинуса COS со стабильной амплитудой 32767+0-2. Частота синусоиды задается с помощью сигналов на входах FNUM и FDEN, причем частота выходного сигнала равна fs=fCLK*FNUM/FDEN, где fCLK =fd — частота синхросигнала.
Так, при fCLK=1 МГц, FDEN=1000, FNUM=20 генератор будет вырабатывать синусоиду с частотой 20 кГц, причем ее период будет состоять из FDEN/FNUM=50 отсчетов.
Таким образом, изменяя FDEN и FNUM можно задавать произвольную частоту синусоиды от 0 до fd , причем новая частота начинает вырабатываться как только изменится сигнал на входе FDEN или FNUM.
Следует отметить , что задаваеваемый период синусоиды, выраженный в числе тактов, не обязательно должен быть равен M/k ; k=1,2,…,M , M=2m как в генераторе на таблице синусов и может быть задан с произвольной точностью, которую может обеспечить полиномиальная аппроксимация коэффициентов dcos и dsin, а также диапазон представления целых чисел.
Типичное применение генератора — это построение свип-генератора синусоидального сигнала, по-другому называемого генератором качающейся частоты, который показан на рис. 2.
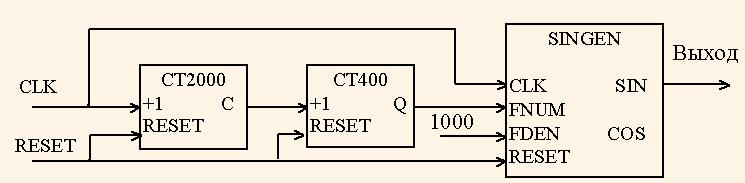
При частоте синхросерии 1 МГц этот свип-генератор последовательно вырабатывает серию синусоид с частотой от 0 до 400 кГц, с шагом 1 кГц, причем синусоида одной частоты состоит из 2000 отсчетов. Такой генератор удобно применять для тестирования цифровых фильтров, подавая его выходной сигнал на вход фильтра. Тогда амплитуда сигнала на выходе фильтра будет соответствовать его амплитудо-частотной характеристике.
Генератор синусоидальных сигналов имеет два выхода взаимно ортогональных сигналов — квадратурных сигналов. Такой генератор незаменим при построении моделей балансных модуляторов-демодуляторов, устройств гетеродинного переноса частоты, перестраиваемых остро настроенных узкополосных фильтров, анализаторов спектра.
Приложение
--^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^
-- FILE: SINGEN.VHD
-- PROJECT: Sine-Cosine Digital Generator
-- AUTHOR: Anatoli Sergyienko
-- Email: aser@comsys.kpi.ua
--
-- FUNCTION:
-- - the sine frequency Fs=fCLK*FNUM/FDEN,
-- where fCLK is frequency of the CLK-signal;
-- -Fs can be changed by outer source of signals FNUM,FDEN
-- in simulation process, for instance, as in sweep generator;
-- -usually FNUM/FDEN<0.5 according to Nyquist law;
-- -the magnitude of output signals SIN and COS
-- is equal to 32767+0-2;
-- -the phase error usually< 0.0005 rad.
--^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^
library IEEE;
use IEEE.Std_Logic_1164.all;
entity SINGEN is
Port(CLK : in BIT;
FNUM: in INTEGER;
FDEN: in INTEGER;
RESET: in BIT;
SIN : inout INTEGER;
COS : inout INTEGER);
end SINGEN;
architecture SINGEN_BEH of SINGEN is
--Polynomial approximation of the sine function
function SINU(x:in REAL) return REAL is
variable si: REAL;
begin
si:=(0.7853942*x)-(0.080714*x**3)+(0.0024271*x**5);
return si;
end;
--Polynomial approximation of the cosine function
function COSI(x:in REAL) return REAL is
variable cosi: REAL;
begin
cosi:= 0.99999-(0.3082451*x*x)+(0.0153718*x**4);
return cosi;
end ;
begin
GENERATOR: process(CLK,RESET,FNUM,FDEN)
variable x,dsin, dcos :REAL;
variable xi, dsi,dco,Delta,si,co,:INTEGER;
variable sine,cose, QAmplitude:INTEGER;
variable c,r: boolean;
begin
if RESET='1'then
SIN<=0;
COS<=32767;
elsif (FNUM'event)or(FDEN'event) then
x:=8.0*REAL(FNUM))/(REAL(FDEN));--x=1 equals Pi/4
xi:=INTEGER(x);
--deriving twiddle factors
case xi is --xi=0 --1st octant
when 0 => dsin:= SINU(x); dcos := COSI(x);
when 1 => dsin:= COSI(2.0-x); dcos := SINU(2.0-x);
when 2 => dsin:= COSI(x-2.0); dcos :=-SINU(x-2.0);
when 3 => dsin:= SINU(4.0-x); dcos :=-COSI(4.0-x);
when 4 => dsin:= -SINU(x-4.0); dcos :=-COSI(x-4.0);
when 5 => dsin:= -COSI(6.0-x); dcos :=-SINU(6.0-x);
when 6 => dsin:= -COSI(x-6.0); dcos := SINU(x-6.0);
when 7 => dsin:= -SINU(8.0-x); dcos := COSI(8.0-x);
when others => null;
end case ;
dsi:=INTEGER(dsin*32767.0);
dco:=INTEGER(dcos*32767.0);
--Main cycle
elsif CLK'event and (CLK='1') then
--twiddle
sine:=(SIN*dco+COS*dsi)/32768;
cose:=(COS*dco-SIN*dsi)/32768;
--stabilization
QAmplitude:=cose*cose+sine*sine;
Delta:=(QAmplitude-(32767*32767))/32768;
si:=(sine*(32768-(3*Delta/4)))/32768;
co:=(cose*(32768-(3*Delta/4)))/32768;
case si is
when 32768 => SIN<=32767;
when others =>SIN<=si;
end case;
case co is
when 32768 => COS<=32767;
when others =>COS<=co;
end case;
end if ;
end process GENERATOR;
end SINGEN;