Поведенческая модель процессора БПФ
(Из журнала ARGC & ARGV)
А.М.Сергиенко
Чтобы оценить возможности VHDL при исследовании алгоритмов цифровой обработки сигналов и начать на практике их использование, рассмотрим разработку и применение блока для вычисления БПФ.
Процедура БПФ широко используется в цифровой обработке сигналов для получения амплитудного и фазового спектров сигнала, а также для свертки длинных последовательностей отсчетов сигналов. В Matlab’е встроена процедура FFT, которая вычисляет БПФ для массива N комплексных данных с плавающей запятой. Если N равно степени двойки, то эта процедура выполняется довольно быстро. Результаты БПФ можно получить в виде графиков, выполнив процедуру PLOT.
В симуляторах VHDL обычно цифровые сигналы поступают, вырабатываются и наблюдаются в виде графиков, получаемых в процессе моделирования алгоритма. Но алгоритм БПФ предполагает, что данные поступают и выдаются сразу в виде массивов. Также многие другие алгоритмы обработки, как, например, решение систем уравнений, требуют аналогичного поступления данных. Поэтому целесообразно вычислять БПФ как цепочку процедур. Первая из них, называемая Gather_С, накапливает входной массив комплексных исходных данных. Вторая процедура – FFT – выполняет алгоритм БПФ, а заключительная процедура Scatter_С выдает результирующий массив в виде последовательности данных.
Указанные процедуры выполняются объектом FFTbeh. Этот объект можно вставлять в нужное место разрабатываемого проекта, как компонент, с целью измерить спектр интересующих сигналов или отобразить сигнал из временной области в частотную. Интерфейс этого объекта и перечень используемых стандартных библиотек выглядит так:
library IEEE;
use IEEE.std_logic_1164.all;
use IEEE.std_logic_ARITH.all;
use IEEE.MATH_REAL.all;
use IEEE.MATH_COMPLEX.all;
entity FFTbeh is
generic(
N:positive:=8; -- 2**N -длина преобразования
IDCT:natural:=0; -- 0- прямое, 1- обратное преобразование
PT:natural -- масштаб результата =2**PT
);
port (
CLK: in STD_LOGIC; -- синхросерия
RST: in STD_LOGIC; -- асинхронный сброс
START: in STD_LOGIC; -- начало накопления входного массива
EDIN: in STD_LOGIC; -- строб данных
DIN_RE: in integer; -- реальная часть данных
DIN_IM: in integer; -- мнимая часть данных
DOUT_RE: out integer:=0;-- реальная часть спектра
DOUT_IM: out integer:=0;-- мнимая часть спектра
NUM: out integer:=0; -- номер выходного отсчета
READY: out STD_LOGIC -- начало вывода результатов
);
end FFTbeh;
В библиотеках IEEE.MATH_REAL и IEEE.MATH_COMPLEX хранятся объявление типа комплексного данного, такие функции, как синус, косинус, квадратный корень, функции от комплексных аргументов и другие, которые применяются для вычисления БПФ.
Настроечная переменная N задает длину преобразования. При IDCT = 0 выполняется прямое преобразование, а при 1 – обратное. Переменная PT задает масштаб результата. Таким образом, преобразование равно
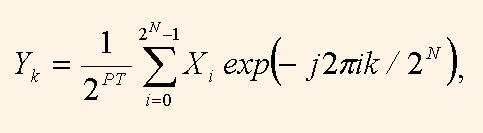
где Xi – отсчет входных комплексных данных: DIN_RE +j*DIN_IM, Yk – отсчет комплексного спектра: DOUT_RE +j*DOUT_IM.
По сигналу, приходящему в порт START, начинается накопление массива входных данных. Окончание вычислений БПФ указывается сигналом с выходного порта READY.
Выдаваемые отсчеты спектра сопровождаются номером отсчета NUM, по которому удобно находить значение частоты той или иной спектральной линии.
Различные блоки обработки сигналов целесообразно выполнить с интерфейсом, аналогичным интерфейсу объекта FFTbeh. Тогда их можно соединять между собой последовательно в соответствии с основным алгоритмом. При этом выходной порт READY одного блока соединяется с входным портом START следующего блока.
Сигнал на порте EDIN стробирует прием входных данных. В общем случае, этот сигнал разрешает работу блока в отдельных тактах. Это необходимо для моделирования и стыковки блоков, работающих с взаимно кратными периодами дискретизации. Например, с помощью блока FFTbeh можно определять узкополосный спектр после предварительной фильтрации полосовым фильтром и снижения частоты дискретизации в М раз. При этом сигнал EDIN должен иметь скважность 1:М.
Поведение объекта FFTbeh описано в архитектуре FFT_int. Для представления массивов данных в ней объявлены следующие типы массивов комплексных и действительных данных.
constant NN: integer:=2**N; -- длина преобразования type MEMOC is array (0 to NN) of complex; --комплексный массив type MEMOC_2 is array (0 to NN/2-1 ) of complex; type MEMOR is array (0 to NN-1) of real; --вещественный массив
В следующем тексте описана процедура, по которой накапливается массив входных комплексных данных.
procedure GATHER_C(signal CLK,START,EDIN:in std_logic;
signal DR,DI: in integer; --реальная и мнимая часть отсчетов входных данных
signal rdy: out std_logic; --сигнал готовности
signal datact: inout natural;--номер данного
signal RAM:out MEMOC) -- рабочий массив
is
variable TR,TI:real;
begin
wait until CLK= '1'; -- запуск процедуры по фронту CLK
if EDIN = '1' then -- проверка разрешения приема
TR:= real(DR); -- формирование комплексного данного
TI:= real(DI);
RAM(datact)<=(TR,TI); -- и запись его в массив
if datact < RAM'right then
datact<=datact+1; -- счетчик данных
end if;
if START='1' then
datact<=RAM'left; --обнуление счетчика данных
end if;
rdy<='0';
if datact =RAM'right-1 then
rdy<='1'; --массив готов
end if;
end if;
end procedure;
Такая процедура существенно отличается от процедур, к которым привыкло большинство программистов. В интерфейсе процедуры явно указываются не только тип данных, но и то, что они – сигналы, а также их направление: входные или выходные данные. При вызове процедуры ей не просто передается управление, а ее копия переписывается в модуль, который ее вызывает и там она связывается. Выполнение этой процедуры запускается по фронту синхросигнала CLK в операторе wait и останавливается после выполнения ее последнего оператора.
В данной процедуре при каждом ее запуске при EDIN = '1' в массив RAM по счетчику datact записывается очередная пара данных .
Процедура SCATTER_C выглядит следующим образом.
procedure SCATTER_C(signal CLK,START,EDIN:in std_logic;
pt:natural; -- масштаб результата
signal RAM:in MEMOC; -- входной массив
signal datact: inout natural; -- счетчик данных
signal rdy: out std_logic; -- конец вывода массива
signal DR,DI: out integer ) -- выходные данные
is
variable s:real:=real(2**pt); -- масштабный коэффициент
begin
wait until CLK='1';
if START='1' then
datact<=RAM'left;
elsif EDIN='1' then
RDY<='0';
DR<= integer(RAM2(datact).RE/s);
DI<= integer(RAM2(datact).IM/s);
if datact< RAM'right then
datact<=datact+1;
end if;
if datact=RAM'right-1 then
RDY<='1';
end if;
end if;
end procedure;
Эта процедура работает так же, как и предыдущая. Но наоборот, накопленные в массиве данные последовательно выдаются на ее выход (gather – собирать, scatter – разбрасывать).
Наконец, процедура, вычисляющая БПФ массива данных выглядит так:
procedure FFT(N:positive; -- размер преобразования =2**N
signal rdy:in std_logic; -- запуск преобразования
signal RAM_I: in MEMOC; -- входной массив данных
signal RAM_O:out MEMOC) -- выходной массив спектров
is
constant NN:positive:=2**N;
variable TWIDDLE:MEMOC_2; -- массив вращающих коэффициентов
variable RAM:MEMOC; -- рабочий массив
variable a,b,c,d,w: complex;
variable al:real;
variable base,itera,datact,twiddlect,twiddleinc: natural;
variable delta:integer:=1;
variable addrf: std_LOGIC_VECTOR(N-1 downto 0);
variable addri: std_LOGIC_VECTOR(N-1 downto 0);
begin
-- формування таблиці обертаючих коефіцієнтів
for i in 0 to NN/2-1 loop
al:= (MATH_PI*real(2*i))/real(NN);
if IDCT=0 then
TWIDDLE(i):=(COS(al),-SIN(al)); -- для прямого БПФ
else
TWIDDLE(i):=(COS(al), SIN(al)); -- для обратного БПФ
end if;
end loop;
loop -- основний цикл
wait until RDY='1'; -- начало БПФ
-- двоично-инверсная перестановка входных данных
addrf:=(others=>'0'); -- вектор адреса для прямого порядка
datact:=0;
for i in 1 to NN loop
for ind in 0 to N-1 loop -- инвертирование порядка бит
addri(ind):=addrf(N-1-ind); -- инверсный адрес
end loop;
RAM(CONV_INTEGER(unsigned(addri))):=RAM_I(CONV_INTEGER(unsigned(addrf)));
addrf:=unsigned(addrf)+1;
end loop;
-- собственно БПФ
itera:=0;
delta:=1;
twiddleinc:=0;
for itera in 1 to N loop --начало итерации
base:=0;
twiddlect:=0;
for butterfly in 0 to NN/2 - 1 loop
a:=RAM(base); -- начало базовой операции
base:=base+delta;
b:=RAM(base);
w:=TWIDDLE(twiddlect);
c:=a + b * w; -- собственно бабочка
d:=a - b * w;
RAM(base-delta):=c;
RAM(base):=d; -- конец базовой операции
-- модификация параметров базовой операции
base:= base + delta;
if base >= NN then
base:=base-NN+1;
twiddlect:=twiddlect+twiddleinc;
end if;
end loop; -- конец итерации
-- модификация параметров итерации
delta:=delta*2;
if itera=1 then
twiddleinc:=NN/4;
else
twiddleinc:=twiddleinc/2;
end if;
end loop;
RAM_O<=RAM; -- результаты БПФ
end loop;
end procedure;
Здесь выполняется известный алгоритм БПФ по основанию 2 с прореживанием по времени с замещением данных [5]. Процедура имеет два участка: первый из них выполняется однократно в начале моделирования, а второй – собственно БПФ - выполняется периодически. При выполнении первого участка формируется таблица вращающих коэффициентов, размер которой равен длине преобразования и которая затем используется алгоритмом БПФ.
Второй участок представляет собой бесконечный цикл. Цикл запускается, как только готов массив исходных данных, подготавливаемый процедурой GATHER_C. После запуска данные переписываются из входного массива в рабочий массив. При этом выполняется двоичная инверсия адресов записи. Следует отметить простую и оригинальную возможность двоичной инверсии адреса, которую предоставляет язык VHDL. Адрес представляется битовым вектором и биты в нем переставляются в инверсном порядке непосредственно. В обычных языках для этого необходимо выполнить сложный и не всегда очевидный алгоритм.
Как и все алгоритмы БПФ, данный алгоритм представляет собой гнездо циклов. Во внутреннем цикле выполняются базовые операции БПФ, а внешний цикл образован N итерациями алгоритма БПФ.
Исполнительная часть архитектуры содержит вызовы описанных выше процедур:
begin
INPUT:GATHER_C(CLK,START,EDIN,
DR=>DIN_Re,DI=>DIN_IM,
rdy=>idatardy,datact=>datact_I,RAM=>RAM1);
SPECTRUM:FFT(N,idatardy,RAM_I=>RAM1,RAM_O=>RAM2);
OUTPUT: SCATTER_C(CLK,idatardy,EDIN,PT,
RAM=>RAM2,DATACT=>datact_o,
rdy=>rdy,DR=>DOUT_RE,DI=>DOUT_IM);
DEL:process(CLK) begin
if CLK='1' and CLK'event and EDIN='1' then
READY<=idatardy;
NUM<= datact_o;
end if;
end process;
end FFT_int;
Для понимания исполнения программы следует напомнить, что параллельный вызов процедуры, в которой применяется оператор wait, эквивалентен оператору процесса, тело которого состоит из тела процедуры. Таким образом, все три процедуры, как и эквивалентные им процессы, исполняются параллельно в некотором конвейерном режиме. При этом данные и управление передаются от процедуры к процедуре как между ступенями конвейера. В результате, объект FFTbeh обрабатывает непрерывный поток данных, сегментируя его на блоки длиной 2**N.
Процесс DEL выполняет задержку сигнала готовности READY и потока номеров NUM отсчетов результата на один такт, чтобы они соответствовали выходным отсчетам сигналов DOUT_RE и DOUT_IM .
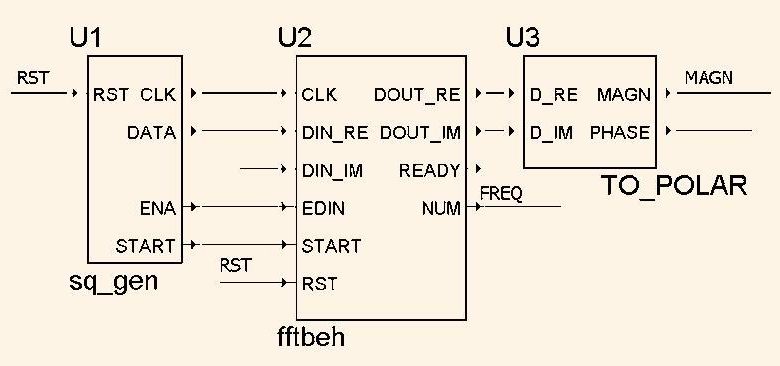
Рассмотрим простой пример применения объекта FFTbeh для измерения спектра сигнала, выдаваемого генератором прямоугольных импульсов. Графическая программа, подготовленная в среде Aldec Active HDL, показана на рис.1.
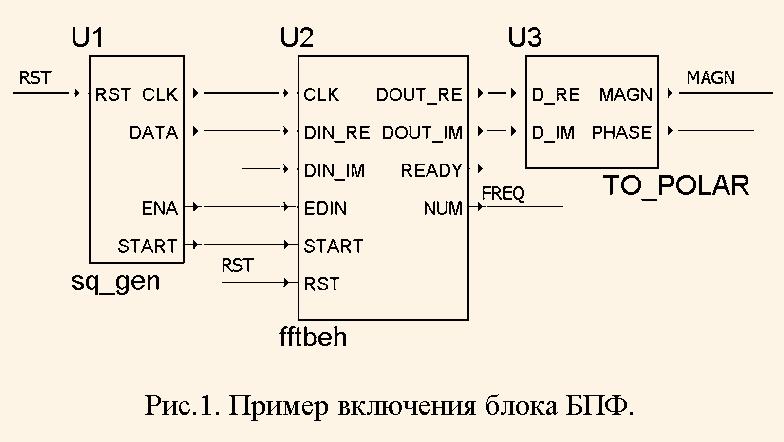
Здесь компонент U1 представляет собой программируемый генератор прямоугольных импульсов DATA с выдачей синхросерии CLK, сигналов START и ENA. Компонент U2 - это описанный выше блок БПФ, а U3 – преобразователь комплексных чисел из прямоугольной системы координат в полярную.
VHDL – симулятор может выдавать на экран целочисленный сигнал в виде графика. Как привило, этот график с осями представлен с помощью средств векторной графики. Поэтому его можно выделить и через "карман" ПК переместить, например, в редактор текста, такой как MS Word. На рис.2. показаны графики сигналов, сгенерировнных при моделировании модели на рис.1. В этом эксперименте определялся спектр прямоугольного импульса с периодом 256 тактов и длительностью 10 тактов с помощью БПФ длиной 256 отсчетов.
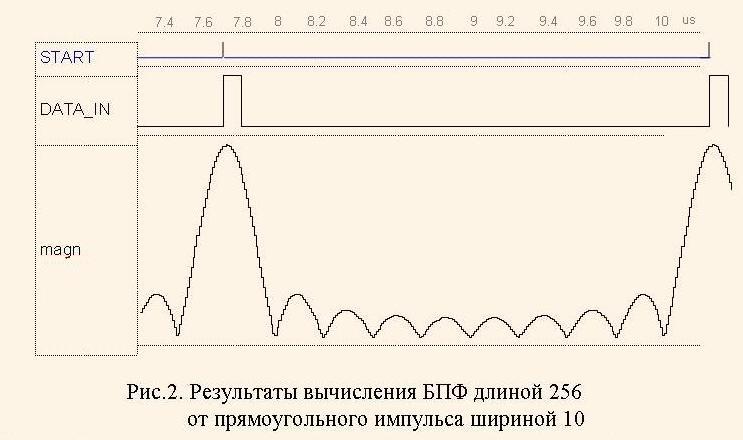
Как видим, предложенный блок БПФ эффективен в использовании. Получаемые с помощью его спектра графики удобны как для восприятия, так и для документирования и сохранения. Причем скорость вывода графиков и быстродействие системы при их изучении (перемещение, изменение масштаба, измерение в заданных точках) многократно выше, чем при использовании Matlab'a.
При необходимости, описанный блок БПФ можно без особого труда доработать для того, чтобы входные и выходные данные были с плавающей запятой. Такая доработка сводится лишь к замене целого типа данных на тип real.