Анализ цифровых фильтров с помощью VHDL. Фазовые и маскирующие фильтры
А.М. СЕРГИЕНКО
z-преобразование и передаточная функция
z-преобразование широко используется в цифровой обработке сигналов (ЦОС) потому, что сигнал вида x(n) = zn является собственной функцией для линейной системы, которая инвариантна к сдвигу. То, что функция является собственной для системы, означает, что после обработки сигнала, который имеет форму этой функции, получим сигнал, который имеет такую же форму, но является задержанным во времени и имеет другую амплитуду. Покажем, что zn является собственной функцией для системы, которая описывается импульсной реакцией h(k). Если такой сигнал подать на вход системы, то на выходе получим (согласно свойствам линейной системы инвариантной к сдвигу) исходный сигнал
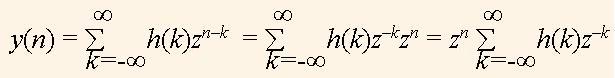 (1)
(1)
Итак, видим, что функция zn прошла неизменной на выход системы. Согласно (1), передаточная функция системы равна
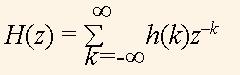 (2)
(2)
Так же, как и z, функция H(z) является комплексной функцией с амплитудой |H(z)| и фазой arg(H(z)). Функция H(z) имеет два множества особых точек. Первое множество — это такие точки q1,…,qM для которых |H(qі)| = 0 и потому называются нулями функции H(z). Второе множество — это такие точки r1,…,rN, для которых |H(rі)| =∞ и потому они называются полюсами, функции H(z).
Чтобы найти нули и полюса H(z), выражение (2) превращают в дробь с положительными степенями при z. Если M — N = L, то числитель H(z) умножают на zМ,а знаменатель — на zN. После этого получают дробь
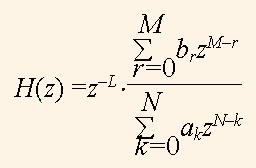 (3)
(3)
числитель и знаменатель которой представлены полиномами с положительными степенями при z, где a0 = 1, множитель z-L представляет собой задержку на L тактов и, как правило, может быть устранен из рассмотрения. Эти полиномы приравнивают к нулю и находят корни этих уравнений q1,…,qM и r1,…,rN, соответственно. Имея множества нулей и полюсов, функцию H(z) можно выразить через них с помощью формулы
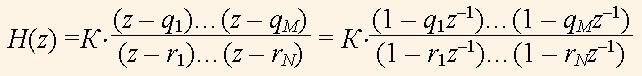 (4)
(4)
где К — коэффициент усиления системы. Итак, множества нулей и полюсов определяют передаточную функцию системы.
Нули и полюса передаточной функции
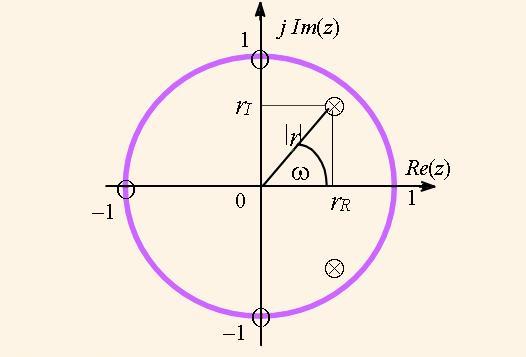
Графически нули и полюса изображают как точки на комплексной плоскости в виде кружочков и крестиков, соответственно. На рис. 1 показан пример размещения нулей и полюсов некоторого фильтра низких частот. Нуль или полюс, как корень уравнения, вычисляют как пару реального и мнимого чисел: r = rR + jrI . Для удобства корни представляют в полярных координатах парой амплитуды |r| и фазы ω: r = |r|е-jω . При этом фаза ω отвечает определенной частоте сигнала или передаточной функции. Амплитуда полюса, как правило, не превышает единицы, т.е. |r| < 1 , а количество полюсов с ненулевыми мнимыми координатами всегда парное.
Амплитудно-Частотная характеристика
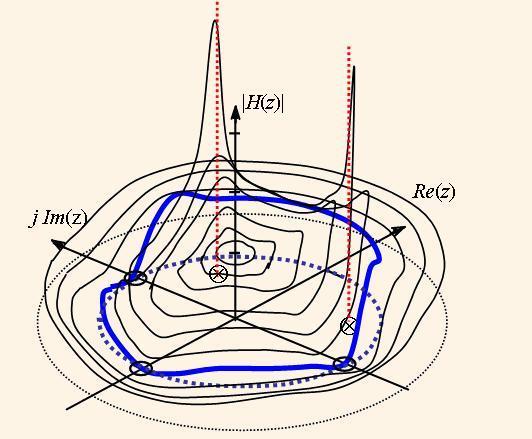
Модуль передаточной функции |H(z)| в трехмерном пространстве можно представить как бесконечную упруго растягивающуюся мембрану, которая натянута над комплексной плоскостью на единичной высоте. Точки мембраны, отвечающие нулям функции, притянуты к комплексной плоскости, а точки, обозначающие полюса, оттянуты вверх к бесконечности. Если на мембране изобразить концентрические круги, то после ее деформации согласно размещению нулей и полюсов как на рис. 1, получим изображение, как на рис. 2. Толстая линия на поверхности |H(z)| (рис. 2) отображается на комплексную плоскость как окружность с единичным радиусом. Она строится при
![]() (5)
(5)
При подстановке последовательности е-jω в H(z) получим дискретное преобразование Фурье, а при подстановке в (2) или (3) — передаточную функцию
|H(ω)| = |H(е-jω)|, (6)
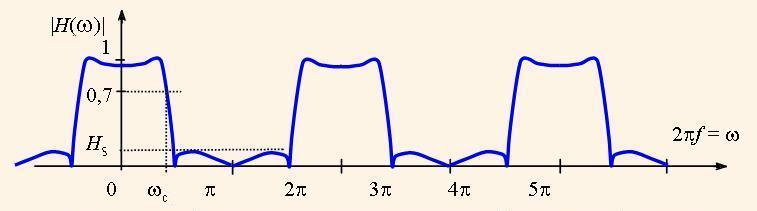
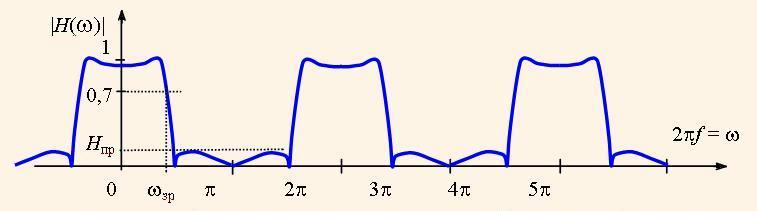
т.е. зависимость коэффициента передачи системы от частоты ω . Эту функцию называют амплитудно-частотной характеристикой (АЧХ) системы. При этом кривая, которая на рис. 2 размещена на цилиндре единичного радиуса с осью о|H(z)|, раскручивается на плоскости графика АЧХ в виде бесконечной периодической кривой с периодом 2π, как на рис. 3.
Для удобства ось частот графика АЧХ нормируют делением аргумента на 2π, поэтому единица на этой оси отвечает частоте дискретизации сигнала. Аналогично АЧХ, вычисляют фазо-частотную функцию (ФЧХ) системы
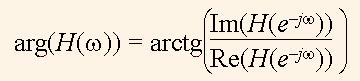 (7)
(7)
Для АЧХ цифровых фильтров договорено, что в полосе пропускания АЧХ имеет уровень не ниже √0,5 ≈ 0,7. Это означает, что в этой полосе мощность фильтрованного сигнала не снижается меньше, чем на уровень 0,5 от номинальной мощности. Соответствующая частота границы полосы называется частотой среза (ωзр на рис. 3). Максимальный уровень фильтрованного сигнала в полосе непропускания называется уровнем подавления фильтра (Нпр на рис. 3).
Из-за того, что большинство систем ЦОС являются системами с последовательно соединёнными блоками, удобно представлять АЧХ в логарифмическом масштабе, т.е. H(ω) = 20*lg|H(е-jωn)|. Тогда результирующая АЧХ системы равняется сумме АЧХ ее составляющих. При этом отсчет уровней АЧХ ведут в децибелах. Например, уровню 1 отвечает 0 дб, уровню 0,7 -уровень 3дб., уровню 0,1 -уровень 20 дб.
Фазовые фильтры
Дальше будут исследоваться характеристики передаточной функции
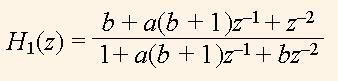 (8)
(8)
и других передаточных функций на ее основе. H1(z) отвечает фазовому фильтру, нули и полюса которого показаны на рис. 4. Нули и полюса функции (8) имеют одинаковый угол ω. Если модуль ее полюса r, то модуль нуля равняется обратной величине, т.е. 1/r. Следовательно, нули полностью компенсируют влияние полюсов и поэтому АЧХ равняется 1 во всем диапазоне частот.
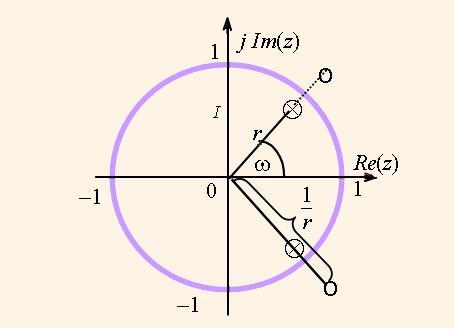
Положение полюсов и нулей определяется коэффициентами a,b, причем
a = — cos(ω); b = r2. (9)
Фазовый фильтр не изменяет амплитуды сигнала, но искажает его фазу. Причем, чем ближе параметр b к единице, тем резче искажение фазы на частоте ω. Если соединить параллельно два фазовых фильтра с характеристиками H1(z), H2(z), т.е.:
H3(z) =(H1(z) + H2(z))/2, (10)
то в их общей передаточной характеристике H3(z) нули перестают компенсировать полюса. Оба канала H1(z), H2(z) пропускают два сигнала без изменения их амплитуд. Но на частотах, где разность фаз равна π, 3π,…, сигналы компенсируют друг друга и результирующий сигнал явдяется нулевым. Наоборот, на частотах, где разность фаз 0,2π, 4π,…, этот сигнал остается без изменений. Благодаря этому, в результирующей АЧХ |H(ω)| появляются полосы пропускания и непропускания.
Фильтры с кратными задержками и маскирующие фильтры
В любой линейной системе, инвариантной к сдвигу, можно увеличить каждую задержку в k раз. Тогда вместо передаточной функции H(z) рассматривается функция с кратными задержками H(zk). Эффект такого увеличения задержек состоит в том, что масштаб графиков АЧХ, ФЧХ вдоль оси частот уменьшается в k раз.
Пусть k=2, , тогда на графике на рис. 3 нужно заменить отсчеты π на π/2, 2π на πи т.д. В результате, количество полос пропускания и непропускания в частотной области, которая рассматривается, удваивается.
Пусть имеем H4(z) = H3(zk). Если АЧХ |H4(ω)| имеет несколько полос пропускания, то рабочую полосу можно выделить с помощью маскирующего фильтра HМ(z), соединенного последовательно с фильтром, который реализует H4(z). Т.е. результирующая функция
H(z) = H4(z)*HМ(z) (11)
Для этого АЧХ маскирующего фильтра должна иметь полосы непропускания в тех диапазонах частот, где находятся полосы пропускания в АЧХ |H4(ω)|, которые необходимо подавить.
VHDL-Функции для анализа передаточных функций
Для вычисления передаточных функций нужно использовать пакеты ІEEE.MATH_REAL и ІEEE.MATH_COMPLEX. В последнем пакете определены типы, константы и функции, которые оперируют с комплексными данными.
Для вычисления передаточных функций разработаны ряд функций с использованием пакетов ІEEE.MATH_REAL и ІEEE.MATH_COMPLEX. Вычисление последовательности zn выполняется с использованием следующих функций, которые перезагружают друг друга
--число Z радиусом MAG в степени угла j*fі
function Z(mag,fi:real) return COMPLEX_POLAR is
begin
return mag*exp(COMPLEX_TO_POLAR(MATH_CBASE_J)*(fi));
end Z;
--число Z радиусом 1 в степени угла j*fі
function Z(fi:real) return COMPLEX_POLAR is
begin
return exp(COMPLEX_TO_POLAR(MATH_CBASE_J)*(fi));
end Z;
Следующая функция вычисляет H1(z) по формуле (8), но для положительных степеней z, т.е. с учетом (3). Она необходима для сканирования пространства |H1(z)| при поиске нулей и полюсов, когда устанавливается разная величина mag амплитуды и фазы fі комплексного вектора z. Также она используется для расчетов АЧХ и ФЧХ.
вычисляет (bZ2+а(b+1)Z+1)/(Z2+c(b+1)Z+b)
function Allpass2(b,a: real; --коэффициенты
mag, fi: real) -- амплитуда, угол для z
return COMPLEX_POLAR is variable tn,td: COMPLEX_POLAR;
begin
td:=COMPLEX_TO_POLAR(COMPLEX'(b,0.0))
+a*(b+1.0)*Z(mag,fi) + Z(mag**2,2.0*fi);
tn:=COMPLEX_TO_POLAR(COMPLEX'(1.0,0.0))
+a*(b+1.0)*Z(mag,fi) + b*Z(mag**2,2.0*fi);
return tn/td ;
end Allpass2;
Следующая функция вычисляет H1(z2) (8) для отрицательных степеней z с единичной амплитудой, т.е. она вычисляет H1(ω), где ω = fi . Поэтому она используется лишь для расчетов АЧХ и ФЧХ.
function Allpass2x2(b,c:real; fi:real) return COMPLEX_POLAR is variable tn,td: COMPLEX_POLAR; begin tn:=COMPLEX_TO_POLAR(COMPLEX'(b,0.0)) +c*(b+1.0)*Z(-2.0*fi) + Z(-4.0*fi); td:=COMPLEX_TO_POLAR(COMPLEX'(1.0,0.0)) +c*(b+1.0)*Z(-2.0*fi) + b*Z(-4.0*fi); return tn/td ; end Allpass2x2;
Для сканирования пространства |H1(z)| используется следующий фрагмент VHDL-программы.
signal clk:bit;
signal m,ph:real:=0.0;
signal a,b,logm,phase,mag:real:=0.0;
begin
clk<=not clk after 5ns; --генератор синхросигналов
process(CLK)
variable p,phas:real:=0.0;
variable Hz: COMPLEX_POLAR;
begin
a<=-0.5; b<=0.64; -- параметры H(z)
if clk='1' and clk'event then
phas:= phas+0.001; -- счетчик фазы (частоты)
p:=phas*MATH_PI*2.0; -- нормированная фаза
m<= trunc(phas)*0.1+0.1; -- амплитуда Z
ph<=phas; -- сигнал фазы
end if;
Hz:=Allpass2(b,a,m,p); --собственно H(z)
mag<=abs(Hz); -- амплитуда H(z)
phase<=Hz.ARG; -- фаза H(z)
logm<=20.0*log10(abs(Hz)); -- H(z) в децибелах
end process;
Исследование фазовых фильтров с помощью VHDL
Исследуем функцию H1(z) с помощью программы на VHDL, которая строит графики |H1(z)| для разных значений |z| чтобы экспериментально определить положение нулей и полюсов функции (7). Пусть задано a = -0.5, b = 0.64. Тогда
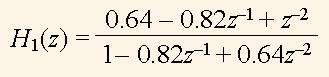 (12)
(12)
После запуска программы на моделирование в системе Aldec ActіveHDL получен график |H1(z)| (рис. 5), в котором на нескольких интервалах, обозначенных m, размещены кривые |H1(m,ph)|, где m - длина (причем m = 0.1, 0.2,...), ph - нормированный угол (фаза, частота) вектора z, полный оборот вектора z происходит когда ph - целое число. Первая половина |H1(m,ph)| - для m = 0.1,...0.9, а вторая половина - для m = 1.0,...1.9. Таким образом, каждый интервал отвечает замкнутой кривой, как на рис. 4. Там же аналогично показан график arg(H1(z)) для m = 0.6,...1.1.
Анализ графиков на рис. 5 показывает, что полюса функции H1(z) имеют фазу ± 2π*ph = ± 2π*0.1645 = ± 1.0336 и находятся в точках r1 = 0.8 ∠1.0336 и r2 = 0.8 ∠-1.0336. Нули функции H1(z) имеют такую же фазу и равны q1 = 1.3 ∠1.0336, q2 = 1.3∠-1.0336. Нужно отметить, что -cos(1.0336) = -0.512 ≈ а, 1/0.8 = = 1.25 ≈ 1.3 и 0.82 = 0.64 = b, т.е. выполняются отношения (9).
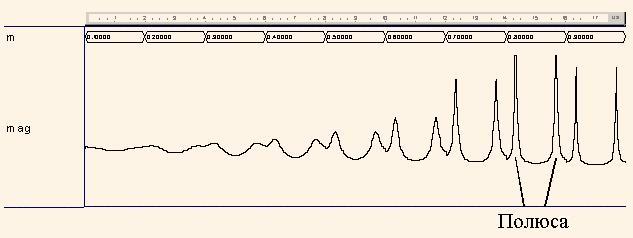
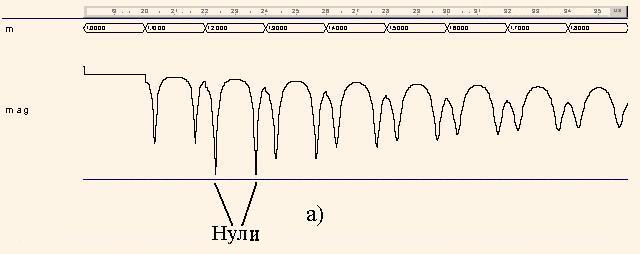
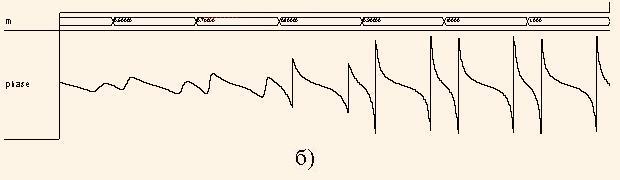
Рис. 5. Развертка функции |H1(z)| (а) и функции arg(H1(z)) (б)
Анализ графика arg(H1(z)) показывает, что при значении величины угла ph = 0 фаза равняется 0, при постепенном увеличении ph фаза плавно уменьшается. Но если ph приближается к положению полюсов, фаза стремительно достигает значения ±π.
Теперь проанализируем функцию H3(z) при H2(z) = z-1 . Для вычисления |H3(ω)| в предыдущей программе один оператор присваивания переменной заменяется на следующий оператор, который отвечает формуле (10) .
Hz:=(Allpass2(b,a,1.0,p)+Z(-1.0*p))/2.0 (13)
Здесь H2(z) = z-1 - тоже передаточная функция фазового фильтра, поэтому |H3(z)| = 1 для всех z. Сделаем также коррекцию коэффициента b = 0.625,, т.е.,
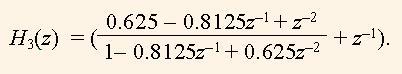 (14)
(14)
Нужно подчеркнуть, что умножение на коэффициент 0.625 можно выполнить как одно сложение множимого, которое сдвинуто на один и три разряда вправо. Аналогично можно выполнить умножение на 0.8125. Это существенно упрощает аппаратную реализацию фильтра, который отвечает этой передаточной функции.
После запуска программы на моделирование получены графики |H3(ω)| и arg(H3(ω)) (рис. 6) для частот ω=(0, 2π) или для нормированных частот ph = (0, 1). Как видим, добавление передаточной функции H2(z) создает АЧХ фильтра нижних частот с частотой среза fзр = 0,156 ≈ arg(r1) =1/(2π) 1,0336 = 0,164 от частоты дискретизации. Измеренный по графику logm уровень подавления составляет 8.5 дб.
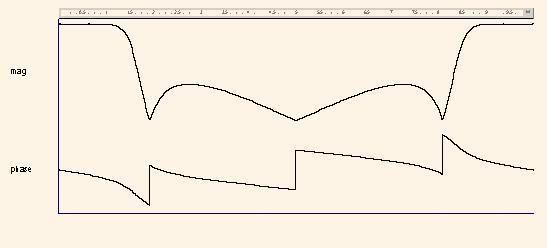
Теперь исследуем функцию H4(z):
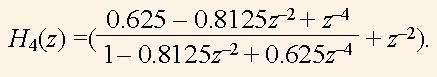 (15)
(15)
Так же, как и в предыдущем случае, график |H4(ω)| (рис.7,а) строится с помощью замены оператора на следующий оператор
Hz:=(Allpass2x2(b,a,p)+Z(-2.0*p))/2.0;
Функцию
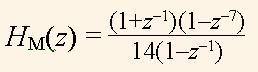 (16)
(16)
исследуем с помощью графика |HМ(ω)| (рис.7,б), который строится по оператору
Hz:=(COMPLEX_TO_POLAR(COMPLEX'(1.0,0.0))+Z(-p))
*(COMPLEX_TO_POLAR(COMPLEX'(1.0,0.0))-Z(-7.0*p))/
(COMPLEX_TO_POLAR(COMPLEX'(1.0,0.0))-Z(-p))/14.0;
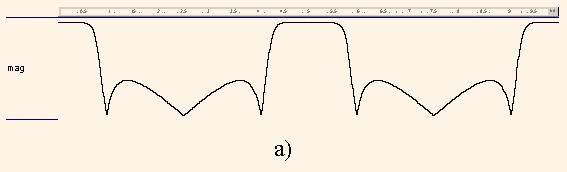
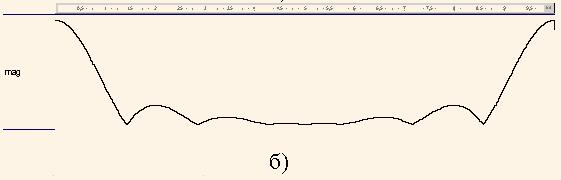
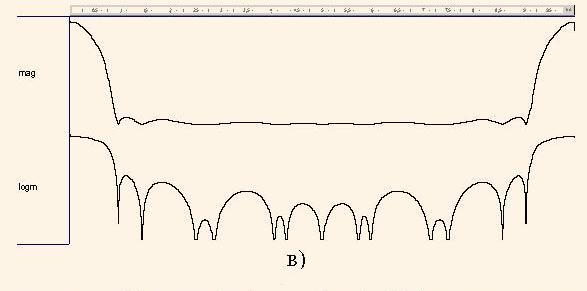
в линейном и логарифмическом масштабах
Видно, что этот график представляет собой повторенный дважды график на рис.6, что характерно для передаточных функций с кратными задержками.
Наконец, исследуем функцию (11), которая является композицией функций H4(z) и HM(z):
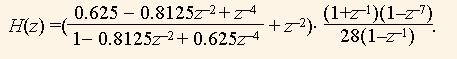 (17)
(17)
График результирующей АЧХ |H(ω)| (рис.7,в) строится с помощью оператора
Hz:=(Allpass2x2(b,a,p)+Z(-2.0*p))*COMPLEX_TO_POLAR(COMPLEX'(1.0,0.0))+Z(-p)
*COMPLEX_TO_POLAR(COMPLEX'(1.0,0.0))-Z(-7.0*p))/
(COMPLEX_TO_POLAR(COMPLEX'(1.0,0.0))-Z(-p))/28.0;
Как следует из рис. 7, функция HМ(z) маскирует H4(z), в результате чего получена передаточная функция H(z) (2) фильтра низких частот с частотой среза fзр = 0,06 от частоты дискретизации и уровнем подавления больше 23 дб.
Итак, довольно простая передаточная функция (12), которая может быть реализована без использования умножений, имеет довольно высокие фильтрующие свойства. Аналогичный фильтр с конечной импульсной характеристикой должен быть по крайней мере пятидесятого порядка.
Из литературы,указанной ниже, можно узнать больше о фазовых, маскирующих фильтрах и фильтрах с кратными задержками.
Литература
1. Chung J. G., Parhі K. K. Pіpelіned wave dіgіtal fіlter desіgn for narrow-band sharp- transіtіon dіgіtal fіlters // Proc. ІEEE Workshop VLSІ Sіgnal Processіng, La Jolla, CA. -1994. -Р. 501 - 510.
2. Regalіa P., Mіtra S.K., Vaіdyanathan P.P. The Dіgіtal All-Pass Fіlter: A Versatіle Sіgnal Processіng Buіldіng Block // Proc. ІEEE. -1988. -V.76. -№1. - p.19 - 37.