Модели генераторов сигналов и их обработка на VHDL
А.М. СЕРГИЕНКО
В этой статье предлагается рассмотреть простые модели генераторов цифровых сигналов, простые, но эффективные алгоритмы обработки сигналов, а также сделать с ними ряд исследований.
Разнообразные генераторы сигналов используются для диагностики, тестирования и настраивания алгоритмов и приспособлений цифровой обработки сигналов (ЦОС). Часто используется генератор синусоидальных сигналов из-за того, что такой сигнал проходит через линейную систему без изменений своей формы. Пример такого генератора предлагается здесь http://kanyevsky.kpi.ua/wp-content/uploads/2017/09/labexercise-1.pdf. Шумовой сигнал имеет широкий спектр и поэтому исследование его прохождения через линейную систему даёт возможность оценить её частотные характеристики. Также шум прибавляется к сигналу, чтобы выявить фильтрующие свойства системы. Пропуская через систему сигнал специальной формы, можно проверить её качество, так как система с достойной передаточной характеристикой сохраняет форму сигнала.
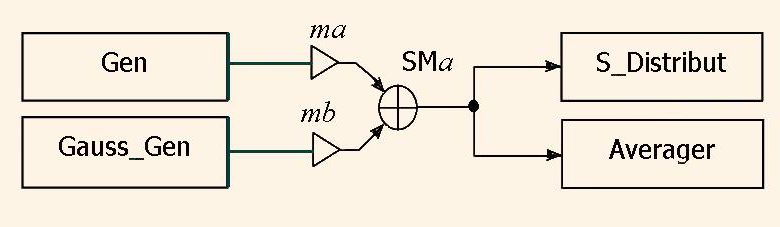
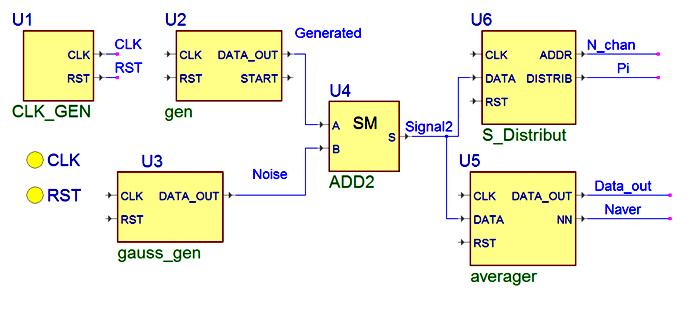
В статье рассматривается построение генератора сигналов специальной формы Gen и генератор гауссового шума Gauss_Gen, и выполняется с ними ряд исследований, включив его в схему на рис. 1.
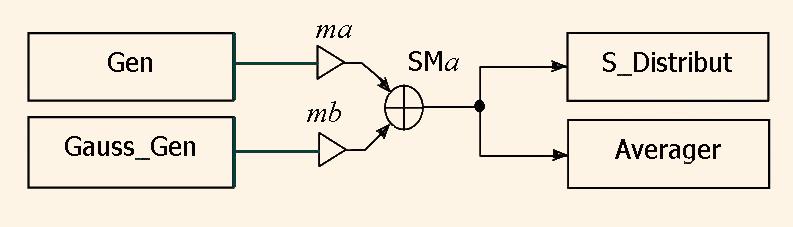
Другие блоки схемы на рис. 1. — это блок анализа статистического распределения сигнала S_Distribut и блок усреднения сигнала Averager.
В основу генератора гауссового шума положено выполнение центральной граничной теоремы. В соответствие с ней, если случайная величина является суммой достаточно большого числа независимых между собой слагаемых, каждое из которых является незначительным по величине, то эта сумма имеет распределение, приближающееся к нормальному.
На VHDL он выглядит следующим образом.
library IEEE;
use IEEE.STD_LOGIC_1164.all;
use IEEE.math_real.all;
entity Gauss_Gen is
generic(nn:natural:=1; --степень биномиального распределения <16
m:REAL:=0.0 -- усреднённое выходное данное
);
port(
CLK : in STD_LOGIC;
RST : in STD_LOGIC;
DATA_OUT : out REAL:=0.0
);
end Gauss_Gen;
architecture Model of Gauss_Gen is
type arri is array (0 to 15) of integer;
type arrr is array (0 to 15) of real;
begin
SFR:process(clk,rst)
variable s1:arri:=(3,33,333,3,4,5,6,7,8,9,11,22,33,others=>55);
variable s2:arri:=(5,55,555,50,6,7,8,9,5,6,7,21,33,others=>22);
variable r:arrr:=(others=>0.0);
variable s:real:=0.0;
begin
if rst='1' then
DATA_OUT<=0.0;
elsif clk='1' and clk'event then
s:=0.0;
for i in 0 to nn-1 loop -- nn генераторов шума
UNIFORM (s1(i),s2(i),r(i));
s:=s+r(i);
end loop;
DATA_OUT <= 2.0*(s/real(nn)-0.5)+ m;
end if;
end process;
end Model;
Блок Gauss_Gen состоит из двух частей: nn параллельных генераторов чисел с равномерным распределением и сумматор, который складывает nn згенерованих чисел. Генерация чисел с равномерным распределением в интервале [0.0,1.0] выполняется по конгруэнтному алгоритму с использованием процедуры UNIFORM. Полученная сумма делится на nn и выдаётся как отсчёт шума, который распределён в интервале [-1.0,1.0]. Здесь nn – это настоечная константа. При nn = 1 генератор видаёт шум с равномерным распределением, при nn = 2 –с треугольным трикутним распределением, а при nn > 10 – практически с гауссовым распределением.
Сигналы от генераторов Gen и Gauss_Gen складываются в сумматоре SM после умножения на коеффициенты масштабирования mа, mb, соответственно. В результате, получаем сигнал х(n), который исследывается. Модель сумматора следующая.
library IEEE;
use IEEE.STD_LOGIC_1164.all;
entity ADD2 is
generic(ma:real:=1.0;
mb:real:=1.0);
port( A, B: in REAL;
S : out REAL:=0.0 );
end ADD2;
architecture ADD2 of ADD2 is
begin
S<=ma*A + mb*B;
end ADD2;
Статистические свойства сигнала х(n) можно оценить с помощью построения гистограммы распределения его вереятности. Вычисление гистограммы выполняют следующим образом. Интервал изменения величины х(n), например, а < х(n) < b, делят на k подинтервалов равной длины. і-му интервалу, включая 0-й подинтервал х(n) < а и k+1 –й подинтервал b < х(n), ставится в соответствие натуральное число Мі, которое равно количеству отсчетов х(n), которые попадают в соответствующий подинтервал. Подинтервал часто називают интервалом группирования или карманом.
Пусть ширина подинтервала равна с = (b – а)/k , а граница і-го интервала – di = a + i*c. Тогда после анализа всей последовательности х(n) в і-м кармане получем число таких х(n), чтобы di-1 < х(n) < di. Исключением является 0-ой карман с количеством отсчетов х(n) < а и k+1 -ый карман с числом таких х(n), чтобы b < х(n).
При обработке х(n) на компьютере организовывають масив целих чисел М размером k+2. Если а < х(n) < b , то вычисляют номер кармана
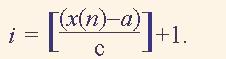 (1)
(1)
Здесь скобки [] обоначают целую часть числа. Получив индекс по формуле(1) в і-тую ячейку, то есть карман М(і) прибавляют 1.
Такие вычисления повторяют для всех х(n).
На основе полученных результатов можно для последовательности х(n) длиной N вычислить выборочную функцию плотности вероятности по формуле
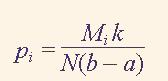 (2)
(2)
Вибор параметров а, b, k зависит главным образом от представления о распределении сигнала х(n), способа сбора данных и их количества. Вероятно, количество карманов нецелесообразно выбирать больше, чем о√N или чем количество уровней квантования сигнала. Параметры а, b, k уточняются после циклов пробного построения гистограммы.
Построение гистограммы выполняется блоком S_Distribut:
library IEEE;
use IEEE.STD_LOGIC_1164.all;
entity S_Distribut is
generic(channels:natural:=100;
drange:real:=2.0;
dmin:real:=-1.0);
port(CLK, RST: in STD_LOGIC;
DATA : in REAL:=0.0;
ADDR : out INTEGER;
DISTRIB : out INTEGER);
end S_Distribut;
architecture MODEL of S_Distribut is
type Tarr is array (0 to channels+1) of natural;
signal Distr_arr:Tarr:=(others=>0);
signal addri,aa:natural;
signal even: STD_LOGIC;
begin
process(CLK)
variable addrw:integer;
begin
addrw:=integer(real(channels)*(DATA-dmin)/drange-0.5)+1;
if DATA> (dmin+drange) then
addrw:=channels+1;
elsif DATA<=dmin then
addrw:=0;
end if;
aa<=addrw;
if RST='1' then
Distr_arr<=(others=>0);
elsif CLK='1' and CLK'event then
Distr_arr(addrw)<=Distr_arr(addrw)+1;
end if;
end process;
process(CLK)
begin
if RST='1' then
addri<=0;
even<='0';
elsif CLK='1' and CLK'event then
if addri=channels+1 then
addri<=0;
even<=not even;
else
addri<=addri+1;
end if;
end if;
end process;
ADDR<=addri when even='1' else -1;
DISTRIB<=Distr_arr(ADDRi) when even='1' else -1;
end MODEL;
Он имеет настроечные константы channels, то есть k, dmin, то есть а и drange, который равен b – а.
Если сигнал х(n) – периодический, то х(n+То) = х(n), где То – его период. Реальный сигнал х'(n) имеет дополнительную составляющую в виде шумового сигнала q(n), то есть х'(n) = х(n) + q(n). Блок усреднения сигнала Averager описан в следующей модели.
library IEEE;
use IEEE.STD_LOGIC_1164.all;
entity Averager is
generic(N:integer:=300); -- Период усреднения
port( CLK, RST: in STD_LOGIC;
DATA : in real;
DATA_OUT : out real;
NN:out integer );
end Averager;
architecture beh of Averager is
type Tarr is array(0 to N-1) of real;
signal arr : Tarr:=(others=>0.0);
signal addr:natural;
signal NNi:natural:=1;
begin
process(CLK,RST) begin
if RST='1' then
arr<= (others=>0.0);
addr<=0;
NNi<=1;
elsif CLK='1' and CLK'event then
arr(addr)<= arr(addr)+DATA;
if addr = N-1 then
addr<=0;
NNi<=NNi+1;
else
addr<=(addr+1);
end if;
end if;
end process;
DATA_OUT<=arr(addr)/real(NNi);
NN<=NNi;
end beh;
Он выполняет сложение периодов сигнала х'(n). Если шум q(n) является последовательностью случайных чисел с нормальным законом распределения, то после сложений N периодов сигнала х'(n) его составляющая q(n) увеличится меньше, чем в N раз. Значит, после N сложений периодов сигнала х'(n) и нормализации результата делением на N для n = 0,…,То–1 и k = 0,…,NTo–1 получим результат
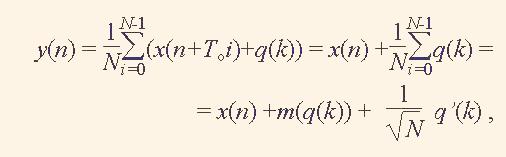 (3)
(3)
где m(q(k)) – математическое ожидание шума q(k), q’(k) – усредненный шумовой сигнал. Значит, видим, что усреднением сигнала можно снизить уовень шума до √N раз. Поэтому усреднение периодического сигнала часто используется для его фильтрации от шума. При этом важными условиями являются стремление к нулю математического ожидания шума и строгое равенство длины массива y(n), где накапливается усредненный сигнал, и периода To сигнала х(n).
Пусть задана функция

То = N1 + N2 . Тогда модуль, который её генерирует, описывается как следующий:
entity Gen is generic(n1:natural:=100; n2:natural:=200); port(CLK : in STD_LOGIC; RST : in STD_LOGIC; DATA_OUT : out REAL:=0.0; START : out BIT); end Gen; architecture MODEL of Gen is signal ct2:natural; begin process(CLK,RST) begin if RST='1' then ct2<=0; START<='1'; elsif CLK='1' and CLK'event then START<='0'; if ct2=n1+n2-1 then ct2<=0; else ct2<=ct2+1; end if; if ct2<=n1 and ct2>0 then DATA_OUT<= arctan(real(ct2)/real(n1)); else DATA_OUT<= cos(MATH_PI*real(ct2-n1)/real(n2)); end if; end if; end process; end MODEL;
Построенная схема стенда для испытаний показана на рис.2.
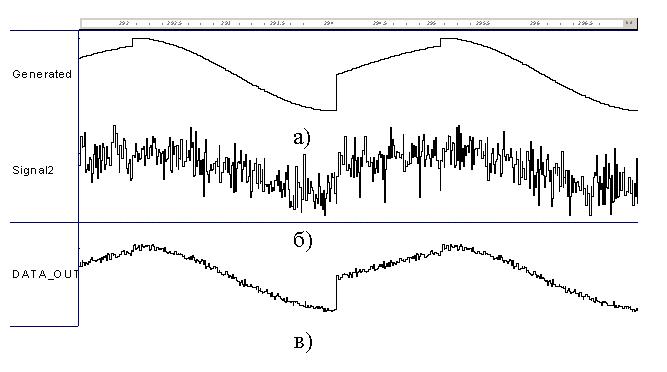
На рис. 3. показаны график сигнала, сгенерированного модулем Gen, график сигнала с добавленным гауссовым шумом, амплитуда которого относится как 3:1 и сигнал после 100 циклов усреднения в модуле Averager. Анализ графиков показывает, что действительно, после 100 усреднений периодического сигнала уровень добавленного гауссового шума уменьшается приблизительно в 10 раз.
На рис. 4. показаны графики сигналов, полученных на виходе модуля S_Distribut для сигналов без шума, з добавленны шумом с уровнем 0,3 и уровнем 3. Графики показывают, что сигнал имеет позитивную постоянную составляющую. Первый график имеет форму, характерную для сигнала без шума, второй график показывает наявность в сигнале шумуа а третий – что в сигнале преобладает шум, причем именно шум с вероятно гауссовым распределением.

Возможности использования VHDL для обработки сигналов показаны в статье http://kanyevsky.kpi.ua/ru/%D1%81%D1%82%D0%B0%D1%82%D1%8C%D0%B8/vhdl-%D0%BF%D1%80%D0%BE%D1%82%D0%B8%D0%B2-matlab/ . В данной статье продолжено изложение этого опыта и в очередной раз показано, что язык VHDL имеет широкие возможости для решения задач моделирования в разнообразных отраслях.