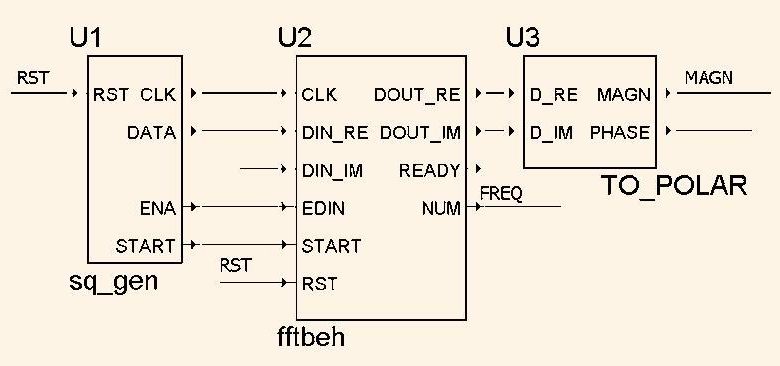
Поведінкова модель процесора ШПФ.
(З журналу ARGC & ARGV)
А. М. СЕРГІЄНКО
Щоб оцінити можливості VHDL при дослідженні алгоритмів цифрової обробки сигналів і почати на практиці їхнє використання, розглянемо розробку й застосування блоку для обчислення ШПФ.
Процедура ШПФ широко використовується в цифровій обробці сигналів для одержання амплітудного й фазового спектрів сигналу, а також для згортки довгих послідовностей відліків сигналів. В Matlab’і вбудована процедура FFT, що обчислює ШПФ для масиву N комплексних даних з плаваючою комою. Якщо N дорівнює степеню двійки, то ця процедура виконується досить швидко. Результати ШПФ можна одержати у вигляді графіків, виконавши процедуру PLOT.
У симуляторах VHDL зазвичай цифрові сигнали надходять, виробляються й спостерігаються у вигляді графіків, які одержуємо у процесі моделювання алгоритму. Але алгоритм ШПФ припускає, що дані надходять і видаються відразу у вигляді масивів. Також багато інших алгоритмів обробки, як, наприклад, вирішення систем рівнянь, вимагають аналогічного надходження даних. Тому доцільно обчислювати ШПФ як ланцюжок процедур. Перша з них, що називається Gather_C, накопичує вхідний масив комплексних початкових даних. Друга процедура – FFT – виконує алгоритм ШПФ, а заключна процедура Scatter_C видає результуючий масив у вигляді послідовності даних.
Зазначені процедури виконуються об’єктом FFTbeh. Цей об’єкт можна вставляти в потрібне місце проекту, що розробляється, як компонент, з метою виміряти спектр сигналів, які цікавлять, або відобразити сигнал з часової області в частотну. Інтерфейс цього об’єкта й перелік використовуваних стандартних бібліотек виглядає так:
library IEEE;
use IEEE.std_logic_1164.all;
use IEEE.std_logic_ARITH.all;
use IEEE.MATH_REAL.all;
use IEEE.MATH_COMPLEX.all;
entity FFTbeh is
generic(
N:positive:=8; -- 2**N -довжина перетворення
IDCT:natural:=0; -- 0- пряме, 1- зворотнє перетворення
PT:natural -- масштаб результату =2**PT
);
port (
CLK: in STD_LOGIC; -- синхросерія
RST: in STD_LOGIC; -- асинхронне скидання
START: in STD_LOGIC; -- початок накопичення вхідного масиву
EDIN: in STD_LOGIC; -- строб даних
DIN_RE: in integer; -- реальна частина даних
DIN_IM: in integer; -- уявна частина даних
DOUT_RE: out integer:=0;-- реальна частина спектра
DOUT_IM: out integer:=0;-- уявна частина спектра
NUM: out integer:=0; -- номер вихідного відліку
READY: out STD_LOGIC -- початок виводу результатів
);
end FFTbeh;
У бібліотеках ІEEE.MATH_REAL і ІEEE.MATH_COMPLEX зберігаються оголошення типу комплексного даного, такі функції, як синус, косинус, квадратний корінь, функції від комплексних аргументів та інші, які застосовуються для обчислення ШПФ.
Налагоджувальна змінна N задає довжину перетворення. При ІDCT = 0 виконується пряме перетворення, а при 1 – зворотнє. Змінна PT задає масштаб результату. Таким чином, перетворення дорівнює
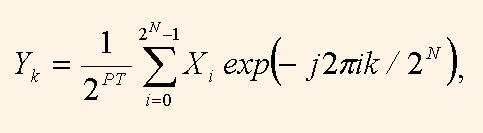
де Xі – відлік вхідних комплексних даних: DІN_RE +j*DІN_ІM, Yk – відлік комплексного спектра: DOUT_RE +j*DOUT_ІM.
По сигналу, що приходить у порт START, починається накопичення масиву вхідних даних. Закінчення обчислень ШПФ вказується сигналом з вихідного порту READY.
Відліки спектра, які видаються, супроводжуються номером відліку NUM, за яким зручно знаходити значення частоти тієї або іншої спектральної лінії.
Різні блоки обробки сигналів доцільно виконати з інтерфейсом, аналогічним інтерфейсу об’єкта FFTbeh. Тоді їх можна з’єднувати між собою послідовно, відповідно до основного алгоритму. При цьому вихідний порт READY одного блоку з’єднується із вхідним портом START наступного блоку.
Сигнал на порту EDІ стробує прийом вхідних даних. У загальному випадку, цей сигнал дозволяє роботу блоку в окремих тактах. Це необхідно для моделювання й стикування блоків, що працюють із взаємно кратними періодами дискретизації. Наприклад, за допомогою блоку FFTbeh можна визначати вузькосмуговий спектр після попередньої фільтрації смуговим фільтром і зниження частоти дискретизації в М разів. При цьому сигнал EDІ повинен мати відношення ширини імпульсу до його періоду 1:М.
Поведінка об’єкта FFTbeh описано в архітектурі FFT_іnt. Для подання масивів даних у ній оголошені наступні типи масивів комплексних і дійсних даних.
constant NN: integer:=2**N; -- довжина перетворення type MEMOC is array (0 to NN) of complex; --комплексний масив type MEMOC_2 is array (0 to NN/2-1 ) of complex; type MEMOR is array (0 to NN-1) of real; --дійсний масив
У наступному тексті описано процедуру, за якою накопичується масив вхідних комплексних даних.
procedure GATHER_C(signal CLK,START,EDIN:in std_logic;
signal DR,DI: in integer; --реальна й уявна частина відліків вхідних даних
signal rdy: out std_logic; --сигнал готовності
signal datact: inout natural;--номер даного
signal RAM:out MEMOC) -- робочий масив
is
variable TR,TI:real;
begin
wait until CLK= '1'; -- запуск процедури по фронту CLK
if EDIN = '1' then -- перевірка дозволу прийому
TR:= real(DR); -- формування комплексного даного
TI:= real(DI);
RAM(datact)<=(TR,TI); -- та запис його в масив
if datact < RAM'right then
datact<=datact+1; -- лічильник даних
end if;
if START='1' then
datact<=RAM'left; --обнулення лічильника даних
end if;
rdy<='0';
if datact =RAM'right-1 then
rdy<='1'; --масив готовий
end if;
end if;
end procedure;
Така процедура істотно відрізняється від процедур, до яких звикла більшість програмістів. В інтерфейсі процедури явно вказуються не тільки тип даних, але й те, що вони - сигнали, а також їхній напрямок: вхідні або вихідні дані. Під час виклику процедури їй не просто передається керування, а її копія переписується в модуль, що викликає процедуру, й там вона зв'язується. Виконання цієї процедури запускається за фронтом синхросигнала CLK в операторі waіt і зупиняється після виконання її останнього оператора.
У даній процедурі при кожному її запуску при EDІN = '1' у масив RAM по лічильнику datact записується чергова пара даних.
Процедура SCATTER_C виглядає так
procedure SCATTER_C(signal CLK,START,EDIN:in std_logic;
pt:natural; -- масштаб результату
signal RAM:in MEMOC; -- вхідний масив
signal datact: inout natural; -- лічильник даних
signal rdy: out std_logic; -- кінець виводу масиву
signal DR,DI: out integer ) -- вихідні дані
is
variable s:real:=real(2**pt); -- масштабний коефіцієнт
begin
wait until CLK='1';
if START='1' then
datact<=RAM'left;
elsif EDIN='1' then
RDY<='0';
DR<= integer(RAM2(datact).RE/s);
DI<= integer(RAM2(datact).IM/s);
if datact< RAM'right then
datact<=datact+1;
end if;
if datact=RAM'right-1 then
RDY<='1';
end if;
end if;
end procedure;
Ця процедура працює так само, як і попередня. Але навпаки, накопичені в масиві дані послідовно видаються на її вихід (gather - збирати, scatter - розкидати).
Нарешті, процедура, що обчислює ШПФ масиву даних виглядає так:
procedure FFT(N:positive; -- розмір перетворення =2**N
signal rdy:in std_logic; -- запуск перетворення
signal RAM_I: in MEMOC; -- вхідний масив даних
signal RAM_O:out MEMOC) -- вихідний масив спектрів
is
constant NN:positive:=2**N;
variable TWIDDLE:MEMOC_2; -- масив обертаючих коефіцієнтів
variable RAM:MEMOC; -- робочий масив
variable a,b,c,d,w: complex;
variable al:real;
variable base,itera,datact,twiddlect,twiddleinc: natural;
variable delta:integer:=1;
variable addrf: std_LOGIC_VECTOR(N-1 downto 0);
variable addri: std_LOGIC_VECTOR(N-1 downto 0);
begin
-- формування таблиці обертаючих коефіцієнтів
for i in 0 to NN/2-1 loop
al:= (MATH_PI*real(2*i))/real(NN);
if IDCT=0 then
TWIDDLE(i):=(COS(al),-SIN(al)); -- для прямого ШПФ
else
TWIDDLE(i):=(COS(al), SIN(al)); -- для оберненого ШПФ
end if;
end loop;
loop -- основний цикл
wait until RDY='1'; -- початок ШПФ
-- двійково-інверсна перестановка вхідних даних
addrf:=(others=>'0'); -- вектор адреси для прямого порядку
datact:=0;
for i in 1 to NN loop
for ind in 0 to N-1 loop -- інвертування порядку біт
addri(ind):=addrf(N-1-ind); -- інверсна адреса
end loop;
RAM(CONV_INTEGER(unsigned(addri))):=RAM_I(CONV_INTEGER(unsigned(addrf)));
addrf:=unsigned(addrf)+1;
end loop;
-- власне ШПФ
itera:=0;
delta:=1;
twiddleinc:=0;
for itera in 1 to N loop --початок ітерації
base:=0;
twiddlect:=0;
for butterfly in 0 to NN/2 - 1 loop
a:=RAM(base); -- початок базової операції
base:=base+delta;
b:=RAM(base);
w:=TWIDDLE(twiddlect);
c:=a + b * w; -- власне метелик
d:=a - b * w;
RAM(base-delta):=c;
RAM(base):=d; -- кінець базової операції
-- модифікація параметрів базової операції
base:= base + delta;
if base >= NN then
base:=base-NN+1;
twiddlect:=twiddlect+twiddleinc;
end if;
end loop; -- кінець ітерації
-- модифікація параметрів ітерації
delta:=delta*2;
if itera=1 then
twiddleinc:=NN/4;
else
twiddleinc:=twiddleinc/2;
end if;
end loop;
RAM_O<=RAM; -- результати ШПФ
end loop;
end procedure;
Тут виконується відомий алгоритм ШПФ за основою 2 з проріджуванням за часом з заміщенням даних [5]. Процедура має дві ділянки: перша з них виконується однократно на початку моделювання, а друга - власне ШПФ - виконується періодично. При виконанні першої ділянки формується таблиця обертаючих коефіцієнтів, розмір якої дорівнює довжині перетворення, і яка потім використовується алгоритмом ШПФ.
Друга ділянка являє собою нескінченний цикл. Цикл запускається, як тільки буде готовий масив початкових даних, що підготовлюється процедурою GATHER_C. Після запуску дані переписуються із вхідного масиву в робочий масив. При цьому виконується двійкова інверсія адрес запису. Слід зазначити просту й оригінальну можливість двійкової інверсії адреси, яка надається мовою VHDL. Адреса представляється бітовим вектором і біти в ньому переставляються в інверсному порядку безпосередньо. У звичайних мовах для цього необхідно виконати складний і не завжди очевидний алгоритм.
Як і всі алгоритми БПФ, даний алгоритм являє собою гніздо циклів. У внутрішньому циклі виконуються базові операції БПФ, а зовнішній цикл утворений N ітераціями алгоритму ШПФ.
Виконавча частина архітектури містить виклики описаних вище процедур:
begin
INPUT:GATHER_C(CLK,START,EDIN,
DR=>DIN_Re,DI=>DIN_IM,
rdy=>idatardy,datact=>datact_I,RAM=>RAM1);
SPECTRUM:FFT(N,idatardy,RAM_I=>RAM1,RAM_O=>RAM2);
OUTPUT: SCATTER_C(CLK,idatardy,EDIN,PT,
RAM=>RAM2,DATACT=>datact_o,
rdy=>rdy,DR=>DOUT_RE,DI=>DOUT_IM);
DEL:process(CLK) begin
if CLK='1' and CLK'event and EDIN='1' then
READY<=idatardy;
NUM<= datact_o;
end if;
end process;
end FFT_int;
Для розуміння виконання програми варто нагадати, що паралельний виклик процедури, у якій застосовується оператор waіt, еквівалентний операторові процесу, тіло якого складається з тіла процедури. Таким чином, всі три процедури, як і еквівалентні їм процеси, виконуються паралельно в деякому конвеєрному режимі. При цьому дані й керування передаються від процедури до процедури як між ступенями конвеєра. У результаті, об'єкт FFTbeh обробляє безперервний потік даних, сегментуючи його на блоки довжиною 2**N.
Процес DEL виконує затримку сигналу готовності READY і потоку номерів NUM відліків результату на один такт, щоб вони відповідали вихідним відлікам сигналів DOUT_RE і DOUT_ІM .
Розглянемо простий приклад застосування об'єкта FFTbeh для виміру спектра сигналу, що видається генератором прямокутних імпульсів. Графічна програма, підготовлена в середовищі Aldec Actіve HDL, показана на рис.1.
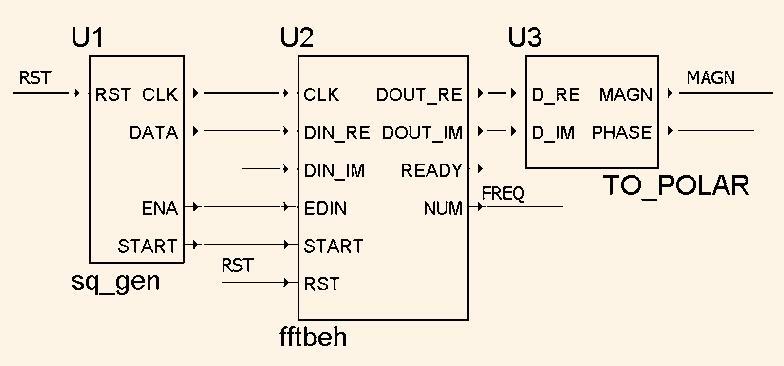
Тут компонент U1 являє собою програмований генератор прямокутних імпульсів DATA з видачею синхросерії CLK, сигналів START і ENA. Компонент U2 - це описаний вище блок ШПФ, а U3 - перетворювач комплексних чисел із прямокутної системи координат у полярну.
VHDL - симулятор може видавати на екран цілочисельний сигнал у вигляді графіка. Як правило, цей графік з осями представлений за допомогою засобів векторної графіки. Тому його можна виділити й через "кишеню" ПК перемістити, наприклад, у редактор тексту, такий як MS Word. На рис.2. показані графіки сигналів, згенерованих при моделюванні моделі на рис.1. У цьому експерименті визначався спектр прямокутного імпульсу з періодом 256 тактів і тривалістю 10 тактів за допомогою БПФ довжиною 256 відліків.
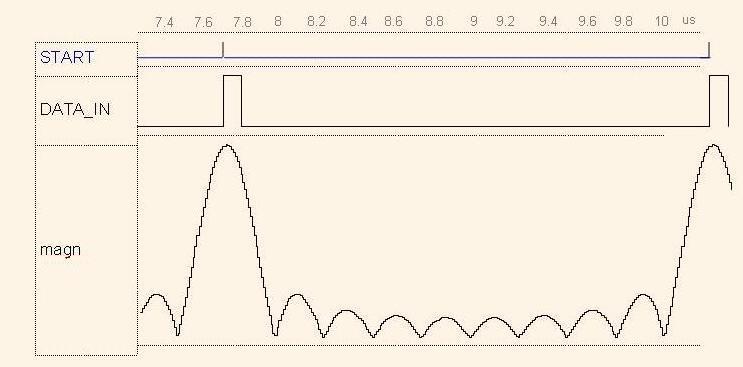
Як бачимо, запропонований блок БПФ ефективний у використанні. Одержувані за його допомогою графіки спектра зручні як для сприйняття, так і для документування й збереження. Причому швидкість виводу графіків і швидкодія системи при їхньому вивченні (переміщення, зміна масштабу, вимір у заданих точках) багаторазово вище, ніж при використанні Matlab'у.
При необхідності, описаний блок ШПФ можна легко доробити для того, щоб вхідні і вихідні дані були із плаваючою комою. Така доробка зводиться лише до заміни цілого типу даних на тип real.