Генератор модулів фільтрів для ПЛІС
Фільтри зі скінченною імпульсною характеристикою (СІХ-фільтри) широко використовуються в системах цифрової обробки сигналів через їхню високу швидкодію та лінійну фазову характеристику. Реалізація СІХ-фільтрів на програмованих логiчних iнтегральних схемах (ПЛІС) має ряд переваг. Це висока продуктивність, малі апаратні витрати, швидке перенастроювання та висока якість фільтрування завдяки повній адаптації реалізованої структури алгоритму фільтрації, сумiсна реалiзацiя з iншими блоками обробки в межах системи на кристалi.
Однією з основ сучасної технології розробки систем на кристалі є використання в проектах обчислювальних модулів з заданими параметрами, що генеруються за допомогою спеціальної програми – генератора модулів. Генератор модулів СІХ-фільтрів може спростити й прискорити розробку проектів, де необхідні СІХ-фільтри з заданими амплітудно-частотною характеристикою й розряднiстю даних. Генератор СІХ-фільтрів з пакету Xilinx FIR СoreGen™ став широко відомим завдяки високій швидкодії, невеликим апаратним витратам генерованих ним фільтрів [1]. Але цей генератор генерує модулі фільтрів, які представлені за допомогою схеми на логічному рівні з заданими вiдносними координатами логiчних елементів, через що діапазон настроюваних параметрів є невеликим і згенеровані модулі використовуються в обмеженій множині мікросхем ПЛІС.
В статті описані особливості розробки нового генератора модулів СІХ-фільтрів, що генерує фільтри, описані мовою VHDL, які мають підвищену швидкодію, мінімізовані апаратні витрати, широкий діапазон зміни параметрів довжини характеристики, розрядності даних і коефіцієнтів і які можуть бути реалізовані в будь-якій серії ПЛІС, або замовленій НВІС.
Обчислення СІХ -фільтра полягає в знаходженні наступної суми добутків:
yn = a1xn +…+ akxn-k+1+… +aKxn-K+1 ,
де xn – вхідні дані, ak – коефіцієнти імпульсної характеристики, K – довжина імпульсної характеристики, yn – вихідні результати з індексом n. На один відлік результату припадає близько K множень і додавань. Тому операція згортки є досить трудомісткою.
В бiльшостi проектiв у СІХ-фільтрах виконується множення на сталу. Тому тут застосування комбінаційних схем множення є досить збитковим. Крім того, число блоків множення в нових серіях ПЛІС, як в Xilinx VirtexІІ™, є обмеженим і часто недостатнім для вирішення багатьох задач. Відомо ряд способів, що використовують властивості блоків множення на сталу. Наприклад, вважаючи, що середнє число одиничних бітів в m – бітовій константі дорівнює m/2, розробляють блок множення на сталу, як дерево з m/2-1 суматорів, тобто в 2 рази менше, ніж у звичайного блока множення.
В роботі [2] було запропоновано метод одержання суми добутків, який називається розподілена арифметика. Метод полягає в збереженні в ПЗП 2K комбінацій сум K коефіцієнтів. Якщо i-й зріз бітів вхідного набору даних подається на адресний вхід такого ПЗП, то з нього зчитується відповідна сума часткових добутків. Результат одержується пiсля додавання m таких сум з відповідним зсувом розрядів до числа в акумуляторі результату.
Такий спосіб був запропонований в роботі [3] як спосіб одержання суми добутків в ПЛІС. При цьому 4-входова логічна таблиця (LUT) програмується як швидкісний 16-бітовий ПЗП. Цей спосіб широко використовується також і в генераторі Xilinx FIR СoreGen™ [1]. З метою одержання високої швидкодії всі суми часткових добутків для i–тих бітів коефіцієнтів обчислюються паралельно. Тому такі схеми фільтрів називають фільтрами з паралельною розподіленою арифметикою (parallel distributed arithmetic -PDA). Недоліком цього способу є великий об’єм ПЗП, якщо число коефіцієнтів K фільтра більше, ніж 8-12. Для зменшення цього недоліка структуру фільтра ділять на блоки, кожен з яких обчислює суму K=4 або 5 добутків.
В роботі [4] опубліковано інший ефективний спосіб множення в ПЛІС. Він побудований на використанні ПЗП, в i-й комірці якого зберігається коефіцієнт a, помножений на число i. Тому ПЗП з об’ємом 2m є блоком множення на сталу для m -бітових даних. Далі детально описується такий самий спосіб, але який раніше був запропонований в [5].
Коли допустимий об’єм ПЗП надто малий, то вхідні дані розділяються на l вирізок з p розрядів, так що m ≤ lp, а результат одержується як сума l часткових добутків. В [5] було показано, що такі блоки множення при реалізації в НВІС є більш ефективними, ніж звичайні блоки множення 16-розрядних даних, якщо сумарний об’єм ПЗП не більший, ніж 4 кілобайта, а оптимальний розмір вирізки розрядів дорівнює p = 4. Приклад структури такого блоку множення на сталу для 16-розрядних даних і p = 4 показано на рисунку 1.
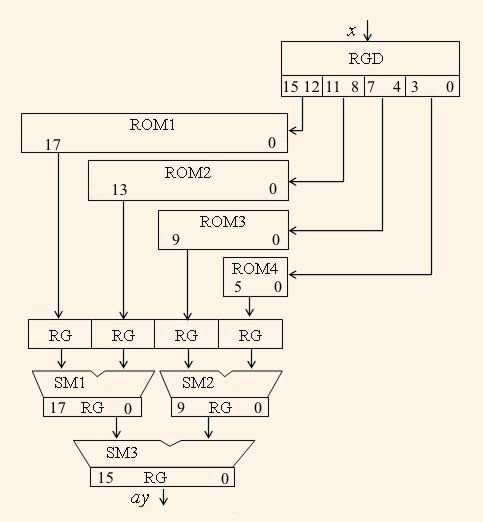
Така реалізація блоку множення на сталу в ПЛІС має наступнi переваги:
* Висока продуктивність. Схема такого блоку може бути реалізована як конвеєр з мінімізованою затримкою у всіх його ступенях. Тому мінімальний період циклу синхронізації дуже короткий і не перевищує затримки одного суматора.
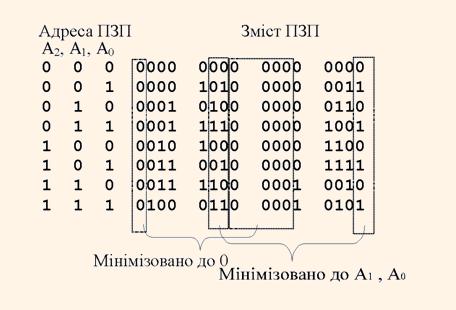
* Зменшений об’єм апаратури. Результуючий об’єм апаратури фільтрів з такими блоками множення не більший або значно менший, ніж об’єм апаратури фільтрів PDA. Це зобумовлено наступною причиною. Нехай коефіцієнт a має послідовність j однакових розрядів (одиничних або нульових). Тоді в ПЗП вирізка з j-p+1 розрядів буде зберігати біти, які дорівнюють один одному. Крім того, часто однорозрядні вирізки повторюють стан розрядів адреси. При трансляції в логічну схему компілятор-синтезатор на стадії мінімізації апаратних витрат замінює вирізку такого типу з цього ПЗП на генератор константи й підключає деякі вихідні розряди до розрядів адреси. Цей ефект проілюстровано на рисунку 2 для випадку множення на коефіцієнт 0,62573 при р=3.
СІХ-фільтри, які зазвичай використовуються на практиці, мають більше, ніж 70% коефіцієнтів, які мають більше j = 4 однакових старших розрядів і близько 40% коефіцієнтів що мають більше, ніж 7 таких розрядів. Тому, за рахунок мінімізації кодування тільки цих розрядів в ПЗП, результуючий фільтр матиме в 1.1,…,1.6 разів менше апаратних витрат, ніж фільтр типу PDA, в залежності від набору коефіцієнтів фільтра.
* Збільшена еквівалентна розрядність коефіцієнтів. Така властивість пов’язана з тим, що якщо коди коефіцієнтів запам’ятовувати в ПЗП і округляти до m розрядів не перед множенням коефіцієнта a на константу i, а після такого множення, то до молодших розрядів кратних множників додаються кратні відкинуті розряди. Тому еквівалентна розрядність коефіцієнтів у фільтрах може бути оцінена як m-2, де m дорівнює максимальній розрядності ПЗП, який використовується в даному фільтрі. При тих же умовах розрядність коефіцієнтів у фільтрі типу PDA дорівнює лише m-p.
Авторами розроблено генератор модулів СІХ-фільтрів, які використовують блоки з множенням на основі ПЗП. Генеровані фільтри мають звичайну структуру, яка включає блок внутрішніх регістрів для конвеєрної затримки вхідних даних і дерево суматорів, яке обчислює суму затриманих і зважених даних. Для підтримки високої продуктивності схема фільтра глибоко конвеєризована.
Модулі, що генеруються, описані одним VHDL–файлом. Такий файл може бути скомпільованим будь-якою синтезуючою програмою в файл схеми на логічному рівні для будь-яких ПЛІС фiрм Xilinx, Altera та інших. Завдяки тому, що в проектi фiльтра немає обмежень на розмiщення логiчних елементів, уможливлюється максимальне використання ресурсiв ПЛІС.
Генератор СІХ-фільтрів розроблено з використанням програми Win32 Delphi з вікном настройки. Також генератор виконано з керуванням командним рядком i задаванням параметрiв фiльтра в окремому файлi. Користувачі можуть змінювати наступні параметри фільтрів:
- набір коефіцієнтів, які можуть задаватись як десяткові, восьмиричні, шіснадцятиричні, двійкові цілі числа або числа в форматі з плаваючою комою;
- розрядність вхідних і вихідних даних від 4 до 24 біт;
- розрядність коефіцієнтів від 4 до 24 біт;
- число коефіцієнтів від 4 до 128;
- фільтри з симетричною, несиметричною або антисиметричною імпульсною характеристиками;
- вхідні дані додатні або знакові;
При іспитах генератора було згенеровано набір СІХ-фільтрів, які були сконфігуровані в ПЛІС фірми Xilinx за допомогою САПР Xilinx Foundation 3.1. Для цього були використані набори коефіцієнтів, які зустрічаються на практиці, а саме – коефіцієнти фільтрів нижніх частот і смугових фільтрів з симетричною імпульсною характеристикою з рівнем сигналу в смузі затримання –60,…,-70 дб. Деякі результати для 16 – розрядних даних і коефіцієнтів дані в наступній таблиці. Апаратні витрати приведені в числі еквівалентних конфiгурованих логiчних блокiв (ЕКЛБ). Результати для фільтрів, згенерованих за допомогою програми Xilinx FIR PDA СoreGen, показані для порівняння в нижньому рядку таблиці.
Таблиця 1.
Порiвняльнi характеристики згенерованих фiльтрiв
| Мікросхема | Число кое-фіцієнтів, K | Апаратні витрати, ЕКЛБ | Максимальна частота дискретизації, MГц |
| VirtexE-8 | 20 | 1022 | 212 |
| VirtexE-8 | 99 | 5151 | 208 |
| XC4000XV-07 | 20 | 1008 | 76 |
| XC4000XV-07 | 20 | 1457 | 50 |
Аналіз таблиці показує, що результуючі структури фільтрів мають високу продуктивність і мінімізовані апаратні витріти. Апаратні витрати практично пропорційні кількості коефіцієнтів, а максимальна частота дискретизації майже не залежить від кількості коефіцієнтів i наближається до межi, що забезпечує ПЛIС даної серiї.
Розроблений новий генератор моделей СІХ-фільтрів, що синтезуються, використовує функціональні властивості ПЛІС і мінімізує апаратні витрати результуючого проекту. Він забезпечує розробку сильно конвеєризованих структур з високими тактовими частотами, які можуть досягати значення більше, ніж 200 MГц для сучасних ПЛІС. Заготовки, що генеруються, описані на мові VHDL і представлені одним файлом і таким чином, що можуть бути скомпільовані у будь-яку серію ПЛІС або замовлену НВІС.
1. Parallel Distributed Arithmetic FIR filter. Product Specification. Available at http://www.xilinx.com. Feb. 8. 1988.
2. Peled A., Liu B. A New Hardware Realization of Digital Filters. IEEE Trans. on Acoustic Signal, Speech Processing, V.ASSP-22, June, 1974.
3. Mintzer L. FIR filters with the Xilinx FPGA. FPGA’92, ACM/SIGDA Workshop on FPGAs, 1992, pp. 129-134.
4. Chapman K. Constant Coefficient Multipliers for the XC4000E. Application Note. Available at http://www.xilinx.com. December 11, 1996.
5. Kаневский Ю.С., Некрасов Б.A., Сергиєнко A.M. К вопросу о разработке высокопроизводительних процессоров БПФ. УCиM,-1986.-№4,-с. 60-63.