Алгоритм і структура модуля для обчислення квадратного кореня у ПЛІС

SQRT_pdfDownload

УДК 004.383

Анатолій Сергієнко, Хасан Мухамед Джамал, Павло Сергієнко

Anatoliy Sergiyenko, Hasan Muhammad Jamal, Pavlo Serhienko.  Algorithm and structure of the square root calculator implemented in FPGA.

Розглядається розробка апаратних пристроїв для обчислення функції квадратного кореня за ітераційним алгоритмом. Запропонований алгоритм дає змогу прискорити обчислення функції квадратного кореня та зменшити апаратні витрати за рахунок обчислення кількох ітерацій табличним методом. Запропонований алгоритм розрахований на реалізацію у програмованих логічних інтегральних схемах.
Ключові слова: ПЛІС, квадратний корінь, конвеєр.

The development of the hardware units for the square root (SQRT) function calculations is considered, which is based on the CORDIC-like iterative algorithm. The proposed algorithm helps both to speed-up the SQRT function calculations and to minimize the hardware volume due to substituting some iterations by the look-up tables. The algorithm is intended for the SQRT function implementation in FPGA. Key words: FPGA, SQRT, CORDIC, pipeline.

Вступ. Функція квадратного кореня √x — важлива елементарна функція в наукових розрахунках, обробці цифрових сигналів та обробці зображень [1]. Наприклад, вона використовується у нейронних мережах [2]. В даний час багато задач вирішуються у програмованих логічних інтегральних схемах (ПЛІС), де також необхідно розраховувати функцію √x.

Існують різні віртуальні модулі для обчислення функції √x, які пропонуються виробниками ПЛІС та сторонніми компаніями [3]. Але ці модулі були розроблені десятиліття тому, і вони, як правило, не враховують особливості нових поколінь ПЛІС. Тому такі модулі потребують модернізації. У роботі [4] запропоновано вдосконалений алгоритм обчислення функції √x, який орієнтований на реалізацію у ПЛІС. У даній роботі пропонується ще один алгоритм, який ефективно реалізується у ПЛІС.

Алгоритми “цифра за цифрою”. Виконання алгоритму розрахунку елементарної функції типу “цифра за цифрою” зводиться до повторення одноманітних ітерацій, результатами яких є чергові точні цифри результату. Відомий алгоритм CORDIC, який призначений для розрахунків √x, полягає в наступному. Він обчислює функцію atanh(x/y). Але побічним результатом є функція K √x2+y2, а за рахунок заміни x = A + 0.25, y = A – 0.25, отримують K √A[3,5]. Недоліками цього алгоритму є додаткове множення результату на коефіцієнт 1/K ≈ 1.207 і повторення деяких ітерацій для збіжності алгоритму.

Більш конструктивним алгоритмом є алгоритм “цифра за цифрою” обчислення функції √x[4], який базується на наступних співвідношеннях. Для кожного числа x ∈[0.25; 1.0] знаходять коефіцієнти ai ∈ [0; 1], такі що

Звідси

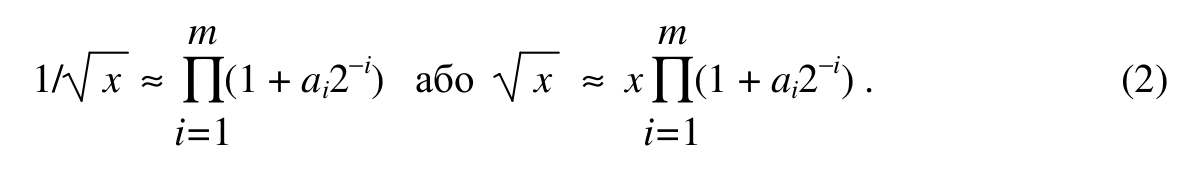
Отже, обчислення функції √x  полягає у виконанні конвергентного процесу, згідно з яким вираз (1) наближається до одиниці, в той час як вираз (2) наближається до шуканого значення. Алгоритм цього процесу виражається наступним чином:

x[0]= x;y[0]= x;
for(i = 0, i < n, i++) {
	t = x[i] + 2^(-i)*x[i];
	q = t + 2^(-i)*t;
	if (q < 1) {
		x[i+1] = q;
		y[i+1] = y[i] + 2^(-i)*y[i];}// a[i]=1
	else {
		x[i+1] = x[i];
		y[i+1] = y[i];}// a[i]=0
}
Результатом є y[n] = √x .

Модернізований алгоритм. Найбільшу затримку розглянутого алгоритму дає подвійне додавання зсунутих даних з результатами t та q. Ці обчислення можуть бути замінені одним етапом:

q = xi + 2–m xi + 2–m (xi + 2–m xi) = xi + 2–m+1xi + 2–2m xi

Оскільки у сучасних ПЛІС трьохвходовий суматор реалізується як один ступінь, який будується на основі шестивходових логічних таблиць (ЛТ), то такі обчислення можуть бути виконані за один такт без додаткових затримок і витрат на обладнання. Аналіз алгоритму показує, що коли i досягає межі n/2, то старші розряди числа xiстають одиничними а iстарших розрядів yіє точними старшими розрядами результату. Отже, решту отриманих бітів можна обчислити після аналізу та розрахунку різниці 1 – xi.

Нехай   ε1 = 1 – xn/2,    εx = √x– yn/2.   Ці величини згідно з (1) і (2) дорівнюють

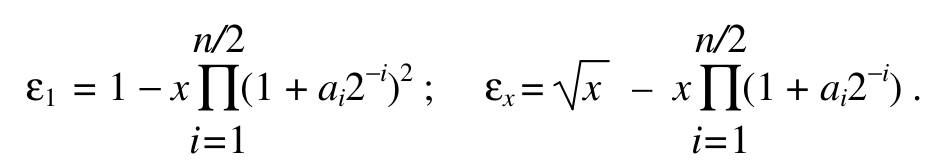
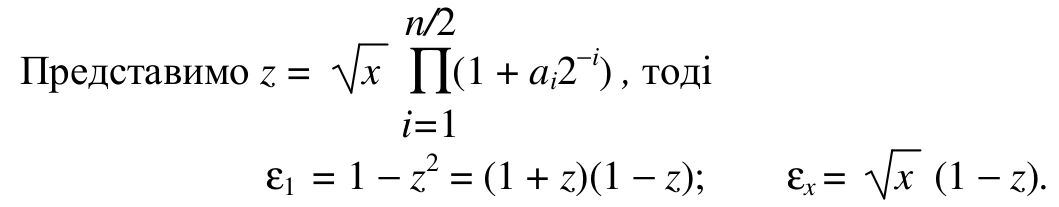
, тоді

ε1 = 1 – z2 = (1 + z)(1 – z);                εx= √x(1 – z).

Оскільки z ≈ 1, то ε1 ≈ 2(1 – z);    і   εx ≈√x      ε1 / 2 ≈ yn/2(1 – xn/2) / 2. Тоді результат дорівнює yn = yn/2 + yn/2(1 – xn/2) / 2 та модернізований алгоритм є наступний:

x[0] = x; y[0] = x;
for (i = 0; i < n/2; i++){
	q = xi + 2-i+1 * xi + 2-2i * xi;
	if (q < 1.0){
		xi+1 = u;
		yi+1 = yi + 2-i-1 * yi;}
	else {
		xi+1 = xi ;
		yi+1 = yi ;}
}
y = yi+1 + yi+1 * (1.0 - xi+1) / 2;

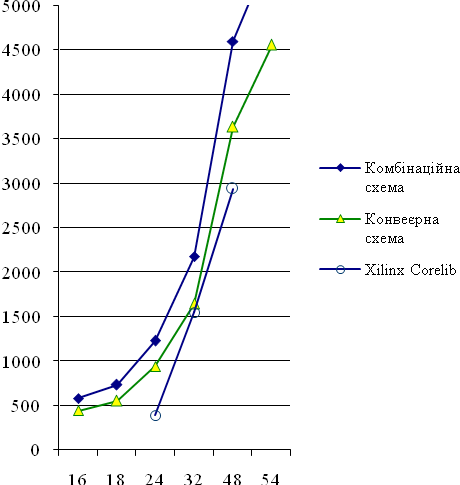
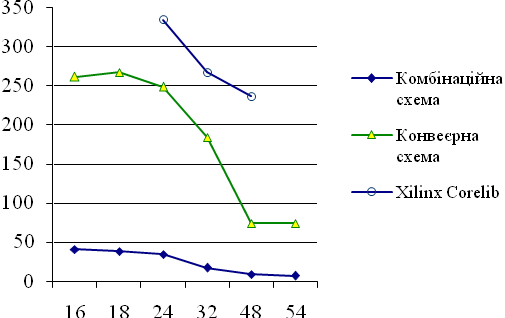
Експериментальні результати. Отриманий алгоритм був описаний мовою VHDL як віртуальний модуль. Цей модуль було зконфігуровано для ПЛІС Xilinx Spartan-6 для різної розрядності вхідних і вихідних даних. На рисунках 1 та 2 наведено залежність апаратних витрат в кількості ЛТ, а також максимальної тактовової частоти від розрядності nвхідних даних і результатів для комбінаційної і конвеєрної схем цього модуля, відповідно. Слід відзначити, що модулі з розрядністю 32 додатково мають один блок множення DSP48, а решта — чотири таких блоки.

Для порівняння, на рис. 1, 2 показані характеристики віртуальних модулів, які пропонуються компанією Xilinx Inc. Загалом, запропонований модуль має більші апаратні витрати і меншу тактову частоту. Це пояснюється тим, що модуль, який генерується засобом Xilinx Coregen, описаний на рівні ЛТ і тригерів і тому адаптований до архітектури ПЛІС конкретного типу. А запропонований модуль, хоча і не потребує тривалого генерування, повинен бути зкомпільованим синтезатором, який виконує ефективну, але не оптимальну оптимізацію.

Переваги запропонованого модуля полягають в тому, що він є безкоштов­ним і може бути налаштований на довільну розрядність вхідних та вихідних даних, а також для будь-якого типу ПЛІС. Крім того, запропонований модуль має нижчу латентну затримку, що є важливим, наприклад, при виконанні на його основі операцій з плаваючою комою. Наприклад, для розрядності 24 біт, латентна затримка становить лише 15 тактів проти 25 тактів у конкурентного ядра. Це означає, що при виконанні розрахунків з плаваючою комою запропонований модуль забезпечує більшу продуктивність.

Рис.1. Апаратні витрати блоку √x , ЛТ, в залежності від n
Рис.2. Максимальна тактова частота, МГц, блоку √x  в залежності від n

Висновки. Запропоновано модифікований алгоритм “цифра за цифрою” для обчислення функції квадратної кореня. Алгоритм відрізняється мінімізованою√x кількістю ітерацій, яка приблизно удвічі менша за кількість розрядів результату. Алгоритм описаний мовою VHDL і призначений для реалізації у ПЛІС будь-якої серії. Найбільш ефективна його реалізація при обчисленні функції √x  з плаваючою комою.

Список використаних джерел

  1. Woods R. FPGA-based Implementation of Signal Processing Systems / J. McAllister, G. Lightbody, Y. Yi / J. Wiley and Sons, Ltd., Pub. 2008. 364 p.
  2. FPGA Implementations of Neural Networks”. A. R. Omondi, and J. C. Rajapakse, Eds. Springer. 2006. 360 p.
  3. Yoshikawaa K. Development of Fixed-point Square Root Operation for High-level Synthesis / N. Iwanagaa, A. Yamawaki // Proc. 2nd Int. Conf. on Industrial Application Engineering. 2014. P. 16 — 20.
  4. Сергієнко А. М. Реалізація функції квадратного кореня у ПЛІС / П. А. Сергієнко // Вісник НТУУ «КПІ»: Інформатика, управ­ління та обчислю­вальна техніка: [зб. наук. пр.] Київ. 2014. Т.60, С. 40­ — 45.
  5. Бікташева С. Р. CORDIC-метод обчислення квадратного кореня / С. Р. Бікташева, Л.В. Мороз, М. Ю. Стахів // Вісн. Нац. Ун-ту “Львівська політехніка”. Сер.: Електроніка : [зб. наук. пр.] Львів : Вид-во Нац. ун-ту “Львів. політехніка”, 2006.  С. 152—155.
  6. Chen T.C. Automatic computations of exponentials, logarithms, ratios and square roots. // IBM J. Res. and Develop. 1972. №4. P. 380 — 388.
SQRT_pdfDownload