Бібліотека модулів для швидкого перетворення Фур’є
СЕРГІЄНКО А.А., СЕРГІЄНКО А.М.
БІБЛІОТЕКА МОДУЛІВ ДЛЯ ШВИДКОГО ПЕРЕТВОРЕННЯ ФУРʼЄ
Розглянуто набір модулів для r-точкового швидкого перетворення Фурʼє (ШПФ) за алгоритмом Вінограда. Модулі розроблені методом відображення просторового графу синхронних потоків даних у апаратуру, який забезпечує мінімізовані апаратні витрати за рахунок зменшення пропускної здатності у
r разів. Модулі призначені для побудови швидкісних конвеєрних процесорів ШПФ на базі ПЛІС.
A set of soft IP cores for the Winograd r-point fast Fourier transform (FFT) is considered. The cores are designed by the method of spatial SDF mapping into hardware, which provides the minimized hardware volume at the cost of slow-down of the algorithm by r times. The cores are intended for the high-speed pipelined FFT processors, which are implemented in FPGA.
Ключові слова: алгоритм Вінограда, швидке перетворення Фурʼє, ПЛІС.
1. Вступ
Конвеєрні процесори швидкого перетворення Фурʼє (ШПФ) за основою, яка не дорівнює 2 k , k = 1,2, використовуються у швидкісних модемах, для обробки радіосигналів та ін. Велика множина таких процесорів реалізується в програмованих логічних інтегральних схемах (ПЛІС). Недоліками існуючих конвеєрних процесорів ШПФ є необхідність узгодження потоків даних між їх ступенями та високі апаратні витрати [1,2].
У роботі розглядається проектування конвеєрних модулів для процесорів ШПФ за взаємно-простими основами, що конфігуруються в ПЛІС.
2. Модулі для малоточкового ШПФ
Конвеєрний процесор ШПФ зі взаємно-простими основами має менші апаратні витрати і придатний для обробки послідовностей з іншою довжиною, ніж 2 k . Причому обчислення ШПФ для коротких послідовностей ефективно виконувати за алгоритмом Вінограда [2,3]. При цьому виникає проблема узгодження потоків даних між модулями малоточкового ШПФ, оскільки група даних, яка видається одним модулем, не співпадає за числом даних та їх порядком з групою даних, яка примається іншим модулем [1]. Для узгодження двох модулів з паралельним виводом n даних та паралельним вводом m даних між ними слід встановити n ⋅ m блоків буферної памʼяті.
Найпростіше ця проблема вирішується тоді, коли за один такт блок видає чи сприймає лише одне дане. У цьому випадку період L-точкового ШПФ має дорівнювати L тактів, а не один, як у процесорів, описаних в [1,2]. Тоді для організації покрокового введення та по-перше, мати на входах і виходах відповідні буферні схеми, по-друге, виконувати обчислення лише в кожному L-му такті.
При використанні методики побудови просторового графу синхронних потоків даних (ГСПД) такі етапи синтезу конвеєрного процесора, як вибір ресурсів, складання розкладу, призначення операцій на ресурси і одержання структури виконуються за один крок, що дає змогу краще оптимізувати шукану конвеєрну структуру [4]. При цьому мінімізується як кількість суматорів, так і складність мультиплексорів на їх входах. Саме за цією методикою була розроблена бібліотека модулів для малоточкового ШПФ. Кожен модуль виконує L-точкове ШПФ за алгоритмом Вінограда з періодом L тактів.
3. Приклад синтезу модуля ШПФ
Розглянемо приклад розробки модуля для r = 3-точкового ШПФ, який виконує алгоритм Вінограда, описаний в роботі [4]:
t = x 1 + x 2 ; p = x 2 – x 1 ; m 0 = x 0 + t; m 1 = (cos(2π/3) – 1)⋅t; m 2 = j⋅sin(2π/3)⋅p; s = m 0 + m 1 ; X 0 = m 0 ; X 1 = s + m 2 ; X 2 = s – m 2 ;
де {x 0 , x 1 , x 2 }, {X 0 , X 1 , X 2 } − комплексні дані та
результати, j = √−1, причому m 1 = − 1,5⋅t.
Для мінімізації числа блоків множення та збільшення тактової частоти множення на коефіцієнт виконується через зсуви та додавання
множеного. Так,
k = sin2π/3 = 0,866025 = 1.00 ̄1 0 00 ̄1 0 0 ̄1 0 ̄1 01.
Тоді множення k ⋅ p виконується як
k ⋅ p = p − (p+ p2 −4 )2 −3 + ((p2 −2 − p)2 −2 − p)2 −10 .
Просторовий ГСПД для цього алгоритму з періодом обчислень L = 3 з урахуванням множення на коефіцієнт показано на рис.1. Тут вершина додавання показана як коло з хрестиком, невелике коло означає затримку на такт, великі крапки – вершини вводу і виводу, дуга, навантажена значенням “>>k” означає передачу операнду зі зсувом вправо на k розрядів. Координати вершини (s, t) означають номер s процесорного елементу (ПЕ), в якому виконується даний оператор і номер такту t виконання. На рис. 1 координати s є умовними – вони позначають назву ПЕ, в який відображається віповідна операторна вершина.
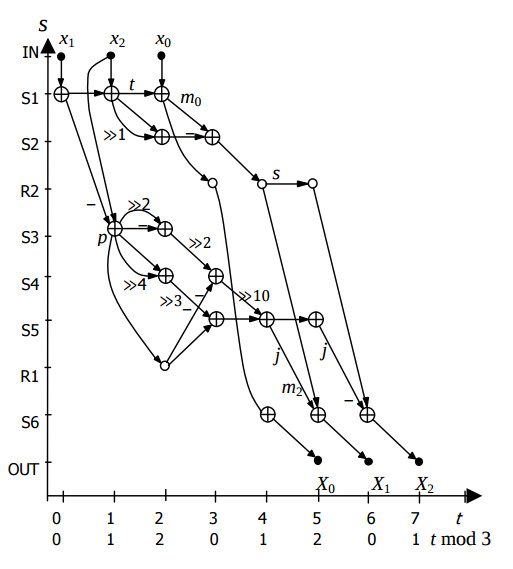
ШПФ
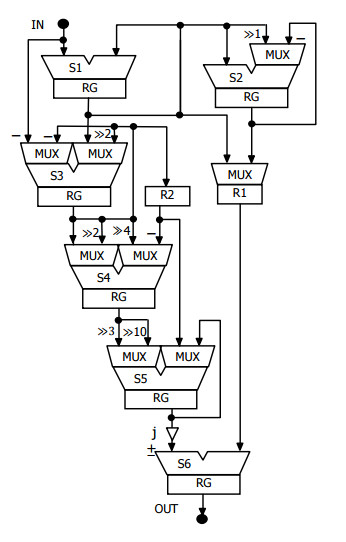
ГСПД на рис.1. відображається в структуру модуля, яку показано на рис.2. Насправді, структури модулів ШПФ не будуються. Замість цього, просторовий ГСПД описується мовою VHDL за методикою, представленою у роботі [4]. Тоді такий опис приєднується до проекту процесора ШПФ і компілюється
загальновживаним компілятором-синтезатором для ПЛІС.
4. Результати реалізації модулів
Модулі малоточкового ШПФ описані мовою VHDL і мають мінімальну кількість регістрів та суматорів. Причому вхідні та вихідні дані слідують у потрібному порядку.
У таблиці показані результати синтезу модулів для ПЛІС серії Xilinx Kintex-7 для 16-розрядних вхідних даних. Аналіз таблиці показує, що використання спеціалізованих блоків множення на константу дає змогу збільшити тактову частоту до 1,6 разів у порівнянні зі структурою з застосуванням інтегрованих блоків множення DSP48. Тактова частота модулів дорівнює частоті дискретизації сигналу. Вона є доволі високою і зменшується зі збільшенням складності модуля. Це роз’яснюється тим, що через складність розміщення та трасування на затримку у лініях зв’язку припадає 70-80% від загальної затримки у критичному шляху.
Розроблені модулі ШПФ, які описані мовою VHDL, зібрані у бібліотеку. Додатково інтерфейс кожного модуля описано мовою XML у форматі стандарту IP-XACT.
Результати конфігурування модулів у ПЛІС
| Кількість точок | Апаратні витрати, ЛТ + DSP48 | Тактова частота, МГц |
| 3 | 245 | 640 |
| 3 | 201 + 2 | 433 |
| 4 | 215 | 548 |
| 5 | 945 | 435 |
| 8 | 1187 | 424 |
| 15 = 3⋅5 | 2131 | 346 |
| 16 | 3616 | 368 |
| 64 = 8⋅8 | 1985 + 4 | 338 |
| 128 = 8⋅16 | 5277 + 4 | 324 |
Такий опис вміщує метадані про модулі, що спрощують їх інтеграцію у систему у багатьох САПР ПЛІС, які підтримують стандарт IP-XACT. Це такі метадані, як імена портів вводу-виводу, їх розрядність, код ідентифікації модуля, опис алгоритму, який реалізовано у модулі, ім’я файлу опису модуля, графічне зображення модуля, описане мовою SVG тощо. Наприклад, параметр nb, який задає розрядність даних, описується як:
<spirit:parameters>
<spirit:parameter maximum="32" minimum="8" type="int">
<spirit:name>nb</spirit:name>
<spirit:displayName>nb</spirit:displayName>
<spirit:value spirit:id="uuid_cd7f1ae6_bfb2">16</spirit:value>
<spirit:vendorExtensions>
<kactus2:vector>
<kactus2:left>15</kactus2:left>
<kactus2:right>0</kactus2:right>
</kactus2:vector>
</spirit:vendorExtensions>
</spirit:parameter>
</spirit:parameters>
Тоді структурну схему конвеєрного процесора ШПФ можна зібрати у графічному редакторі САПР, наприклад, в системі Kaсtus2, скомпілювати у VHDL-опис на структурному рівні та сконфігурувати у ПЛІС будь-якої підходящої серії та виробника. Слід додати, що Kaсtus2 – це проект з відкритим кодом, розроблений в університеті м. Тампере і оснований на стандарті IP-XACT. В табл. вказані результати синтезу таких процесорів ШПФ для кількості точок 64 і 128.
5. Висновки
Реалізація r-точкових модулів в ПЛІС забезпечує проектування високошвидкісних конвеєрних процесорів ШПФ з оптимізованим об’ємом апаратних витрат. Показано, що модуль ШПФ, який виконує r-точкове перетворення за r тактів має високу тактову частоту і невеликий обсяг апаратних витрат за рахунок
конвеєрних обчислень, властивості 6-вхідних ЛТ, а також застосування спеціалізованих блоків множення. Розроблені модулі ШПФ використані для створення конвеєрних процесорів ШПФ з довжиною перетворення 64, 128 і 256.
Виконується розробка WEB-застосування, яке забезпечує автоматичний синтез конвеєрних процесорів ШПФ на основі розроблених модулів з використанням стандарту IP-XACT. Деякі розроблені модулі ШПФ знаходяться у відкритому доступі для випробування та використання [5].
Перелік посилань
1. Lofgren J., Nilsson P. On hardware implementation of radix 3 and radix 5 FFT kernels for LTE systems // Proc. Norchip. −2011. −P. 1–4.
2. Quershi F., Garrido M., Gustafsson O. Unified architecture for 2, 3, 4, 5, and 7-point DFTs based on Winograd Fourier transform algorithm // Electronic Letters. −V.49. −N.5. −2013. −P.348 – 349.
3. Нусбаумер Г. Быстрое преобразование Фурье и алгоритмы вычисления сверток. −М.: Радио и связь. −1985. −248 с.
4. Сергиенко А. М., Симоненко В. П. Отображение периодических алгоритмов в программируемые логические интегральные схемы // Электрон. моделирование. – 2007. − T. 29, No 2. −С. 49−61.
5. Sergiyenko A., Usenkov O. Pipelined FFT/IFFT 128 points processor. − Режим доступу: http://opencores.org/project,pipelined_fft_128