Генетичне програмування опису конвеєра даних мовою VHDL

Д.т.н., с.н.с. Сергієнко А. М., к.т.н., доцент Романкевич В . О . ,
аспірантка Сергієнко А. А.
Національний технічний університет України
«Київський політехнічний інститут імені Ігоря Сікорського»

Abstract. The scheduling problem solving for the uniform synchronous dataflow graph (SDF) is considered. A method of the SDF scheduling is proposed, which is based on transforming uniform SDF into spatial SDF. The spatial SDF nodes have the coordinates of space, and the clock cycle, where and when the respective operator is computed. To search for the optimum mapping the spatial SDF to the structure, the genetic algorithm is proposed, which takes the matrix of the node coordinates as a chromosome.

Вступ. Багато алгоритмів, що обчислюють потоки даних, представлені за допомогою графів потоків даних (ГПД). Граф синхронних потоків даних (ГСПД) є особливим випадком ГПД, у якому кожен актор генерує і використовує сталу кількість даних протягом одного циклу алгоритму [1]. У цій роботі розглядаються лише однорідні ГСПД, хоча бувають і неоднорідні [1,2].

Проектування конвеєра даних має такі кроки, як вибір ресурсів, складання розкладу ГСПД, призначення операцій, розробка структури й схеми керування. Більшість методів складання розкладу для ГСПД розглядають ациклічний алгоритм. Добре відомі такі методи, як спискове планування (list scheduling), силове планування (force-directed scheduling). Для синтезу конвеєра застосовують модифікацію спискового планування, яка враховує циклічну природу ГСПД. Ефективний розклад знаходять за допомогою різних евристик та методу ресинхронізації (retiming) [1,3]. Процес проектування є складним, бо ці кроки залежать один від одного і мають різні цілі. Крім того, виконання загальних алгоритмів складання розкладу, є NP-повною задачею [4].

Отже, проектування конвеєрних обчислювачів є складним і потребує автоматизації. Для спрощення розробки конвеєрних схем та підвищення їхньої якості у роботі пропонується метод синтезу конвеєрного обчислювача за допомогою просторового ГСПД і його удосконалення з використанням генетичного алгоритму, завдяки чому спрощується пошук ефективного розкладу.

Просторовий ГСПД та складання розкладу для нього. У [5] описаний метод проектування конвеєра даних, у якому ГСПД подають у тривимірному просторі як конфігурація алгоритму K _G = (K, D, A). Тут K — це матриця векторів-вершин K _i, D — матриця векторів-ребер D _j, A — матриця інцидентності ГСПД. Координати k _i, s _i, t _i у векторі K _i = (k _i, s _i, t _i ) ^T відповідають типу оператора, номеру ПЕ та номеру такту відповідно. Таким чином, вектори K _i представляють теги, які задають властивості вершини ГСПД.

Просторовий ГСПД розділений на просторову конфігурацію K _GS = (K _S, D _S, A) та конфігурацію подій K _GT = (K _T, D _T, A), що представляють структуру конвеєра даних та його розкладу, відповідно. Тоді, вектори K _i = (k _i, s _i, t _i) ^T поділяють на вектори K _Si = (k _i,s _i) ^T координат ПЕ та вектори K _Ті = t _i виконань операторів. Часова частина D _Тj = t _i вектора D _j дорівнює затримці t _j обчислення i-ї змінної. Матриці K, D, A у коректній конфігурації K _G повинні задовольняти наступний ряд вимог і залежностей.

D = KA.      (1)
K = D _О A _О^-1      (2)
∀ K _i,K _j (K _i ≠ K _j , i ≠ j).      (3)
∀ K _i ,K _j (k _i = k _j, s _i = s _j ) ⇒ t _i not ≡ t _j mod L .      (4)
∀ D _j ≠ D _Dj (t _i ≥ 0),      (5)
K _i ,K _j ∈ K _p,q (k _i = k _j = p, s _i = s _j = q), |K p,q | ≤ L,      (6)
Σ_j b _{i, j} D _j = (0,0,0 )^T,      (7)

де D _О — матриця залежності векторів кістяка ГСПД; A _О — матриця інцидентності цього кістяка; L — період алгоритму; D _Dj = (k _j, s _j, –wL) ^T — вектор-ребро міжітераційної залежності, який позначають w затримками на w ітерацій алгоритму; K _p,q — множина операторів p-го типу, що відображаються в q-й ПЕ p-го типу (q =1,2,… q ^p _max ); b _i,j — елемент i-го рядка цикломатичної матриці ГСПД.

Пошук оптимізованого структурного рішення полягає у знаходженні матриці K, що мінімізує деякий критерій ефективності. Для конвеєрного блоку обробки даних притаманно те, що кожен оператор обчислюється протягом одного такту. За цих умов пошук ефективного розкладу полягає в наступному.

Координатам t _i векторів D _i ∈ D _О призначають значення t _i = 1, і матриця K _T формують за допомогою рівняння (2). Решту елементів матриці D _T одержують з виразів (1) та (7). Другу частину координат вектора K _i обчислюють з умов (3) – (7). У результаті, одержують циклічний розклад найскорішого призначення, оскільки кожен оператор виконується протягом одного такту.

Для мінімізації апаратних витрат пам’яті та мультиплексорів, а також спрощення VHDL-опису, виконують балансування ребер ГСПД. Для цього у ребра вставляють додаткові вершини затримок, доки не виконається умова D _j = (k _j, s _j, 1) ^T або D _j = (k _j, s _j, 0) ^T для будь-якого j.

Генетичне програмування просторового ГСПД. Як було показано вище, матриця K, наприклад, (9), містить всю інформацію як про розклад, так і про структуру конвеєрного блоку обробки даних. Завдяки цій властивості він може слугувати хромосомою, що задає одного індивіда в генетичному алгоритмі. Вектор K _i чи множина таких векторів, що належать до одного шляху у ГСПД, формує геном.

Початкове рішення отримують відповідно до правил, описаних вище. З цього рішення генерується перша популяція індивідів шляхом еквівалентних перетворень просторового ГСПД. Ці перетворення полягають у переміщенні векторів K _i у просторі, враховуючи умови (3)-(7). Потім повторюються наступні кроки алгоритму.

1) Створення нових індивідів означає створення копій матриці K.
2) Мутація полягає у випадковому виборі геномів в деяких індивідах, які вибираються випадковим чином, та їх заміна на нове випадкове значення, забезпечуючи коректність умов (3) — (7). Тасування (permutation) — це альтернативний метод мутації, коли міняються місцями два еквівалентні геноми одного індивіда.
3) Схрещування здійснюється шляхом обміну випадкових еквівалентних частин (множин геномів) двох генотипів.
4) Відбір ефективних індивідів відповідно до заданих критеріїв оптимізації.
5) Відбір найбільш ефективних індивідів до множини елітних особин, які зберігаються від мутації та схрещування.

Ці кроки формують життя одного покоління. Щоб одержати
оптимізоване структурне рішення, виконується еволюція до декількох сотень поколінь. Мутація, тасування та схрещування на прикладі підграфу просторового ГСПД ілюстровані на рис. 1.

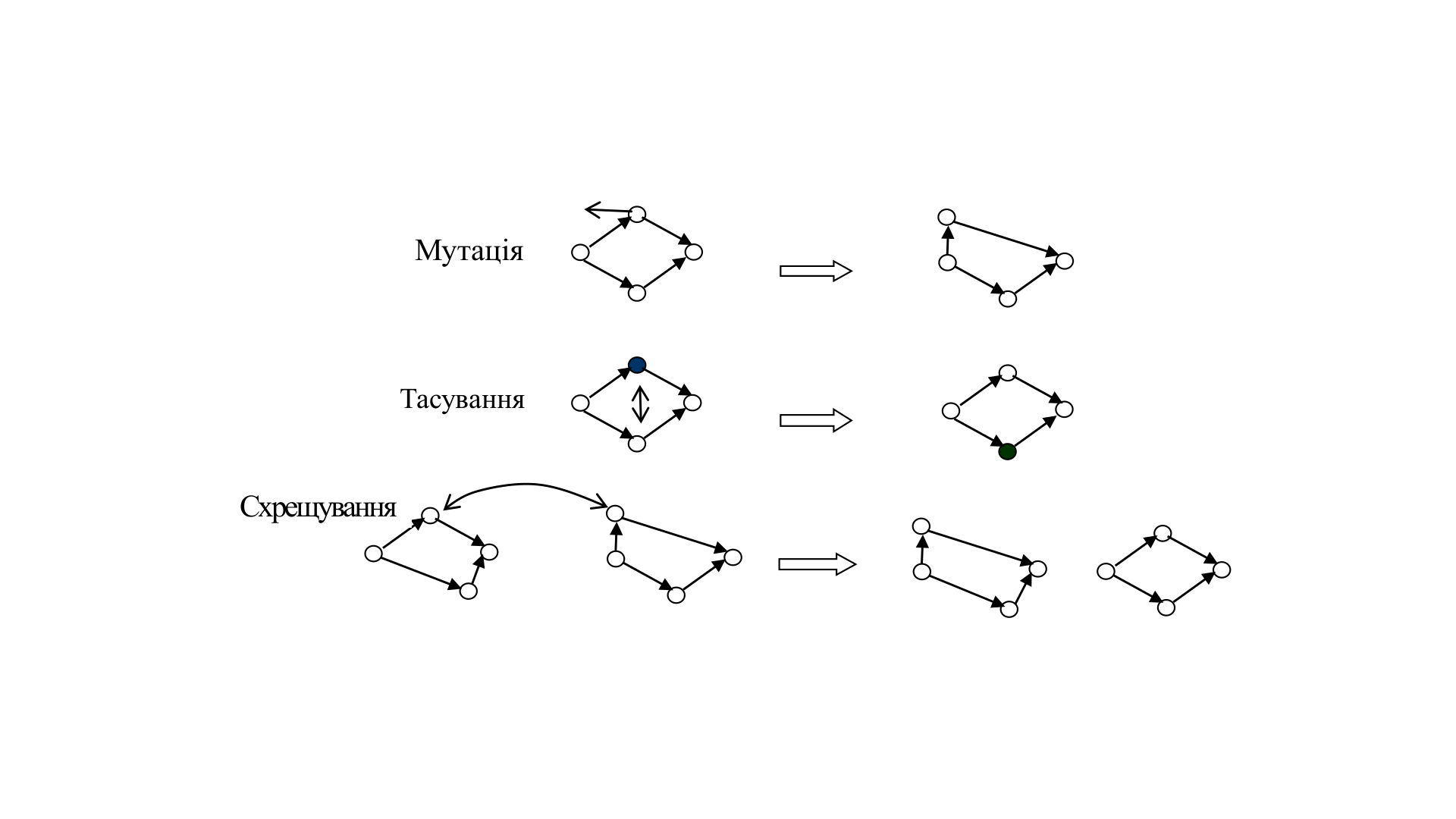
Рис. 1. Генетичні операції в просторовому ГСПД

Експериментальні результати. Спроектовано експериментальну програму для реалізації генетичного алгоритму на базі просторового ГСПД. Програма забезпечує ввід ГСПД, його графічне подання, програмну і ручну зміну ГСПД, контроль умов (3) — (7) та реалізацію генетичного алгоритму. Імовірності мутації, схрещування, відбору еліти тощо є регульованими. Результуючий ГСПД подається графічно та описаний мовою VHDL у стилі для синтезу. Попередня робота з цією програмою показала її придатність для оптимізації ГСПД.
Наприклад, після генетичної оптимізації ГСПД, який представлено в [6], критерій ефективності для нього дорівнює критерію рішення, яке одержане вручну. У найближчому майбутньому, актуальності набуде задача порівняння роботи експериментальної програми з результатами синтезу тестових проектів, вдосконалення алгоритму синтезу і впровадження його у практику.

Висновки. Запропонований генетичний алгоритм для складання розкладу ГСПД, який забезпечує проектування конвеєра даних із заданим періодом обробки даних і мінімізованими апаратними витратами. Метод ґрунтується на поданні ГСПД у тривимірному просторі та відображенні його у підпросторі подій та підпросторі структур. Ряд обмежень допомагає одержати циклічний розклад з періодом в L тактів і збалансовану завантаженість апаратних елементів. Приклад проектування конвеєра даних для рекурсивного фільтра другого порядку показує, що для малих ГСПД точний розв’язок задачі проектування можливий, і він не може бути вдосконалений за допомогою генетичного програмування. Генетичний алгоритм можна ефективно застосовувати для великих ГСПД, наприклад, таких як алгоритм ШПФ за великою основою [6].

Література

1. Lee E. A., Messerschmitt D. G. Synchronous Dataflow / E. A. Lee, D. G.
   Messerschmitt // Proc. IEEE, V.75, N9, 1987. — Р. 1235 – 1245.
2. O’Neil T. W. Retiming synchronous data-flow graphs to reduce execution time. / T. W. O’Neil, E. H. M. Sha // IEEE Trans. on Signal Processing, V.49, N10, 2001. — P. 2397 – 2407.
3. The Synthesis Approach to Digital System Design / Editors P. Micheli, U. Lauther, P. Duzy // Kluwer Academic Pub., 1992.
4. Robert Y., Vivien, F. Introduction to Scheduling / Y. Robert, F. Vivien // CRC Press, Taylor and Francis Group, 2010.
5. Sergienko A., Kanevski Ju., Maslennikov O., Wyrzykowski R. A method for mapping DSP algorithms into application specific structures / A. Sergienko, Ju. Kanevski, O. Maslennikov, R. Wyrzykowski, // Proc. 24-th Euromicro Conf. on Parallel and Distributed Processing, Euro-micro’98, Sweden, Vasteras, IEEE Press, V.1, 1998. — Р. 365 – 371.
6. Sergiyenko A., Serhienko A. Modules for Pipelined Mixed Radix FFT Processors / A. Sergiyenko, A. Serhienko // International Journal of Reconfigurable Computing, V. 2016, 1 – 7 (2016) — Article ID 3561317. — P. 1 – 7.