Конфігурована обчислювальна система для вирішення задач лінійної алгебри

⇓Завантажити PDF (українська)

Электронное моделирование. –2005. – Т. 27, –№1. –с.109−114.

А.Клименко, А.М.Сергієнко, Ю.Шевченко, С.Г. Овраменко

КОНФІГУРОВАНА ОБЧИСЛЮВАЛЬНА СИСТЕМА ДЛЯ ВИРІШЕННЯ ЗАДАЧ ЛІНІЙНОЇ АЛГЕБРИ.

Задачі лінійної алгебри все частіше зустрічаються в сучасній цифровій обробці сигналів, наприклад, при розпізнаванні образів, реалізації метода найменших квадратів. Для свого вирішення ці задачі потребують підвищеної точності обчислень. Тому вони, як правило, вирішуються на відносно дорогих мікропроцесорах з плаваючою комою.

Розвиток ПЛІС привів до появи кристалів з великою потенційною обчислювальною потужністю. Так, ПЛІС Xilinx Virtex2 має у своєму складі десятки апаратних блоків множення і блоков пам’яті, причому на один блок множення 18х18 розрядів припадає близько 200 еквівалентних конфігурованих обчислювальних блоків (ЕКЛБ). Але традиційна методика розробки проектів для ПЛІС оперує тільки з цілочисельною арифметикою, або з числами з фіксованою комою і не підтримує високоточні обчислення. А обчислювальні модулі для реалізації в ПЛІС операцій с плаваючою комою мають занадто великі затримки і апаратні витрати. Тому для вирішення задач линійної алгебри в ПЛІС необхідний пошук нових способів обчислень і алгоритмів, які адаптовані до цього обчислювального середовища.

При вирішенні вказаних задач багатократно використовується операція ділення, яка реалізується з великими апаратними витратами і затримкою, і є основним джерелом похибок обчислень. Існують алгоритми линійної алгебри, що основані на операції повороту комплексного вектора. В цих алгоритмах, як правило, не використовуються такі операції, як ділення, тому вони успішно виконуються в арифметиці цілих чисел. Так, в [1] описаний приклад реалізації в ПЛІС алгоритма QR- розкладання матриць методом Гівенса, що оснований на поворотах. Але при реалізації цих алгоритмів в нових ПЛІС їхні ресурси блоків множення використовуються нераціонально.

Для мінімізації похибок, затримок і апаратурних витрат на операцію ділення пропонується нетрадиційне представленння даних у вигляді дробів. Таке представлення приведено, наприклад, в [2] для цілочисельного вирішення задач з поліномами. При цьому число x представляється двомя цілими числами, перше з яких є чисельником n_x, а друге – знаменником d_x дробу, тобто x = n_x/d_x. Усі обчислення на перших N-1 ітераціях, наприклад, вирішення системи рівнянь, пропонується виконувати з даними у вигляді таких дробів. При цьому множення, ділення і додавання виглядає наступним чином:

x*y = n_x n_y /(d_x d_y) ; x/y = n_x d_y/(d_x n_y) ; x+y = (n_x d_y +n_y d_x )/ (d_x d_y).

У кінці останньої ітерації чисельники дробів діляться на знаменники звичайним діленням з одержанням результатів алгоритму. Таке представлення даних забезпечує як малі похибки обчислень, так і розширений динамічний діапазон в порівнянні з арифметикою цілих чисел, а також простоту реалізації в ПЛІС і високу швидкодію в порівнянні з пристроями з плаваючою комою. При досить великій розрядності дробів (більше 32) слід чекати, що точність обчислень перевищуватиме точність обчислень з плаваючою комою.

При розробці обчислювальної системи (ОС) для вирішення задач лінійної алгебри за базовий був прийнятий алгоритм обернення теплицевої матриці, що описаний в [3]. Перед відображенням в паралельну ОС, алгоритм обчислення матриці, оберненої до теплицевої, було описано і досліджено у вигляді поведінкової моделі на VHDL. При цьому був розроблений пакет Fract_Lib , який включає тип FRACTV, який представляє дріб з чисельника і знаменника і функції додавання, віднімання, множення і ділення над цим типом, функцію FRACT_REAL, що перетворює дріб в число з плаваючою комою а також константи nil=0/1 i one=1/1.

Теплицева матриця A загального вигляду задається двома векторами:

type ARRV is array(natural range <>)of FRACTV;
signal Af:ARRV(0 to nn);
signal Bf:ARRV(0 to nn);

де nn – порядок матриці, Af- перший рядок, Bf-останній рядок матриці A.

Алгоритм обчислення оберненої матриці полягає в обчисленні її першого Xf і останнього Yf стовпця, так як решту стовпців нескладно обчислити через ці стовпці. Масиви проміжних результатів були об’явлені як:

 signal Ff,Gf,Rf,Sf,Tf:arrv(0 to nn):=(others=>nil);

Алгоритм був записаний як наступний процес:

FRACT_INV: process(clk,rst)
     variable f,g,r,s,t:FRACTV ;
 begin
     if rst='1' then
        Xf(0)<=one/Af(0); Xf(0)<=one/Af(0);
     elsif rising_edge(clk)then
        f:=nil; g:=nil;
        for i in 0 to k-1 loop
          f:=f+Af(k-i)*Xf(i);
          g:=g+Bf(i+1)*Yf(i);
        end loop;
        r:=one/(one-f*g);s:=-r*f;t:=-r*g;
        Xf(0)<=Xf(0)*r;
        Yf(0)<=Xf(0)*t;
        Xf(k)<=Yf(k-1)*s;
        Yf(k)<=Yf(k-1)*r;
        for i in 1 to k-1 loop
          Xf(i)<=Xf(i)*r+Yf(i-1)*s;
          Yf(i)<=Xf(i)*t+Yf(i-1)*r;
        end loop; 
        Ff<=f;Gf<=g;Rf<=r;Sf<=s;Tf<=t;
      k<=k+1;
    end if;
 end process;

Процес обчислення починається по сигналу rst і закінчується через nn тактів синхросерії clk.

Для обчислення задач з теплицевими матрицями широко розповсюджені алгоритми Левінсона і Дарбіна [3]. Але ці алгоритми відрізняються нерегулярністю своїх графів залежностей і тому вони погано розпаралелюються. Приведений алгоритм відрізняється регулярністю і тому він добре відображається на структуру ОС у вигляді лінійки процесорних елементів (ПЕ), в якій ПЕ взаємодіють локально. Після відображення k-тi елементи векторів Af,Bf,Ff,Gf,Rf,Sf,Tf,Xf i Yf знаходяться в k-му ПЕ.

Арифметика дробів була використана в експериментальній паралельній ОС для вирішення задач з теплицевими матрицями. Паралельна ОС має кільцеву структуру, яка може бути змінена на будь-яку структуру, завдяки реконфігурації ПЛІС. ПЕ взаємодіють між собою через буфери даних і механізм переривань з високою швидкодією.

За основу процесорного елемента паралельної ОС було взяте ядро мікропроцесора RISC_ST, що описане в [4]. Це ядро складається з базового ядра і апаратного прискорювача. Апаратний прискорювач реалізує розширення команд з арифметикою дробів та інших операцій, що часто використовуються при цифровій обробці сигналів. При цьому виконання множення і ділення дробів триває один такт, а їхнє додавання – два такта. Перед записом в пам'ять чисельник і знаменник результата нормалізуються шляхом зсуву на 0, 1 або 2 розряди вліво. Загальний об'єм обладнання одного ПЕ при реалізації даного алгоритму складає 380 ЕКЛБ, 2 блока множення і 2 блока ОЗП, а тактова частота досягає 80 МГц при конфігурурованні в ПЛІС Xilinx Virtex2.

Методика розробки застосування для паралельної ОС складається з трьох етапів. На першому етапі розробляються на мові асемблера і транслюються програми для ПЕ за допомогою асемблера процесора RISC_ST, що зкоригований для трансляції додаткових команд. Одержані програми відлагоджуються і тестуються на моделі ОС за допомогою системи Active HDL. При трансляції невикористані коди команд ПЕ і адреси даних і переривань фіксуруються асемблером.

На другому етапі генерується опис ПЕ і паралельної ОС в цілому на VHDL, в якому відсутні невикористані вузли і елементи пам"яті моделі ПЕ. Завдяки цьому одержуються мінімізовані апаратні витрати кожного ПЕ. Кожна зтрансльована програма вкладається в ОЗП програми відповідного ПЕ. На третьому етапі всі моделі ПЕ підключаються до VHDL – проекту, який транслюється в файл конфігурації цільової мікросхеми ПЛІС.

Паралельна ОС з N=10 ПЕ відображається в ПЛІС Xilinx XCV2-1000. За допомогою цієї ОС обернена матриця розмірності N=10 (точніше – її перший і останній стовбці) знаходиться за 1.23 мкс., не рахуючи ввод-вивід начальних даних і результатів. Таким чином, середня продуктивність ОС досягає 172 млн. операцій в сек., таких як складання, множення і ділення, які еквівалентні операціям з плаваючою комою.

Для приймання рішення про доцільність використання розробленої ОС
була виконана оцінку похибок обчислень в ній. На рис. показані графіки залежності похибки результатів обчислень від розмірності матриці N і від розрядності даних n.

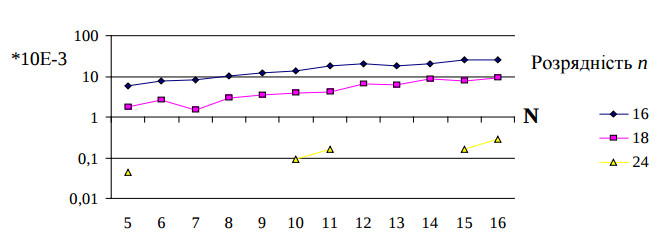
Кожне дане для графиків одержано при оберненні 500 випадкових невироджених теплицевих матриць і осередненні похибок результатів. Завдяки підвищенній до n=18 розрядності блоків множення ПЛІС, одержується похибка обчислень близько 0,5%, що майже в 4 раза менше, ніж при реалізації цього алгоритму в 16-розрядному сигнальному мікропроцесорі. Такої точности досить для вирішення багатьох задач цифровоі обробки сигналів, таких як адаптивна фільтрація, лінійне передбачення і т.і.