Методика проектирования цифровых фильтров с помощью VHDL

⇓Загрузить PDF (рус.)

Моделювання та інформаційні технології. Зб. наук. праць. Ін-т проблем моделювання в енергетиці ім. Г.Е. Пухова. НАНУ.-2002.-Вип. 12.-С. 99-107.

А. М. Сергиенко

МЕТОДИКА ПРОЕКТИРОВАНИЯ ЦИФРОВЫХ ФИЛЬТРОВ С ПОМОЩЬЮ VHDL

В последнее время уделяется большое внимания автоматизации проектирования структур цифровых фильтров (ЦФ), вызванное развитием технологии разработки систем на кристалле, которая требует минимизации аппаратурных затрат, энергопотребления и сроков проектирования. В статье предлагается методика проектирования ЦФ, упрощающая отображение алгоритма цифровой фильтрации в структуру ЦФ, описанную на языке VHDL.

Графы синхронных потоков данных (ГСПД) считаются наиболее удобной формой представления алгоритмов цифровой обработки сигналов, в том числе алгоритмов цифровой фильтрации [1,2]. В них вершины представляют собой арифметические операторы, а дуги – передачи данных между ними. Если дуга ГСПД нагружена целым числом d, то она означает, что данные передаются по ней с задержкой на d циклов алгоритма. ГСПД часто используются при проектировании ЦФ, благодаря своей простоте и тому, что для них всегда можно составить статическое расписание выполнения операторов [2].

Наиболее распространен подход к структурному проектированию ЦФ, согласно которому с помощью единичного отображения вершины ГСПД отождествляются конкретным арифметическим блокам (сумматорам, умножителям), дуги – линиям связи между блоками, а нагруженные дуги – регистрам задержки. При этом получают ЦФ с максимальным быстродействием и высокими аппаратурными затратами. Такие структуры выполняют алгоритм фильтрации с длительностью цикла L = 1 такт.

Согласно другому подходу, сначала выбирают набор ресурсов (блоков умножения, сложения), затем составляют расписание выполнения вершин-операторов ГСПД на этих ресурсах. Связи между блоками, число и место включения регистров данных определяют окончательно после составления расписания. Тогда период выполнения алгоритма L>1 и чаще всего L>>1. Возможности подхода ограничены из-за низкого быстродействия результирующих структур или большого отношения аппаратурные затраты – быстродействие, так как часто не достигается желаемая степень оптимизации структурных решений.

В работе [3] предложен метод структурного проектирования ЦФ, основанный на отображении ГСПД, представленного в индексном пространстве, в подпространства структур и событий. Основным преимуществом этого метода является то, что структура ЦФ и расписание выполнения операторов находятся почти одновременно, а не на отдельных этапах, благодаря чему упрощается оптимизация структурного решения.

В данной статье предлагается методика проектирования ЦФ на основе метода [3], причем результирующее структурное решение фильтра получается как описание ГСПД, представленного в индексном пространстве, с помощью языка VHDL.

Метод структурного проектирования ЦФ, описанный в [3], заключается в следующем. Предполагается, что структура ЦФ состоит из множества процессорных элементов (ПЭ), связанных между собой согласно графу структуры ЦФ. ПЭ включает в себя АЛУ определенного типа (умножитель, сумматор и т.п.) с регистром результата на его выходе (или с цепочкой регистров типа FIFO) и мультиплексорами входных данных на его входе. Допускается подключение выхода регистра ко входу мультиплексора этого же ПЭ. ПЭ выполняет операцию над входными данными с записью результата в регистр не более, чем за один такт. Если ПЭ не имеет регистра, то считается, что операция выполняется без задержки.

ГСПД представляется в трехмерном целочисленном пространстве в виде конфигурации алгоритма (КА) K_G = (K,D,A), где K – матрица векторов-вершин, соответствующих операторам алгоритма, D – матрица векторов-дуг, отвечающих непосредственным информационным связям между операторами, A – матрица инцидентности ГСПД. В векторе-вершине K_i =<k_i,l_i,t_i>координаты k_i,l_i,t_i равны, соответственно, типу оператора (например, k = 1 – умножение), номеру процессорного элемента, где выполняется данный оператор и такту, в котором выполняется данный оператор.

Различным эквивалентным структурным решениям ЦФ соответствуют различные матрицы К. Поиск оптимального структурного решения или КА заключается в нахождении такой матрицы К, которая минимизирует заданный критерий качества. При поиске эффективных структурных решений необходимо руководствоваться следующими закономерностями.

КА является корректной, если в матрице К нет двух одинаковых векторов, т.е.

∀ K_i,K_j (K_i≠ K_j, i≠ j ) .

Расписание выполнения алгоритма является корректным, если операторы, отображаемые в один и тот же ПЭ, выполняются в различных тактах, т.е.

∀ K_i,K_j(k_i=k_j, l_i =l_j ) ⇒ t_i ≠ t_j mod L.

Однотипные операторы следует отображать в ПЭ того же типа, т.е.

K_i,K_j∈K_p,q(k_i=k_j=p, l_i =l_j =q), | K_p,q| ≤ L,

где K_p,q – множество векторов- вершин операторов p– го типа, отображаемых в q-й ПЭ p- го типа (q=1,2,… q^p_max).

Если в ГСПД есть циклы межитерационной зависимости, то должна быть равна нулю сумма векторов-дуг D_j, входящих в любой из циклов графа, т.е. для i-го цикла

∑ b_i,j D_j = 0,

где b_i,j – элемент i-й строки цикломатической матрицы ГСПД. Такие циклы всегда существуют в рекурсивных фильтрах, причем обратные векторы – дуги D_Вj=<0,0,-iL> означают задержку, равную i циклов (итераций).

В качестве критериев оптимальности можно принять период выполнения алгоритма Q_T =L и cумму взвешенных количеств ПЭ различного типа:

Q_S =∑ С_p q^p_max,

где С_p – аппаратная стоимость ПЭ p-го типа, например, выраженная в числе эквивалентных вентилей. Также одним из критериев может служить суммарное количество входов ПЭ Q_SМ в результирующей структуре, которое приблизительно пропорционально сложности их входных мультиплексоров, а также отражает сложность линий связи. Как интегральный критерий качества можно принять величину Q = Q_T(Q_S +С_M Q_SM), которая равна числу вентилей в ЦФ, приведенному к одному Герцу частоты дискретизации сигнала при заданной тактовой частоте, где СМ – приведенная сложность мультиплексора.

Исходными данными принимаются ГСПД заданного алгоритма фильтрации и период его выполнения L. Процесс получения эффективной конфигурации алгоритма включает два этапа. На первом этапе вершины-операторы ГСПД вместе с дугами размещаются в трехмерном пространстве как множества векторов K_i и D_j, соответственно, с учетом всех условий, приведенных выше. При этом выполняется минимизация числа ПЭ путем выполнения требования | K_p,q|→L.

На втором этапе выполняется уравновешивание КА. Ациклический граф считается уравновешенным, если все маршруты между любыми двумя вершинами имеют одинаковую длину. Для уравновешивания КА рассматривается ациклический подграф ГСПД, представляющий собой исходный ГСПД без обратных векторов – дуг D_Вj и во все его дуги включаются промежуточные вершины операторов задержки. В результирующей уравновешенной КА все векторы-дуги, кроме обратных векторов – дуг, равны D_j=<a_j, b_j, 1> или D_j=<a_j, b_j, 0> . При этом вершины-операторы образуют ярусы, расстояние между которыми по координате времени t равно 1.

После уравновешивания КА выполняется ее оптимизация путем взаимных перестановок векторов-вершин из одного яруса с целью минимизации числа регистров и числа входов мультиплексоров в результирующей структуре и/или с применением других стратегий, например, ресинхронизации или алгоритма левого края, которые минимизируют суммарное число регистров.

Полученная оптимизированная КА отображается в граф структуры ЦФ путем склеивания векторов-вершин с одинаковыми координатами k, l . КА преобразуется в расписание выполнения операторов, используя то свойство, что момент выполнения оператора, соответствующего K_i = <k_i,l_i,t_i>, равен t_i.

Рассмотрим синтез логических схем из VHDL-описания как процесс отображения алгоритма. Одним из основных этапов разработки цифровых схем является их описание на уровне регистровых передач на таком языке, как VHDL или Verilog с дальнейшей автоматической трансляцией в логическую схему с помощью компилятора – синтезатора. При такой компиляции выполняется отображение операторов языка в конкретные функциональные блоки, описанные на логическом уровне. Например, оператор сложения отображается в схему сумматора. При этом используется ряд способов автоматической оптимизации.

Способ разделения ресурсов (resourсe sharing) позволяет отождествить несколько однотипных операторов, которые не могут быть выполнены одновременно, одному функциональному блоку. Для того, чтобы компилятор распознал случай разделения ресурсов, можно использовать конструкцию case языка VHDL, как например:

case sel is
   when 0 => y <=st(a,b);
   when 1 => y <=st(a,c);
   when others => y <=st(b,c);
end case;

Эта конструкция отображается в функциональный блок, выполняющий функцию st , ко входам которого подключены мультиплексоры, пропускающие операнды a,b или с в зависимости от сигнала – селектора sel.

Вызовам одной функции в конструкции case отвечают некоторые вершины графа алгоритма. Тогда выполнение минимизации с помощью разделения ресурсов означает склеивание этих вершин. Если состояния сигнала – селектора означают различные такты периода выполнения алгоритма, то результирующий функциональный блок будет выполнять данную функцию в соответствующих тактах этого периода.

На основе приведенных свойств языка VHDL и особенностей компиляторов-синтезаторов можно разработать методику описания алгоритма цифровой фильтрации в виде VHDL –модели, которая будет транслироваться в минимизированную логическую схему ЦФ. При этом результирующая структура ЦФ получается в неявном виде, так как чтобы получить граф структуры, необходимо выполнить склеивание вершин операторов, отображаемых в один ПЭ. Как раз эту задачу выполняет компилятор синтезатор.

Методика заключается в выполнении трех этапов. Исходными данными для проектирования ЦФ являются ГСПД алгоритма ЦФ и период L вычислений. На первом этапе вершины-операторы ГСПД вместе с дугами размещаются в трехмерном целочисленном пространстве с получением КА, учитывая вышеприведенные закономерности и минимизируя количество таких ресурсов, как сумматоры и особенно, умножители.

На втором этапе выполняется уравновешивание КА с минимизацией числа регистров и числа входов мультиплексоров в результирующей структуре. При выполнении первого и второго этапов эффективно использовать программный комплекс Parlab [4], который позволяет автоматически генерировать уравновешенную КА с учетом периодичности вычислений и затем вручную улучшать решение.

В результате этого этапа формируются L множеств операторов, причем в m–м множестве К_m содержатся операторы, соответствующие таким векторам-вершинам, что K_i = <k_i,l_i,t_i>, m = t_i mod L , m= 0,1,…, L-1. Для этого в результирующем ГСПД, представленном в трехмерном пространстве, выделяются ярусы, которые отстают друг от друга на L тактов по оси t и вершины этих ярусов образуют множества К_m. Также формируются множества K_p,q векторов-вершин операторов p- го типа, отображаемых в q-й ПЭ и каждому из этих множеств отождествляется уникальное имя, например, upq. Таким образом, каждому из операторов, обозначенному вектором K_i, ставится в соответствие единственная пара: <upq, t >, где upq означает имя переменной (сигнала), хранящейся в соответствующем регистре ПЭ, а t – номер такта, в котором выполняется присваивание этой переменной.

На третьем этапе получается структурное решение ЦФ как описание оптимизированной КА на языке VHDL. Это решение пердставляет собой архитектуру VHDL, состоящую из операторов процесса синхронизации и процесса функционирования ЦФ.

Вначале описывается процесс синхронизации, который генерирует фазы алгоритма cycle = 0,1,…, L-1. Затем описывается процесс функционирования
ЦФ следующим образом. Отдельными операторами описывается присваивание переменным, которые соответствуют обратным векторам – дугам D_Вj.

В пределах действия условного оператора, который описывает изменение состояний по фронту синхросерии, ставится оператор case cycle, в котором
размещено L альтернатив от 0 до L-1. При этом в t – й альтернативе ставятся операторы присваивания сигналу upq результата соответствующей операции, отмеченной парой <upq, t >.

Результирующая VHDL – модель ЦФ может быть протестирована и синтезирована обычным порядком. Следует отметить, что многие компиляторы-синтезаторы не выполняют оптимизацию разделения ресурсов для таких операций, как умножение. В этом случае процесс функционирования ЦФ следует заменить на эквивалентный процесс, который описывает отображение фрагмента алгоритма в умножитель с мультиплексорами на его входах. Кроме того, некоторые компиляторы-синтезаторы могут не минимизировать цепочку тождественных присваиваний, как например, a:=b; c<=a, поэтому такие цепочки следует минимизировать вручную.

Рассмотрим пример проектирования режекторного рекурсивного фильтра с передаточной функцией:

H(z)= 1 + (a – bz^-1 + z^-2)/(1 − bz^-1 + az^-2).

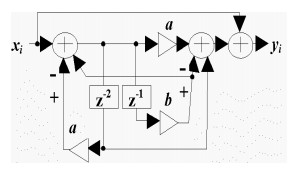
Его ГСПД показан на рис. 1.

На рис.1 кружочками представлены операторы сложения, треугольниками — операторы умножения на константу, прямоугольниками – дуги, нагруженные задержками на 1 и 2 цикла. Так как число умножений в цикле равно 3 и длительность критического пути составляет сумму задержек двух двухвходовых сумматоров и одного умножителя, длительность цикла выбрана равной L=3. Тогда в результирующей структуре следует ожидать наличие не более чем одного умножителя и двух сумматоров.

После первого и второго этапов проектирования получается уравновешенная КА с минимизированным числом регистров входов мультиплексоров. На рис.2. показана эта КА, полученная с помощью программного комплекса Parlab. В ней по горизонтальной оси отмечены значения t mod L, а по вертикали – имена переменных, соответствующих результатам различных операций, т.е. координатам k и l. Кружками обозначены векторы- вершины операторов задержки, отображаемых в регистры, а прямоугольниками – вершины операторов сложения и умножения. Пунктирными стрелками обозначены обратные векторы – дуги D_Вj длины 1 и 2 цикла.

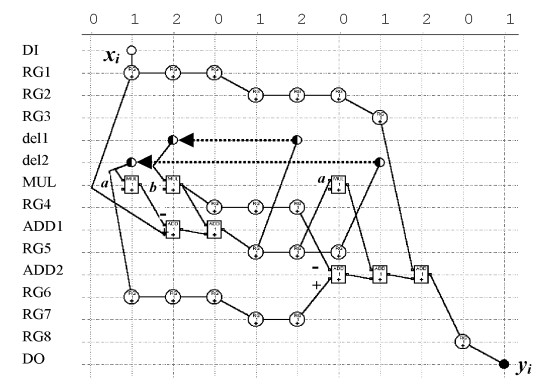
Анализ КА показывает, что аппаратные затраты результирующего ЦФ составляют 1 умножитель, 2 сумматора, 11 регистров и 7 входов мультиплексора. В результате выполнения третьего этапа получим следующую VHDL- программу.

entity REJECT2 is
   port(CLK,RST: in BIT;
   DI: in INTEGER range -2**9 to 2**9-1;
   DO: out INTEGER range -2**9 to 2**9-1);
end REJECT2;
architecture allpass2 of REJECT2 is
   constant a:INTEGER:=507;constant b:INTEGER:= 991;
   signal cycle: INTEGER range 0 to 3;
   signal RG1,RG2,RG3,RG4,RG5,RG6,RG7,RG8,ADD1,ADD2
     : INTEGER range-2**9 to 2**9-1;
   signal MUL :INTEGER range -2**19 to 2**19-1;
begin
CT3:process(CLK,RST) begin
      if RST='1' then cycle<=0;
         elsif CLK='1' and CLK'event then
         cycle<=cycle+1;if cycle=2 then cycle<=0;end if;
      end if;
 end process;
DP:process(CLK,RST)
    variable del1,del2,c,t: INTEGER;
 begin
    del1:=RG5; del2:=RG5;
 if RST='1' then
    RG1<=0;RG2<=0;RG3<=0;RG4<=0;RG5<=0;RG6<=0;
    RG7<=0;RG8<=0;ADD1<=0; ADD2<=0; MUL<=0;
 elsif CLK='1' and CLK'event then
    case cycle is
       when 0 =>RG1<=RG1; RG2<=RG2; ADD1<=ADD1+MUL;
          c:=a; t:=RG5; ADD2<=RG7-RG4; RG4<=MUL;
          RG5<=RG5;RG6<=RG6; RG8<=ADD2;
       when 1 => RG1<= DI; RG2<=RG1; RG3<=RG2;
          c:=a; t:=del2; RG6<=del2; RG4<=RG4;
          RG5<=ADD1; RG7<=RG6; ADD2<=ADD2+MUL;
       when others => RG1<=RG1;RG2<=RG2;ADD1<=RG1-MUL;
          c:=b;t:=del1;ADD2<=ADD2+RG3; RG6<=RG6;
          RG4<=RG4; RG5<=RG5; RG7<=RG7;
    end case;
   MUL<=c*t/2**15;
  end if;
 end process;
 DO<=RG8;
end allpass2;

Индентификаторами СТ3 и DP поименованы соответственно процессы синхронизации и функционирования ЦФ. Так как синтезатор Synopsys пакета Xilinx Foundation не выполняет разделение такого ресурса, как умножитель, то оператор присваивания результата умножения MUL вынесен за пределы оператора case. Для иллюстрации формального перехода от КА к программе, в ней не минимизированы операторы присваивания.

При тестировании этого ЦФ в среде ActiveHDL 5.1. построен график амплитудо-частотной характеристики, представленный на рис.3. Данный фильтр занимает 147 логических таблиц (ЛТ) в ПЛИС Xilinx VirtexЕ и функционирует с максимальной тактовой частотой 89 МГц. Он может фильтровать сигнал с частотой дискретизации 29,7 МГц при удельных аппаратурных затратах Q = 4,95 ЛТ/МГц. Для сравнения, этот фильтр, реализованный по обычной методике, при L=1 такт, имеет аппаратурные затраты 251 ЛТ и максимальную тактовую частоту 32 МГц, а его удельные аппаратурные затраты 7,84 ЛТ/МГц, т.е. на 58% больше.

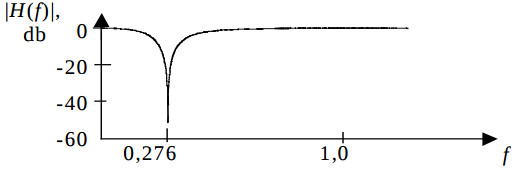
Итак, предложенная методика проектирования цифровых фильтров с помощью VHDL отличается высоким уровнем формализации и высоким качеством получаемых ЦФ, которые имеют минимизированные аппаратурные затраты и длительность такта при заданном цикле вычислений L. Структурное решение ЦФ, описанное на языке VHDL представляет собой проект, готовый к исполнению в ПЛИС или заказной СБИС. Это решение получается, минуя построение самой структуры, благодаря чему его оптимизация выполняется направленно и имеет меньшую трудоемкость. Уровень формализации методики достаточен для ее автоматического исполнения. Методика может быть усовершенствована для отображения алгоритмов более общего вида, чем алгоритмы цифровой фильтрации.

1. Оппенгейм А.В., Шафер Р.В. Цифровая обработка сигналов. М.: "Связь". –1979. – 416с.

2. Ли Е.А., Мессершмитт Д.Г. Вычисления с синхронными потоками данных. ТИИЭР. -1987. -Т75. -№9. –с.107-119.

3. Каневский Ю.С., Логинова Л.М., Сергиенко А.М. Структурное проектирование рекурсивных цифровых фильтров. Электронное моделирование. –1995. -№3. –с. 18-22.

4. Kanevski Ju.S., Sergienko A.M., Guzinski A. A Method for Mapping Unimodular Loops into Application Specific Parallel Structures. Proc. of the 2-nd Intern. Conf. "Parallel Proc. and Appl. Math. PRAM'97" (Zakopane, Poland, 1997).-p. 362-371.

⇓Загрузить PDF (рус.)