Отображение алгоритма QR-разложения Гивенса в многопроцессорную систему
Электрон. моделирование. – 2004. – T.26. – №5. – С.43-53.
А.М. Сергиенко, канд. техн. наук
(Национальный технический университет Украины “КПИ”)
Отображение алгоритма QR-разложения методом Гивенса в многопроцессорную систему.
QR-разложение матриц методом Гивенса широко применяется для решения задач
линейной алгебры. В результате применения метода синтеза систолических процессоров путем укрупнения графов структур и конвейеризации вычислений получена вычислительная схема, реализующая алгоритм Гивенса. В приведенных примерах многопроцессорных вычислительных систем (ВС), реализующих эту схему на базе сигнальных микропроцессоров и программируемых логических интегральных схем, достигнуты минимальные простои оборудования и максимальное ускорение вычислений, которое в 1,5 раза выше, чем у схемы Самеха−Кука и значительно выше, чем при использовании методов LU-разложения. Реализация этой схемы в мультипроцессорных ВС на суперскалярных микропроцессорах может дать большой прирост производительности.
QR-розкладання матриць методом Гiвенса широко використовується для вирішення задач лінійної алгебри. В результаті використання методу синтезу систолічних процесорів шляхом укрупнення графів структур и конвейеризації обчислень одержана обчислювальна схема, що реалізує алгоритм Гівенса. В приведених прикладах багатопроцесорних обчислювальних систем (ОС), що реалізують цю схему на базі сигнальних мікропроцесорів і программованих логічних інтегральних схем, досягнуті максимальні завантаження процесорних елементів і прискорення обчислень, яке в 1,5 рази вище, ніж у схеми Самеха−Кука і значно вище, ніж при використанні методів LU-розкладання. Реалізація цієї схеми в сучасних ВС на суперскалярних мікропроцессорах може дати великий приріст їхньої продуктивності.
QR-разложение матриц широко применяется для решения задач линейной алгебры.
В отличие от методов LU-разложения, исключения Гаусса [1], методы QR-разложения более трудоемкие, но они численно устойчивы и имеют высокую степень распараллеливания вычислений [2,3]. При QR-разложении методом Гивенса матрица A последовательно умножается на матрицы вращения Гивенса Pi,j, в результате чего аннулируются поддиагональные элементы матрицы A. Например, если необходимо аннулировать элемент a1,2, то после преобразования получим: A’ = P1,2*A, где P1,2 – слабозаполненная матрица, в диагонали которой стоит ортогональная матрица P = ((с,-s)Т,(s,c)Т) и единичная матрица, причем
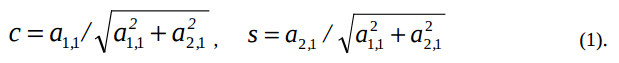
Благодаря естественному параллелизму алгоритма Гивенса, одновременно можно аннулировать несколько элементов матрицы. Поэтому при реализации этого алгоритма в паралельных вычислительных системах (ПВС) достигается большая загруженность их процессорных элементов (ПЭ) [2, 12]. Наибольшим параллелизмом обладает алгоритм, называемый вычислительной схемой С Самеха-Кука, структура которой S представляет собой двумерную решетку ПЭ [2,3].
Работы [4,…,11] посвящены отображению алгоритма Гивенса в систолические структуры. Метод структурного синтеза систолических процессорных матриц [1, 13] и другие аналогичные методы, например [15], предполагают, что операторы, реализуемые в ПЭ выполняются за один такт или шаг алгоритма. В структурных схемах ПВС, реализующих алгоритм Гивенса [4, 6,…,12], также считается, что различные операторы выполняются за одинаковое время, равное времени выполнения самого сложного оператора, вычисляющего формулу (1).
В работе [5] для отображения алгоритма Гивенса в ПЭ с конвейерными умножителями и сумматорами предлагается применить приемы увеличения количества тактов в цикле (slowdown), оптимизации расписания выполнения операторов (retiming) и объединения соседних операторов в укрупненный оператор. Недостатком полученной структуры является низкая степень параллелизма и как результат, невысокая предельная производительность.
В данной работе выполнен ряд отображений алгоритма Гивенса в структуру двумерной процессорной матрицы с целью получения максимальной загруженности ПЭ при высоком коэффициенте ускорения алгоритма. Отображение алгоритма выполняется в соответствии с методом синтеза систолических процессоров, представленным в работах [1,13]. Этот метод модернизирован с целью выполнения отображения в параллельные структуры с конвейерными ПЭ, имеющими задержку более одного такта, метод проектирования которых описан в работах [16-19].
Алгоритм Гивенса выполняется над матрицей исходных данных a[i, j], i, j = 1,…,n. Он предполагает периодическое исполнение оператора первого типа :(c,s,b) = f1(x,y) , выполняющего вычисления согласно формулам (1), а также b =cx+sy и второго типа (a,b) = f2(c,s,x,y), реализующего операцию вращения Гивенса над парой одноименных элементов соседних строк:
a = −sx+cy; b = cx+sy; x =a[i−1, j], y = a[i, j].
Следуя методу синтеза систолического процессора, решетчетый функциональный граф (РФГ) алгоритма Гивенса представляется в трехмерном итерационном пространстве Z3. При этом каждому исполняемому оператору соответствует вектор-вершина K=(i,j,k)T графа алгоритма. Переменной, передаваемой между p-м и q-м операторами соответствует вектор-дуга информационной зависимости Dl = Kq−Kp. Неповторяющиеся векторы информационной зависимости Dl образуют характеристическую матрицу D, которая для данного алгоритма равна:
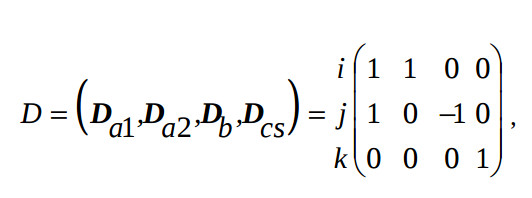
где векторы Da1, Da2, Db, Dcs отвечают передаче переменной a[i, j, k] при j≠n, a[i,n,k] , b[i,j,k], а также переменных c[i,j,k] и s[i,j,k], соответственно, причем a[0,j,k] = a[j,k] – исходные данные.
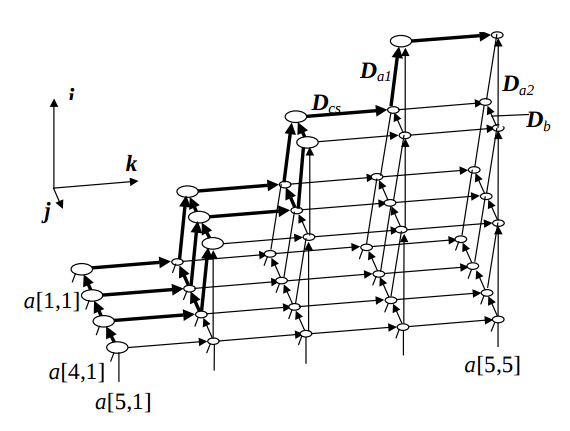
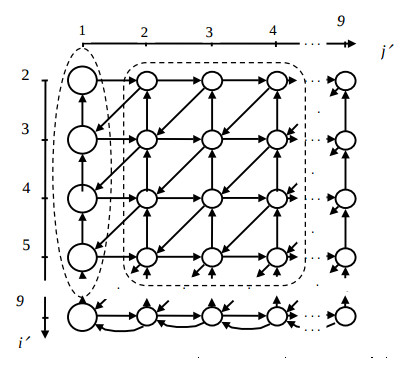
На рис. 1 показан РФГ алгоритма для n = 5, на котором большим и маленьким кружком обозначены операторы первого и второго типа, соответственно. Количество вершин операторов первого типа равно W1 = n(n−1)/2, а вершин операторов второго типа – W2 ≈ (n-1)3/3+(n-1)2/2.
В зависимости от алгоритма и элементной базы ПЭ, время вычисления оператора f1 в QВ = 3,…,20 раз больше, чем время вычисления оператора f2. Поэтому если не учитывать коэффициент относительной сложности QВ, то неизбежна низкая загруженность ПЭ процессорной матрицы. Чтобы минимизировать простои ПЭ, а также получить выигрыш за счет специализации ПЭ, необходимо, чтобы операторы f1 и f2 выполнялись в различных ПЭ, соответственно первого и второго типа.
Структуру S1 для структурной схемы C1, обладающей этим свойством, получают путем отображения графа алгоритма на гиперплоскость структур, перпендикулярную вектору KН = (1,0,1)T. Тогда матрица пространственной компоненты преобразования равна PS =((0,−1)Т,(1,0)Т,(0,1)Т).
Оператор, обозначенный Ki , выполняется в ПЭ с координатами PSKi, а матрица векторов-дуг межпроцессорных связей равна ∆S = PSD. Полученный граф структуры для n = 9 показан на рис. 2. Данная структура является базовой, поскольку остальные структуры получаются путем её трансформации.
Временная компонента функции отображения равна PT = (2, −1, 1). Тогда, если не учитывать различие в сложности операторов первого и второго типа, момент начала выполнения вершины-оператора K будет равен t = PTKQB+(n−3)QB.
Основные характеристики, полученной структурной схемы C1 можно оценить следующим образом. Время выполнения алгоритма равно:
Ta =(max(PT∗Kl) − min(PT∗Kl)+1) QB=PT∗(n−1,n,n)T-PT∗ (1,n,1)T+1 = (3n − 4)QB.
Сложность алгоритма в количестве операций второго типа можно оценить как
W = W1СB+W2 ≈ (n −1)3/3+(QB+1)(n −1)2/2 ≈ n3/3.
Тогда коэффициент ускорения выполнения алгоритма на параллельной структуре равен Ky = W/Ta ≈ n2/(9QB).
Средняя загруженность ПЭ равна η = Ky/M, гдеM – количество процессоров в структуре, т.е. η ≈ 1/(9QВ). Следует отметить, что параметры коэффициента ускорения и средней загруженности совпадают с этими параметрами для схемы Самеха−Кука [2], которые можно принять как эталонные. Также для сравнения, структурная схема двумерного матричного процессора для решения LU-разложения методом Гаусса с частичным выбором ведущего элемента имеет Ky = 2n/3 и η = 2/(3n) [1], т.е. алгоритма Гивенса предпочтительнее для реализации в ПВС с массивным параллелизмом.
Характеристики вычислительной схемы C1 и других полученных в данной работе вычислительных схем сведены в таблицу. Согласно анализу задержки между выполнением соседних операторов второго типа, ПЭ второго типа простаивают долю времени, равную (QB −1)/QB, т.е. схема С1 – неоптимальна.
Пусть QB – целое число. Если отображать до QB соседних операторов второго типа с одинаковой координатой k в один ПЭ, то результирующая структура S2, может быть получена из структуры S1 объединением соседних QB вершин ПЭ. Её размеры M1∗M2 при произвольном QB равны : M1 = n −1 и M2 = ](n−1)/ QB[+1.
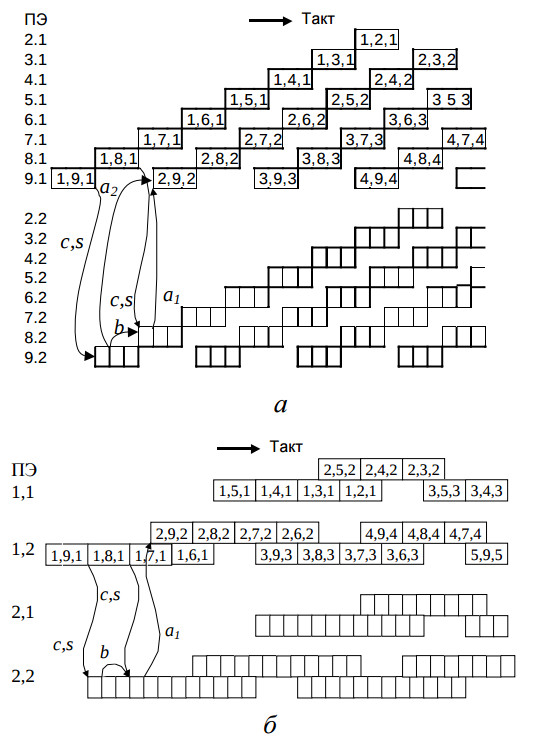
Матрица временного отображения результирующей вычислительной схемы C2 равна PT = (2QB,−QB,1). Временная диаграмма загруженности процессоров вычислительной схемы C2 показана на рис. 3а. Местоположение прямоугольников диаграммы означает номер ПЭ и временной интервал выполнения операторов, координаты которых указаны внутри прямоугольников. Вычислительная схема C2 имеет приблизительно в QB раз меньшее количество процессоров и приблизительно в 1,5 раза меньшее время вычисления алгоритма, по сравнению с вычислительной схемой C1 (см. таблицу). Однако, как показано на диаграмме (рис. 3а), её процессоры недогружены более чем наполовину.
Более эффективную структуру S3 можно получить, отобразив в одну вершину ПЭ пары соседних операторов алгоритма, имеющих одинаковую координату k. При этом можно достичь почти предельной загруженности ПЭ полученной вычислительной схемы C3 . Но выражение загруженности, представленное в таблице, не учитывает простоев ПЭ во время вычислений функций f1 и f2.
В современных ПЭ практически всегда существуют простои, связанные с моногоступенчатой обработкой данных. Во-первых, загрузка вычислительных модулей внутри ПЭ при вычислении функций f1 и f2 чаще всего несбалансирована. Эти вычислительные модули, например, умножитель, сумматор, обычно выполнены в виде конвейеров, которые имеют простои, если не организован непрерывный поток данных через них. Во-вторых, ПЭ соединены между собой каналами связи с конвейерной организацией и оборудование ПЭ простаивает, если не запрограммированы межпроцессорные пересылки на фоне вычислений. Рассмотрим подход, который позволяет снизить эти простои.
В вычислительной схеме C3 существуют относительно независимые параллельные ветви вычислений, которые сдвинуты во времени относительно друг друга, как например, ветвь, исполняющая операторы вершин с координатами (1, 9, 1), (1, 8, 1), (1, 7, 1),… и ветвь, исполняющая (2,9,2), (2,8,2), (2,7,2),… . Вычисление этих ветвей можно совместить в одном ПЭ, если организовать в нем конвейерный режим вычислений.
Пусть при вычислении функций f1 и f2 вычислительные модули в ПЭ загружены не более, чем на 1/QP. Тогда, руководствуясь методикой отображения алгоритмов в конвейерные вычислительные устройства [17, 18], можно организовать вычисление в ПЭ до QP операторов первого или второго типов в конвейерном режиме. Целый коэффициент QP в зависимости от сложности функций f1 и f2 , количества вычислительных модулей в ПЭ, числа ступеней их конвейеров, задержки межпроцессорных связей и может принимать значение от 2 до 5 и более.
Cтруктурa S4 при конвейерных вычислениях операторов получается путем объединения в одну вершину ПЭ QP вершин структуры S3, имеющих одинаковую координату j’ или склеиванием 2QP вершин первого типа и 2QВQP вершин второго типа в структуре S1 (на рис. 2 склеиваемые вершины обведены пунктиром). На рис. 3.б показана временная диаграмма загруженности полученной вычислительной схемы C4 при QP = 2.
Загруженность ПЭ схемы C4 такая же, что и у схемы C3. Но благодаря организации конвейерных вычислений в ПЭ, производительность ПЭ возрастает в QP раз и во столько же раз можно уменьшить число ПЭ в ПВС без заметного снижения ее производительности.
Для исследования особенностей отображения алгоритма Гивенса в вычислительную схему C4 и подтверждения её работоспособности были рассмотрены два примера её реализации. В первом примере алгоритм Гивенса был реализован в ПВС из сигнальных микропроцессоров с плавающей запятой серии Motorola DSP96000. Для извлечения квадратного корня с одинарной точностью при вычислениях с плавающей запятой функции f1 в микропроцессоре выполняются следующие вычисления:
p1 = p0 (3−q p0 p0); p2 = p1 (12−q p1 p1) /16,
где q = x2+y2; p2 = 1/√q; p0 – приближенное значение функции 1/√q, получаемое в микропроцессоре по специальной команде. Тогда результатами функции f1 являются: c = xp2; s = yp2 и b = qp2.
С помощью методики программной конвейеризации [19] этот алгоритм и алгоритм вычисления функции f2 были отображены в вычислительные схемы конвейеров, которые затем были реализованы в виде программных циклов микропроцессора. При этом f1 выполняется с циклом 18 тактов, а f2 – с циклом 6 тактов.
Таким образом, алгоритм Гивенса реализуется на двумерной матрице сигнальных микропроцессоров с параметрами QB = 3 и QP = 2, причем длительность такта вычислительной схемы равна 6 машинных тактов микропроцессора. Для матрицы размером 9*9 время вычисления алгоритма в процессорной матрице из М1∗М2 = 8 ПЭ составляет (2QB+QB/QP)n−3QB−1 = 61 такт или 366 тактов микропроцессора, не считая времени, необходимого на загрузку исходных данных, организацию циклов и т.п. Средняя загруженность такой ПВС по исполнению функций f1 и f2 равна 1/(3/QP+0,5/QP2) =0,57.
Данная вычислительная схема была запрограммирована в четырехпроцессорной ПВС [19]. При этом ПЭ программировались таким образом, чтобы последовательно
выполнять операторы РФГ, отображаемые в соответствующие ПЭ структуры S4, т.е. вершины ПЭ структуры скклеивались между собой с получением структуры данной ПВС. При этом достигалась почти предельная загруженность микропроцессоров ПВС.
В последнее время все шире применяются конфигурируемые ПВС, реализованные на базе программируемых логических интегральных схем (ПЛИС). Применение ПЛИС для решения задач линейной алгебры ограничено тем, что в них реализуется эффективно только лишь целочисленная арифметка, которая не обеспечивает необходимую точность вычислений. Алгоритм Гивенса характерен тем, что он более устойчив к погрешностям вычислений и поэтому он может быть реализован в ПЛИС. В [4,10] для реализации декомпозиции Гивенса предложено использовать алгоритмы “цифра за цифрой” , основанные на элементарных вращениях комплексного вектора. При этом функция f1 вычисляется за n итераций по формулам:
ξi = signyi ; xi+1=xi+ ξiyi2−i; yi+1=yi– ξiyi2−i;
ci+1= ci+ ξisi2−i; si+1= si− ξici2−i; i=0,…,n−1;
с начальными условиями: x0=|x|; y0=y; s0=0; c0= ky≈0,607; ξ = signx, и
результатами: b= ξ xnky; yn≈0; s=sn; c= ξcn. При этом пары xi,yi и ci,si представляют собой координаты комплексных векторов, которые после n элементарных вращений поворачиваются на угол arctg(y/x) и удлинняются в 1/ky раз.
Этот алгоритм и вычислительная схема С4 были реализованы в ПЛИС серии Xilinx Virtex [20]. Данные a,b были представлены 32−разрядными, а c,s − 17−разрядными целыми числами. Функция f1 вычислялась на 16−уровневом конвейере, а фунция f2 − на комплексном умножителе с тремя ступенями конвейера. При этом ПЭ первого типа имеет аппаратные затраты 670 эквивалентных конфигурируемых логических блока (ЭКЛБ), а ПЭ второго типа − 710 ЭКЛБ. Шестипроцессорная ПВС была реализована в ПЛИС типа XCV800, которая имела тактовую частоту до 50 МГц. При обработке матриц с размерами 9*9 достигается эквивалентная производительность до 280 мегафлопс.
Производительность ПВС на ПЛИС пропорциональна количеству ПЭ, которое выбирается в зависимости от логической емкости ПЛИС. Например, для микросхемы XC2V6000, обладающей большими ресурсами аппаратных умножителей, оно достигает 48 ПЭ. В состав ПЛИС входят также десятки блоков памяти, которые при реализации режима вычислений с ограниченным параллелизмом обеспечивают обработку матриц больших размеров. Необходимая точность вычислений может быть получена увеличением разрядности данных до сотни и более бит. Реализация конвейерного режима вычислений с коэффициентом QP=2,…,16 обеспечивает почти полную загруженность ПЛИС при максимальной производительности ПВС.
В результате применения методов синтеза систолических процессоров и путем укрупнения графов структур и конвейеризации вычислений получена новая вычислительная схема C3 реализующая алгоритм Гивенса. При этом по сравнению со схемой Самеха−Кука, достигается в 1,5 раза большее максимальное ускорение вычислений, и в 3QВ раз большая загруженность процессорных элементов. По сравнению со схемой C3 в схеме C4 количество ПЭ уменьшено в QP раз при приблизительно такой же производительности, благодаря организации параллельной обработки до QP ветвей алгоритма в конвейерном режиме. Приведенные примеры ПВС, реализующих эту схему, подтверждают ее высокую эффективность.
С каждой из полученных вычислительных схем C1,…,C4 можно получить вычислительную схему с меньшими аппаратурными затратами и с пропорционально большим временем вычисленной путем отображения группы ПЭ схемы в один ПЭ реальной структуры с соответствующим замедлением вычислений. Поэтому схемы C3 и C4, в которых минимизированы аппаратурные затраты, имеют высокий потенциал при масштабировании задачи QR-разложения, т.е. широкие возможности варьирования числа процессоров и размера задачи. В них в максимальной степени использованы операционные ПЭ, выполненных на современной элементной базе, например, на суперскалярных микропроцессорах. Поэтому реализация этой схемы в современных мультипроцессорных ПВС может дать большой прирост производительности. Также эта схема оптимизирована для реализации в специализированных ПВС. Примеры реализации схемы C4 на базе сигнальных микропроцессоров с плавающей запятой и ПЛИС это подтверждают.
Таблица
| Вычис- литель- ная схема |
Размеры ВС, М1 ∗ М2 |
Время вычислений, TB |
Ускорение, Ky |
Загруженность, η |
| С1 | (n−1) ∗ n | (3n−4)QB | n2/(9QB) | 1/(9QB) |
| С2 | (n−1)∗ (](n−1)/QB[+1) |
(2QB+1)n−3QB−1 | n2/(6QB+3) | 1/(6+3/QB) |
| С2 | ](n−1)/2[∗ (](n−1)/QB[+1) |
(2QB+1)n−3QB−1 | n2/(6QB+3) | 1/(3+1,5/QB) |
| С4 | ](n−1)/(2QP)[∗ (](n−1)/QB[+1) |
(2QB+QB/QP)n− 3QB−1 |
n2/(3QB(2+1/QP)) | 1/(3+1,5/QB) |
ЛИТЕРАТУРА
1. Выжиковски Р., Каневский Ю.С., Масленников О.В. Отображение алгоритма исключения Гаусса с частичным выбором ведущего элемента //Электронное моделирование.-1991.-13, № 2.-С. 14-20.
2. Ортега Дж. Введение в параллельные и векторные методы решения линейных систем.-М.: Мир, 1991.-366 с.
3. Golub G.H., Vam Loan C.F. Matrix computations.-Baltimore, London: John Hopkins University Press.-1989.-p. 642.
4. Gjotze J. and Schwiegelsohn V. A square root and division free Givens rotation for solving least square problems on systolic arrays // SIAM J. Sci. Statist. Comput.-1991.-V. 12.-N 4,p. 300-807.
5. Valero-Garcia M., Navarro J.J., Llaberia J.M., Valero M. and Lang T. A method for implementation of one- dimensional systolic algorithms with data contraflow using pipelined functional units. J. of VLSI Signal Processing, -V. 4, -1992, p. 7-25.
6. Heller D.H., Ipsen I.C.F. Systolic Networks for Orthogonal Equivalence Transformations and their Application //Conf. on Advanced Research in VLSI. Cambridge. MA; M.I.T. Press,-1982.-p. 113-122.
7. Ahmed H.M., Desolme J.M. and Morf M. Higly Concurrent computing structures for matrix arithmetic and signal processing //Computer,-1982.-V. 15.-p. 65-82.
8. Bojanczyk A., Brent R.P., Kung H.T. Numerically stable solution for dense systems of linear eguations using mesh-connected processors //SIAM J. Sci Statist. Comput.-1984.-V. 1,-p. 95-104.
9. Gentleman W.M., Kung H.T. Matrix triangularization by systolic arrays //Proc. SPIE,Real-Time Signal Processing IV.-1981.-p. 19-26.
10. Luk F.T. A rotation method for computing the QR-decomposition, SIAM J. Sci. Statist. Comput.-1986.-V. 7.-p. 452-459.
11. Schwiegelsohn V. and Thide. One- and two-dimensional arrays for least sguares problems// Proc. Int. Conf. on Acoust., Speech and Signal Processing,Dallas, T.X.-1987.-p. 791-794.
12. Chun J., Kailath T., Lev-Ari H. Fast parallel algorithms for QR and triangular factorization //SIAM J. Sci. Statist. Comput.-1987.-V. 6, p-899-913.
13. Каневский Ю.С. Систолические процессоры.-Киев: Технiка. 1991.-173 с.
14. Системы параллельной обработки/ под ред. Д. Ивенса.-М.: Мир. 1985.-414 с.
15. Рао С.Ю., Кайлат Е. Регулярные итерационные алгоритмы и их реализация в процессорных матрицах //ТИИЭР,-т. 76.- № 3, 1988.-с. 58-69.
16. Каневский Ю.С., Логинова Л.М., Сергиенко А.М. Структурное проектирование рекурсивных цифровых фильтров //Электронное моделирование. 1995, № 3, с. 18-22.
17. Каневский Ю.С., Сергиенко А.М. Формализованное проектирование систолических структур и их процессорных элементов //Автоматика и вычислительная техника. -1990,-№ 3.-с. 72-78.
18. Каневский Ю.С., Овраменко С.Г., Сергиенко А.М. Отображение регулярных алгоритмов в структуры специализированных процессоров // Электрон. Моделирование. -Т.24. -№2.-с.46-59.
19. Sergyienko A., Kaniewski J., Maslennikov O., Wyrzykowski R. Mapping regular algorithms into processor arrays using software pipelining. // Proceedings of the 1-st Int. Conf. on Parallel Computing in Electrical Engineering. PARELEC’98. Bialystok, Poland. – 2-5 Sept., -1998. -P.197-200.
20. Sergyienko A., Maslennikov O.. Implementation of Givens QR Decomposition in FPGA. Lecture Notes in Computer Science, Springer, 2002, Vol.2328, pp. 453-459.