Отображение регулярных алгоритмов в структуры специализированных процессоров

⇓Загрузить PDF (рус.)

Электрон. моделирование.-2002. —Т.24. —№2. —С. 46-59.

Ю.С. Каневский, д-р техн. наук, C.Г. Овраменко, А.М. Сергиенко, канд. техн. наук
(Национальный технический университет Украины “КПИ”)

Отображение регулярных алгоритмов в структуры специализированных параллельных процессоров
(Статью представил д-р техн.наук В.П.Симоненко)

Рассмотрен метод отображения алгоритма, представленного гнездом циклов в структуру специализированного параллельного процессора. Метод заключается в размещении редуцированного графа зависимостей алгоритма в многомерном индексном пространстве и отображении его в подпространства структур и времени. Предложенные ограничения на временную и пространственную компоненты отображения позволяют получить структуру с конвейеризованными процессорными модулями и упростить процесс отображения.

Розглянуто метод відображения алгоритма, який представлено гніздом циклів, в структуру спеціалізованого паралельного процесора. Метод полягає в розміщенні редукованого графа залежностей алгоритма в багатовимірному індексному просторі і відображенні його у підпростори структур і часу. Запропоновані обмеження на часову і просторову компоненти відображення дозволяють отримати структуру з конвейеризованими процесорними модулями і спростити процес відображення.
К л ю ч е в ы е с л о в а : граф алгоритма, гнездо циклов, конвейерные вычисления, отображение алгоритма, цифровая обработка сигналов.

Автоматическая разработка специализированных параллельных процессоров, например для цифровой обработки сигналов (ЦОС), сокращает путь проекта от идеи до рынка и затраты на их проектирование. Использование программируемых микросхем, таких как программируемые логические интегральные схемы (ПЛИС) позволяет вести разработку опытных образцов этих устройств с минимальными временными и финансовыми затратами.

Однако сейчас программирование ПЛИС выполняется, в основном, вручную с использованием языка описания функциональных схем, например VHDL, и требует высокой квалификации разработчика [1]. Поэтому большое значение имеет разработка програмных средств для автоматизации отображения регулярных алгоритмов, какими являются алгоритмы ЦОС, в функциональные схемы, адаптированные к структуре ПЛИС.

Алгоритмы ЦОС, как правило, выполняются в реальном времени над потоком данных и поэтому имеют итерационный характер. Рассмотрим алгоритмы, которые можно представить регулярными гнездами циклов или регулярными рекуррентными уравнениями. Ядро регулярного гнезда циклов стоит из одного или несколько операторов вида

St_i: a[I] = f(a[I+D₁], b[I+D₂],…),

где I – вектор индексов переменных a, b,…, равный вектору, принадлежащему n -мерному итерационному пространству Zⁿ, D_j – вектор приращений индексов j – й переменной, характеризующей зависимость по данным между итерациями I и (I+D_j).

Если ядро циклов содержит один оператор St или несколько операторов St_i которые могут быть сведены к одному оператору, то в таком алгоритме отсутствуют циклы зависимости между итерациями. Тогда все вычисления, выполняемые в одной итерации, могут быть спланированы так, чтобы начинаться в одно время [2]. Разработаны методы отображения таких алгоритмов в структуры систолических процессоров (см., например, [2 – 4]). Эти методы основаны на аффинном преобразовании с матрицей P итерационного пространства Zⁿ в подпространство структур Z^m и времени Z^n-m, таком, что оператор St_i, из I-й итерации вычисляется в процессорном элементе с координатами K_S = P_S I , K_S ∈ Z^m в момент времени, обозначенный K_T = P_T I, K_T ∈ Z^n-m, P = (P_S^Т,P_T^Т)^Т. Рассмотрим случай отображения, когда n – m = 1. Это отображение корректно при выполнении условия монотонности D_jP_T ≥ 0 и условия инъективности det P ≠ 0 .

Если в алгоритме существуют циклы зависимостей между итерациями, то отображение такого алгоритма выполнять сложнее [2]. Известны методы отображения этих алгоритмов основанные на отображении каждого оператора St_i ядра циклов с помощью отдельного аффинного преобразования [5, 6]. В этом случае поиск отображения алгоритма решается как задача целочисленного линейного программирования с ограничениями на эти аффинные преобразования и с учетом монотонности зависимостей между всеми переменными. Применение этого метода дает точное оптимальное решение, но для алгоритма с несколькими десятками операторов St_i решение невозможно найти за приемлемый промежуток времени [6].

Указанные методы имеют ряд ограничений. Прежде всего, предполагается, что операторы St_i, относящиеся к одной итерации, должны начинаться одновременно и выполняться в течение одного такта. Следовательно, хотя систолический процессор и представляет собой многомерную конвейерную систему, отдельные, часто сложные операторы не могут быть выполнены в конвейерном режиме. Другим ограничением является то, что в результате отображения получают структуру с максимальной пропускной способностью, а не с заданной.

Применение конвейеризованных процессорных элементов (ПЭ) позволяет повысить пропускную способность процессора ЦОС, благодаря возможности начать вычисление нового оператора прежде, чем завершится вычисление предыдущего. Поэтому разработка конвейеризованных ПЭ привлекательна с точки зрения аппаратурной реализации любых алгоритмов, в том числе алгоритмов ЦОС. В работе [7] предложен метод проектирования систолических процессоров с конвейеризованными ПЭ. Однако этот метод не является конструктивным, так как заключается в ручном введении ступеней конвейера в готовую схему систолического процессора.

В данной статье предлагается новый метод проектирования специализированных параллельных процессоров путем отображения алгоритмов, заданных регулярными циклами, в их структуры, позволяющий формализованно проектировать параллельные системы ЦОС с заданной пропускной способностью и с конвейеризованными ПЭ.

Исходные данные и цели проектирования процессоров ЦОС. Предлагаемый метод представляет собой доработанные известные методы синтеза систолических процессоров. Целью доработки методов является следующее:

1) Вычисления операторов за время, превышающее один такт. Это позволяет получить параллельный процессор с заданной пропускной способностью и реализовать операторы St_i алгоритма с произвольной сложностью (причем разные операторы могут иметь различную сложность, допускаются циклы зависимости по данным между итерациями). В результате расширяется область реализуемых алгоритмов, различные операторы St_i ядра циклов могут иметь различные моменты начала выполнения.

2) Конвейеризация вычислительных модулей процессорных элементов. Несмотря на то, что латентная задержка ПЭ становится большей, пропускная способность процессора увеличивается за счет конвейеризации, благодаря которой повышается максимальная тактовая частота.

3) Использование одних и тех же процессорных модулей для реализации различных операторов алгоритма, а также специализированных модулей, что позволит эффективнее загрузить оборудование процессора.

Рассмотрим алгоритм, заданный единичным циклом:

for i = 1, Ui do
 (y1[i]),...,yp[i])=f(y1[i+di1],...,yq[i+diq]);
end

         (1)

Функция f вычисляется по алгоритму, состоящему из U_j унарных и бинарных операторов присваивания St_j. Следовательно, алгоритм (1) можно представить так:

for i = 1, Ui do
    {оператор St1}
    . . .
  Stj: y[i, j] = ϕj,k(y[i-di1, j], y[i-di2, j])
    . . .
    {оператор StUj}
end

         (2)

где ϕ_j,k(x,y) – оператор k – го типа, выполняемый над операндами x,y. Данный цикл можно преобразовать в трехуровневое гнездо циклов, такое, что в (i, j, k)-й итерации выполняется только j-й оператор и только k-го типа или никакой другой оператор.

for i = 1,Ui do
  for j = 1,Uj do
    for k = 1,Uk do 
    if (j,k) ∈ Φ then y[i,j] = ϕj,i(y[i-di1, j], y[i-di2, j]);
    end;
  end;
end

         (3)

где Φ – множество допустимых пар (j,k), определяющих тип и очередность выполнения операторов в алгоритмах (2) и (3).

Таким образом, цикл (1) с ядром из нескольких разнотипных операторов можно представить гнездом из трех циклов (3), вычисления которого происходят в области вычислений K³ трехмерного итерационного пространства Z³, {K³ = (1≤ i≤ U_i; 1≤ j≤ U_j, 1≤ k≤ U_k)} ⊂ Z³. Аналогичным образом можно представить гнездо циклов большей размерности. Каждому оператору алгоритма соответствует трехмерный вектор K_i ∈ K³ , а зависимости по данным между i -м и l -м операторами соответствует вектор зависимости D_j = K_i – K_l. В большинстве случаев вектору D_j соответствует переменная – результат оператора, обозначенного K_i, но передаваемая различным операторам, обозначенным K_l, в качестве входной переменной.

В указанных методах синтеза структур специализированых вычислительных систем предполагается отображать операторы St_j в универсальные ПЭ или ПЭ, выполняющие заданный набор операций. Рассмотрим применение специализированных ПЭ, выполняющих по одной функции ϕ_k. Базовый набор таких ПЭ для реализации задач ЦОС может включать элементарные ПЭ типа сумматор, умножитель, ПЗУ и других, локальная память которых организована в виде стека FIFO или одного регистра результата функции ϕ_k.

Отображение регулярных циклов в структуру специализированного параллельного процессора. В методах, описанных в [2 – 6] граф G_A алгоритма размещается в n-мерном индексном пространстве Zⁿ. Так как граф G_A в систолических алгоритмах является регулярным решетчатым графом, он представляется компактно в виде множества неповторяющихся векторов-дуг D_j информационных зависимостей. В случае, когда ядро цикла алгоритма состоит из нескольких операторов, такое, как в алгоритме (2), то компактной формой алгоритма является редуцированный граф G_AR информационных зависимостей. В этом ориентированном графе N вершин-операторов K_i связаны M векторами-дугами D_j информационных зависимостей.

Рассмотрим алгоритм:

for i = 1, N do
  for j = 1, M do
    St1: a[i,j] = b[i-1, j-1];
    St2: b[i,j] = a[i,j];
  end;
end

Этому алгоритму соответствует редуцированный граф зависимостей (рис. 1.). Цикл графа показывает цикл межитерационной зависимости алгоритма. Векторы-дуги D₁ и D₂ соответствуют передаче между операторами St₁ и St₂ переменных a и b и нагружены величиной относительной задержки передачи данных (0, 0) и (1, 1).

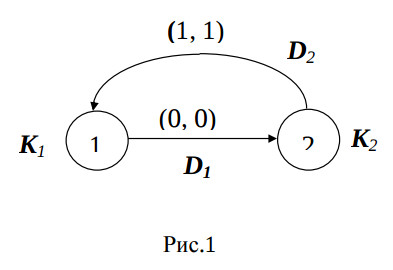
Для задания редуцированного графа G_AR зависимостей в n-мерном пространстве необходимо, кроме матрицы D векторов D_j информационной связи, иметь матрицу K векторов K_i координат вершин операторов, а также матрицу A инцидентности этого графа размерностью (M+1)N. Тогда матрицы K, D и A образуют конфигурацию алгоритма C_A. Следующие определения и зависимости истинны для конфигураций C_A. Конфигурация C_A корректна, если K_i ≠ K_j, i, j = 1,…,N, i ≠ j, т.е. если все векторы-вершины разделены в пространстве Zⁿ. Существует линейная зависимость между матрицами конфигураций, т. е.

D = KA;     K = D₀A₀^-1,       (4)

где A₀ – матрица инцидентности для остова графа G_AR , а D₀ – матрица векторов-дуг этого остова. Например, для графа, приведенного на рис. 1, справедливо следующее:

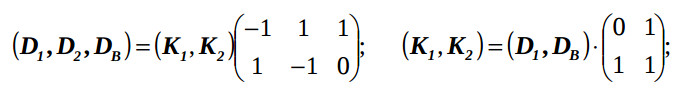
где D_B – базисная вектор-дуга, соединяющая вектор-вершину K₁ с началом системы координат.

Сумма векторов-дуг D_j, входящих в любой из циклов графа G_AR, должна быть равна нулю, т.е. для i-го цикла

где b_i,j – элемент i-й строки цикломатической матрицы графа G_AR.

Конфигурации C_A¹ = (K₁,D₁,A₁) и C_A² = (K₂,D₂,A₂) эквивалентны, если они корректны и представляют один и тот же граф, т.е. A₁ = A₂.

Корректная конфигурации C_A¹ эквивалентна конфигурации C_A², если A₁ = A₂ и K₂ = F(K₁), где F — инъективная функция. Например, перестановка векторов K_i в пространстве Zⁿ, эквивалентная перестановке строк или столбцов матрицы K₁, умножение матрицы K₁ и невырожденной матрицы P.

Граф G_S структуры процессора можно представить с помощью конфигурации G_S = (K_S, D_S, A), где K_S – матрица векторов-вершин K_Si ∈ Z^m, которые равны координатам ПЭ, а D_S – матрица векторов дуг D_Sj ∈ Z^m, представляющих соединения между ПЭ.

Наконец, конфигурация предшествования C_T = (K_T, D_T, A) состоит из матрицы K_T векторов K_Ti ∈ Z^{n – m}, матрицы D_T векторов D_Tj и матрицы A. Здесь векторы K_Ti представляют моменты выполнения операторов алгоритма. В корректной конфигурации C_T вектор-дуга D_Tj=K_Tl–K_Ti означает, что оператор вершины K_Ti должен предшествовать во времени оператору вершины K_Tl.

Временная функция R(K_Ti)= t_i выполняет отображение пространства Z^{n – m}событий на ось времени и определяет истинный момент выполнения оператора. Конфигурация C_T корректна или, другими словами, условие предшествования отображения истинно, если для любой пары векторов-вершин K_Ti и K_Tl выполняется неравенство R(K_Tl)>R(K_Ti), где i-й оператор предшествует l-му оператору.

Допустим, что функция R линейная и монотонная, то конфигурация C_T корректна, если D_Tj ≥ 0, j=1,…,M, где D_Tj представляют временные компоненты векторов непосредственной информационной зависимости, которые отвечают ненагруженным (или нагруженным нулем) дугам редуцированного графа G_AR зависимостей, ≥ — знак лексикографического неравенства. Функция R(D_Tj) равна задержке между моментом, когда j-я переменная начинает вычисление, и моментом, когда она поступает в другой ПЭ. Эта задержка определяет верхнюю границу объема ОЗУ, в котором хранится j-я переменная.

Рассмотрим метод поиска пространственной и временной компонент отображения алгоритма вида (2) в структуру специализированного процессора, который вычисляет ядро цикла с периодом τ тактов. Данный метод можно обобщить на случай отображения многоуровневого гнезда циклов.

Как показано выше, алгоритм (2) можно представить в трехмерном индексном пространстве, в котором векторы-вершины K будут иметь координаты (j, k, i)^T, где i означает номер цикла, j — номер оператора и k — тип оператора. Аналогично можно добавить еще одну размерность – номер такта q в цикле, тогда вектор K = (j, k, i, q)^T. Этот алгоритм можно представить в виде редуцированного графа зависимостей G_AR и в виде конфигурации алгоритма C_A. Также следует выполнить кодировку веса векторов-дуг D_j. Значение p < 0 координаты номера цикла и нулевое значение номера такта вектора D_j означает, что соответствующая дуга имеет вес, равный p.

Конфигурация алгоритма C_A представляет собой композицию конфигураций структуры C_S и предшествования C_T, так что K = (K_S^T, K_S^T)^T и если K_l = (j, k, i, q)^T, то K_Sl = (j, k)^T и K_Tl = (i, q)^T.

Сначала выполняетя поиск пространственной компоненты отображения матриц K_S и D_S. В векторе K_Sl = (j, k)^T координата j равна номеру ПЭ, в котором выполняется l-й оператор, а k — типу этого оператора. Формирование матрицы K_S искомой конфигурации структуры — это комбинаторная задача. При этом M_k операторов k-го типа распределяется среди не менее чем ]M_k/τ[ процессорных элементов также k-го типа. Таким образом, в матрице K_S формируются M_S груп одинаковых столбцов, в каждой из которых не более τ столбцов, где M_S — число ПЭ в результирующей структуре. При этом достигается максимальная загруженность j-го ПЭ, если число столбцов в матрице K_S с j-м элементом равно τ. Матрица D_S находится из выражения: D_S = K_SA.

Временная компонента отображения в виде матриц K_T и D_T определяется, исходя из соблюдения условий корректности конфигурации алгоритма, конфигурации предшествования и равенства нулю сумм векторов-дуг, входящих в циклы графа G_AR. Кроме того, заданный алгоритм будет выполняться правильно тогда и только тогда, когда соответствующие конфигурации алгоритма C_A и предшествования C_T корректны и

∀K_T ∈ K_T(K_T = (i, q)^T, i ≥ 0, q ∈ (0, 1,…,τ-1)).

Стратегию поиска пространственной и временной компонент отображения можно проследить на примере синтеза структуры специализированного процессора.

Пример синтеза структуры рекурсивного фильтра. Рассмотрим синтез структуры рекурсивного фильтра, который вычисляется по формуле y[i] = x[i]+ay[i-2]+by[i-1]. Этой формуле соответствует следующий алгоритм

for i = 1, N do
 St1: y1[i] = a*y[i-2];       St2: y2[i] = b*y[i-1];
 St3: y3[i] = x[i]+y1[i];       St4: y[i] = y2[i]+y3[i];
end.

Редуцированный граф зависимостей для этого цикла приведен на рис. 2.

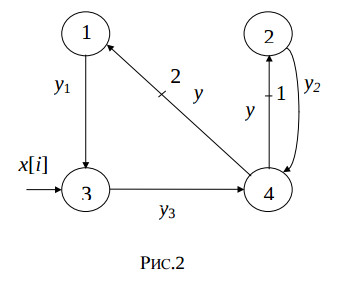
Каждый из операторов St₁,…,St₄ должен выполнять действие не менее чем за один такт. Нагруженные дуги, выходящие из третьей и четвертой вершины, выражают задержку переменной y[i] на один и два цикла и не могут выразить задержку выполнения оператора St₄. Поэтому, в эти дуги вставляются промежуточные вершины, выполняющие функцию повторения. Модифицированный редуцированный граф зависимостей показан на рис. 3.

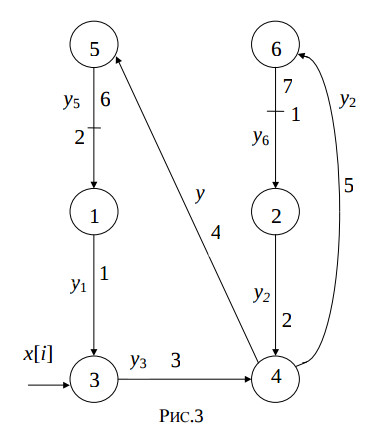
Этому графу соответствует следующий алгоритм:

for i = 1, N do
 St1: y1[i] = a*y5[i-2];      St2: y2[i] = b*y6[i-1];
 St3: y3[i] = x[i]+y1[i];      St4: y[i] = y2[i]+y3[1];
 St5: y5[i] = y[i-2];      St6: y6[i] = y[i];
end.

Поскольку в алгоритме по два оператора сложения и умножения, целесообразно выполнить фильтр на одном умножителе и одном сумматоре и выбрать период выполнения алгоритма τ = 2.

Определим пространственную компоненту отображения в виде матриц K_S и D_S. При этом в матрицу K_S подставляются допустимые значения координат векторов вершин K_Si : K_S=((1,1)^Т(1,1)^Т(2,2)^Т(2,2)^Т(3,0)^Т(3,0)^Т).

Здесь значения координаты k = 0, 1, 2 представляют операторы соответственно умножения, сложения, тождественности, а одинаковые значения координаты j означают, что операторы будут выполняться в одном и том же ПЭ. Матрицу D_S относительных координат линий межпроцессорных
связей получим из выражения:

Вычислим временную компоненту отображения. Прежде всего определим известные координаты векторов. Это взвешенные векторы информационной зависимости D_T6=(-2,0)^T и D_T7=(-1,0)^T.

Исходя из периода τ = 2 вычисления алгоритма, определим временную функцию R = (τ,1) = (2,1). Для того чтобы число регистров в ПЭ умножителя и сумматора было минимальным, векторы зависимости D_Tj, выходящие из вершин 1,…,4 должны принимать такие значения, что RD_Tj ∈{1,2}, т.е. (0,1)^Т, (1,-1)^Т и (1,0)^Т, а это также удовлетворяет условию монотонности отображения.

Для выполнения условия инъективности отображения различными должны быть значения координаты q векторов K_T с одинаковыми координатами j, вектор K_T1 должен быть равен (X,0)^T или (X,1)^T, а вектор K_T2 равен (X,1)^T или (X, 0)^T. Здесь X — неизвестная пока величина.

Соответствующие координаты q векторов относительной задержки D_T находятся из уравнения D_T = K_T A. Координаты векторов относительной задержки также должны отвечать условию равенства нулю суммы векторов входящих в цикл:

D_T1+D_T3+D_T4+D_T6 = 0;       D_T2+D_T5+D_T4+D_T6 = 0.

Исходя из этих условий находится единственное решение:

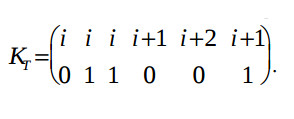
На рис. 4 а – г, показаны результаты проектирования соответственно: редуцированный граф зависимостей в пространстве времени-места, граф структуры, структура фильтра и граф алгоритма ее работы. Приведенная на рисунке структура отличается максимальной загруженностью ПЭ и работой в конвейерном режиме. При этом минимальная длительность тактового интервала равна задержке одного умножителя.

Возможные пути реализации метода. Отображение алгоритма в структуру специализированного вычислителя предлагаемым методом представляет собой комбинацию задач планирования вычислений и их назначения на ресурсы, т.е. является NP- полной задачей. Реализовать метод можно, используя один из нескольких методов решения сложных задач. Сложность задачи заключается в трудоемкости поиска оптимального решения в пространстве возможных решений. В соответствии с предлагаемым методом каждое решение можно закодировать матрицей K. Необходимые ограничения, накладываемые на конфигурацию алгоритма, а следовательно и на матрицу K, на несколько порядков сокращают пространство возможных эффективных решений (уменьшают трудоемкость поиска оптимального решения).

Если размерность задачи невелика, когда число вершин редуцированного графа зависимостей не превосходит двух десятков, то поиск оптимального решения можно вести методом сканирования пространства возможных решений. Приведенный пример показывает, что при шести вершинах графа мощность пространства решений может уменьшиться с p²⁴ до единицы, где p — диапазон изменения элементов матрицы K. С помощью метода ветвей и границ можно получать оптимальное решение для графов с вдвое большим числом вершин, чем при применении метода сканирования.

Методы конструирования решения, такие как “жадный” алгоритм, позволяют получить оптимизированные решения за число шагов, пропорциональное числу вершин. Например, можно применить метод пошагового конструирования, при котором на i-м шаге находятся координаты вершин, выполняемых в i-м такте, таким образом, чтобы оценка сложности результирующей структуры была минимальной. Эффективные решения могут быть получены при использовании “жадного” алгоритма метода левого края (left edge shedule) [8].

В последнее десятилетие получили широкое распространение эволюционные методы оптимизации, такие как моделируемый отжиг (simulating annealing), совмещающий метод пошагового конструирования решения со случайным поиском и генетический метод [9]. Сложность разработки генетического метода заключается в поиске эффективного способа кодирования хромосомы, которой соответствует некоторое решение задачи проектирования, а также процедур скрещивания и мутации, обеспечивающих направленно-случайный поиск оптимизированных решений. В этом случае матрица K успешно выполняет функции хромосомы, а перестановка векторов между конфигурациями алгоритма и изменение их координат являются процедурами скрещивания и мутации.

Экспериментальные результаты. Предложенный метод отображения регулярных циклов был реализован в программном комплексе Parlab. В функции комплекса входит ввод, редактирование алгоритма, его графическое представление и отображение в структурную схему специализированного параллельного процессора. При отображении алгоритма оптимизируется загруженность процессорных элементов по приведенной стратегии. Оптимизация по методу левого края может выполняться автоматически. Кроме того, минимизируется общее число регистров в результирующей структуре, число входов мультиплексоров процессорных элементов и общее число линий связи. Комплекс Parlab реализован в среде Windows.

В качестве более сложного примера отображения выбрано отображение волнового эллиптического фильтра пятого порядка [10], который считается тестовым для систем автоматизированного отображения алгоритмов в вычислительную схему. Так, на этом примере показана эффективность программных комплексов SPAID и HAL [11]. В результирующей структуре предполагается, что умножение выполняется за два такта в конвейерном умножителе, а сложение за один такт. В таблице приведены данные об аппаратурных затратах для двух вариантов решения задачи проектирования схемы волнового эллиптического фильтра, отличающихся заданным периодом вычислений, с помощью указанных программных комплексов. Из таблицы видно, что с помощью комплекса Parlab получаются решения с меньшими аппаратурными затратами, измеренными в числе сумматоров, регистров и особенно, умножителей.

Результаты работы программного пакета Parlab можно использовать для программирования ПЛИС. Пакет был использован при проектировании для ПЛИС, выпускаемых фирмой Xilinx, вычислительных модулей рекурсивных и трансверсальных цифровых фильтров, процессоров быстрого преобразования Фурье и дискретного косинусного преобразования. Спроектированные модули отличаются от аналогичных модулей, предлагаемых в известном пакете Xilinx Coregen, более высоким отношением производительность-аппаратные затраты, возможностью настройки в большом диапазоне ряда параметров, таких как разрядность данных, длина фильтра, длина преобразования, серия ПЛИС. Пакет Parlab находится в доработке, в частности, разрабатываются программы графического представления структуры, описания реализующей структуры на языке VHDL для прямой стыковки со средствами программирования ПЛИС, программы автоматической оптимизации методами пошагового
конструирования, моделируемого отжига и генетическим методом.

Таким образом, описанный метод отображения алгоритмов, представленных гнездом циклов, является развитием метода, предложенного авторами в работах [12 – 14]. Метод предназначен для синтеза специализированных параллельных процессоров, работающих в конвейерном режиме с высокой производительностью, которая достигается за счет высокой загруженности ПЭ. Он состоит из матрично-графовых форм представления исходного алгоритма и результирующих вычислительных схем, называемых конфигурациями алгоритма, структуры и предшествования, а также способов их эквивалентных преобразований и направленного поиска оптимизированных решений. Преимущество метода заключается в том, что на его основе можно построить новые, более эффективные системы синтеза конвейеризованных вычислительных схем, используя известные методы решения сложных задач, такие, как методы конструирования решений, генетические алгоритмы и др.

Предложенный метод реализован в программном комплексе Parlab, применение которого позволяет автоматизировать проектирование специализированных процессоров для цифровой обработки сигналов и решения других задач. Синтезированные структурные решения могут быть эффективно реализованы на базе технологии ПЛИС.

Программный комплекс	Parlab	SPAID	HAL
Период вычислений τ,тактов	17    19	17    19	17    19
Умножителей, штук	1     1	2     2	2     1
Сумматоров, штук	3     2	3     2	3     2
Входов мультиплексоров, штук	41    43	35    24	37    28
Регистров, штук	11    10	21    21	12    12

1. Isoaho J., Pasanen J., Vainio O. DSP Sytem Integration and Prototyping With FPGAs // J. of VLSI Signal Processing. -1993, -6. -P. 155-172.

2. Рао С.K., Kайлат T. Регулярные итеративные алгоритмы и их реализация в процессорных матрицах // ТИИЭР. –1988.-76, -№ 3, – C. 58-69.

3. Молдован Д.И. Разработка алгоритмов для СБИС систолических процессоров // Там жеИИЭР. -1983.-71, -№ 1. -C. 140-149.

4. Кун С. Матричные процессоры на СБИС. -М.: Мир, -1991. -248с.

5. Quinton P. and Robert Y. Systolic algoritms and architectures. -Englewood Cliffs: Prentice Hall , -1991. – 360 p.

6. Darte A., Robert Y. Mapping uniform loop nests onto distributed memory architectures // Parallel Computing. -1994. –20. -P. 679-710.

7. Valero-Garcia M., Navarro J.J., Llaberia J.M., Valero M. and Lang T. A method for implementation of one- dimensional syStolic algorithms with data
contraflow using pipelined functional units // J. of VLSI Signal Processing. -1992.-4. -P. 7-25.

8. The Synthesis Approach to Digital System Design./ P.Michel, U.Lauther, P.Duzy, -eds. -Kluwer. -1993. –416 p.15

9. Chen H., Flann N.S., Watson D.W. Parallel Genetic Simulating Annealing: A massively Parallel SIMD Algorithm// IEEE Trans. Parallel and Distributed Systems.-1998. –9, -N2. -P.126-136.

10. Cверхбольшие интегральные схемы и современная обработка сигналов / Под ред. С. Гуна, Х. Уайтхауса, Т. Кайлата. -М.: -Радио и связь. -1989. –472 с.

11. Haroun B.S., Elmasry M.I. SPAID: An Architectural Synthesis Tool for DSP Custom Applications.// Proc. IEEE Custom Integrated Circuits Conf. Rochester,
N.Y. -May 16-19, -1988.- P.188-195.

12. Kanevski, J.S., Sergyienko, A.M., Piech H. A method for the Structural synthesis of pipelined array processors // 1-st Int. Conf. ‹‹Parallel Processing and Applied Mathematics››, PPAM’94, Czestochowa (Poland). -Sept. 14-16. -1994. – P. 100-109.

13. Kanevski, J.S., Sergyienko, A.M. Mapping numerical algorithms into multipipelined processors // Proc. Int. Workshop ‹‹Parallel Numerics’94››,Smolenice
(Slovakia). –1994. -P.192-202.

14. Каневский Ю.С., Логинова Л.М. , Сергиенко А.М. Cтруктурное проектирование рекурсивных цифровых фильтров // Электрон. моделирование.- 1995. -№ 3. -C.18-22.

⇓Загрузить PDF (рус.)