Спецпроцессоры для авторегрессионного анализа сигналов
к.т.н. А.М.Сергиенко, В.Л.Лепеха, Нац.техн.ун-т Украины «КПИ»
(37, пр. Победы, 03056, Киев, Украина
Teл.: (044) 4549337, Е-mail: aser@comsys.kpi.ua )
д.т.н. О.В.Масленников, Кошалинский политехн. ин-т
(Sniadeckich 2, 75 – 453 Koszalin, Poland.
E-mail: oleg@ie.tu.koszalin.pl)
Спецпроцессоры для авторегрессионного анализа сигналов
Авторегрессионный (АР) анализ – это эффективный способ для определения характеристик сложных физических объектов с дальнейшим их моделированием. Поэтому АР анализ прочно вошел в практику экономических расчетов, сейсморазведки, медицинской диагностики, мобильной связи, моделирования музыкальных инструментов.
Применение программируемых логических интегральных схем (ПЛИС) дает возможность анализировать сигналы в диапазоне частот до сотен мегагерц. Но при этом алгоритмы анализа должны использовать перимущественно арифметику с фиксированной запятой. В то же время, алгоритмы АР анализа требуют вычисления с повышеной точностью и часто выполняются с плавающей запятой. В докладе предлагаются структуры спецпроцессоров на базе ПЛИС, позволяющие выполнять АР анализ сигналов в широком диапазоне частот с применением целочисленной арифметики.
АР анализ основан на предположении, что исследуемый физический объект представим моделью АР-фильтра, выполняющего фильтрацию некоторого сигнала возбуждения, например, белого шума, с получением выходного дискретизованного сигнала x(n). Коэффициенты АР-фильтра – коэффициенты предсказания ai (i=0,…,p) находят в два этапа. Сперва вычисляют оценки автокорреляционной функции rxx(i), а затем решают нормальную систему уравнений Юла-Уолкера
Rxx (a1,…, ар)Т = – (rxx(1),…,rxx(p))Т, (1)
где Rxx – симметричная теплицева матрица с первой строкой rxx(1),…,rxx(p-1), а0=1 [1].
Систему уравнений чаще всего решают по алгоритму Дарбина, который можно описать следующим гнездом циклов
for i = 1 to p
a0 = 1;
ki = – (a0*ri +...+ai-1*ri)/Ei-1;
ai = ki;
for j = 1 to i-1
aj = aj + ki*ai-j;
end
Ei = (1-k2i)*Ei-1;
end;
(2)
где начальное значение ошибки предсказания E0 = r0. В качестве результатов анализа используют как коэффициенты предсказания ai, так и коэффициенты отражения ki. В практике АР анализа на основе коэффициентов ai выполняют спектральный анализ сигнала с высоким разрежением, а дистанцию между коэффициентами ki, приближающимся к 1 с различными знаками, трактуют как расстояние между слоями среды, в которой распространялся входной сигнал [1,7].
Как видим, алгоритм (2) требует порядка p2 операций и его трудно распараллелить. Поэтому часто рекомендуют вместо алгоритма Дарбина использовать более трудоемкие, но линейно распараллеливаемые алгоритмы, такие как алгоритмы QR-факторизации [2,3]. В этой связи алгоритм Гивенса или обращение теплицевой матрицы также может иметь преимущества при его реализации в ПЛИС [4,5].
Так как в (2) приходится делить на ошибку предсказания Ei, которая может стремиться к нулю, то для решения системы уравнений необходимы вычисления с повышенной точностью. Аналогичные свойства имеют и другие алгоритмы [2]. Поэтому чаще всего задачу АР анализа решают на микропроцессорах с плавающей запятой.
Для получения устойчивой оценки параметров ai необходимо накопить значения rxx(i) для не менее, чем qp =10р отсчетов данных [1]. При р, ограниченном десятками, сложность этапа вычисления корреляции приблизительно в р раз выше сложности решения системы уравнений. Если данные поступают последовательно, распараллеливание решения системы уравнений с применением многопроцессорной системы не даст заметного выигрыша в производительности, так как накопление корреляции будет превалировать в балансе времени. В этом случае предлагается процессор для АР анализа выполнить в виде блока коррелятора, состоящего из р процессорных элементов, работающих с фиксированной запятой и блока выполнения алгоритма Дарбина с арифметикой повышенной точности. При этом оба блока могут выполнять свои задачи приблизительно за одинаковое время.
В алгоритме (2) критический путь проходит через циклический участок получения коэффициента ki. При конвейерной реализации операций длительность итерации будет равна глубине конвейера сумматора. Если применять арифметические устройства с плавающей запятой, то длительность итерации будет равна не менее 7 тактов, т.е. блок будет простаивать большую часть времени [6].
В [5] предложено использовать для решения задач линейной алгебры арифметику рациональных дробей, которая может иметь преимущества перед плавающей запятой при своей реализации в ПЛИС. При этом число x представляется двумя целыми числами: числителем nx и знаменателем dx дроби, то есть x = nx/dx. Все вычисления алгоритма Дарбина предлагается выполнять с данными в виде таких дробей. При этом умножение, деление и сложение выглядит следующим образом:
x*y = nxny / (dxdy); x/y = nxdy / (dxny); x+y = (nxdy + nydx) / (dxdy).
Реализация такой арифметики в ПЛИС подерживается наличием большого количества блоков умножителей с аккумулятором, таких как DSP48 в ПЛИС серии Xilinx Virtex. При использовании этой арифметики для исполнения алгоритма Дарбина обеспечивается как малая погрешность вычислений, так и расширенный динамический диапазон в сравнении с арифметикой целых чисел, а также простота реализации в ПЛИС и высокое быстродействие. Кроме того, операция деления, входящая в цикл алгоритма, выполняется максимально кратко и с минимальной погрешностью. Если необходимо естественное представление результатов, то в конце вычислений числители дробей результатов ai или ki делятся на знаменатели обычным делением. При этом такое деление не увеличивает цикл работы процессора.
КИХ-фильтр с коэффициентами ai является обратным к АР-фильтру. Поэтому адаптивный КИХ-фильтр часто используют для получения коэффициентов авторегрессии [1,7]. Однако, медленная и не всегда надежная сходимость адаптации таких фильтров препятствует их применению для анализа быстропротекающих процессов.
Широко известна лестничная форма адаптивного КИХ-фильтра, j-я ступень которого выполняет вычисления [1]:
Efj(n) = Efj-1(n) + kjEbj-1(n-1); Ebj(n) = Ebj-1(n-1) + kjEfj-1(n),
где Efj(n), Ebj-1(n-1) –ошибки предсказания вперед и назад в n-м такте, соответственно, kj – коэффициент отражения, Ef0(n) = Eb0(n) = x(n), j=1,…,p. В фильтрах с последовательной адаптацией коэффициенты kj вычисляются по рекурсивному градиентному алгоритму. В фильтре для обработки блоков N = qp данных эти коэффициенты наиболее точно вычисляются по формуле [1]:
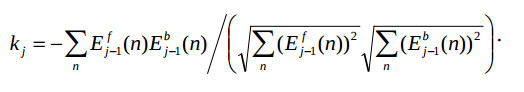
Здесь суммы в числителе и знаменателе являются оценками коэффициентов частичной корреляции. В такой вычислительной схеме коэффициенты kj находят последовательно, начиная с первого, р раз пропуская один и тот же массив данных через схему фильтра. Если сигнал стационарный в пределах pN отсчетов, то данные могут следовать непрерывно. Структура процессора для АР-анализа состоит из лестничного фильтра и блока вычисления коэффициентов kj. В процессе вычислений блок вычисления коэффициентов на j-м шаге адаптации подключается к входам j-й ступени фильтра, накапливает оценки коэффициентов частичной корреляции, вычисляет kj и подставляет его как множитель для умножителей j-й ступени фильтра. Таким образом, в данной схеме совмещены этапы накопления корреляции и вычисления коэффициентов отражения.
В отличие от традиционных схем адаптивных фильтров, здесь получается надежная сходимость адаптации за pN тактов. По сравнению со схемой, решающей
уравнения Юла-Уолкера, потенциально здесь нет накопления ошибок вычислений и всегда получаются стабильные результаты (т.е. когда |kj| < 1). Поэтому для реализации блока вычисления коэффициентов достаточно использовать арифметику целых чисел. Такой процессор АР анализа несложно реализовать в ПЛИС, хотя для этого необходима, по крайней мере, удвоенная разрядность при вычислении коэффициентов. Скорость схождения можно увеличить, поставив по блоку вычисления коэффициентов на каждую ступень фильтра, но тогда аппаратные затраты существенно возрастут.
Две вышеописанные вычислительные схемы для АР анализа были выполнены в виде спецпроцессоров, конфигурированных в ПЛИС фирмы Xilinx. Процессор, реализующий алгоритм Дарбина, имеет АЛУ, выполняющее параллельно операции умножения/деления, накопления в арифметике рациональных дробей с 18-разрядными числителем и знаменателем, а также преобразование дроби в целый 18-разрядный результат. Операции умножения/деления выполняются в конвейерном режиме с периодом 1 такт с латентной задержкой 7 тактов. Операция накопления выполняется за 4 такта, т.к. приходится ее результат использовать как исходное данное этой операции.
Результаты реализации процессоров для 16-разрядных данных, q = 10 и различных значений p представлены в табл.1. Их сравнение показывает, что процессоры с алгоритмом Дарбина имеют большую тактовую частоту, меньшие аппаратурные затраты и меньший цикл получения результатов (период адаптации). Анализ проектов показывает, что можно повысить частоту поступления входных данных вдвое, если тактировать блок вычисления корреляционной функции и лестничный
фильтр вдое большей частотой, чем блок вычисления коэффициентов.
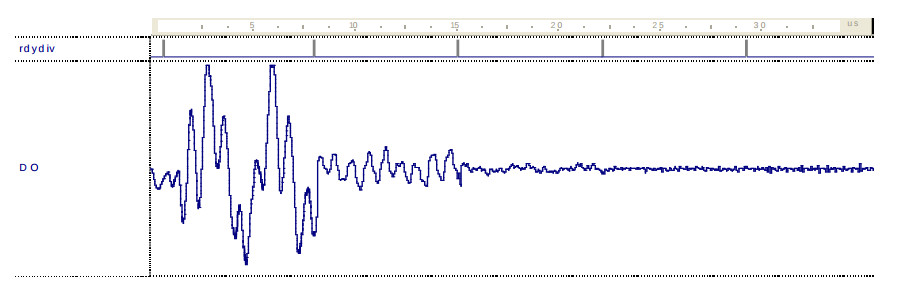
На рис.1 показан график ошибки предсказания лестничного фильтра при анализе белого шума, прошедшего через 3 ступени рекурсивных полосовых фильтров 2-го
порядка. Можно видеть быструю сходимость процесса адаптации после вычисления 4-5 коэффициентов kj (периоды вычисления отмечены импульсами). Таким образом, процессор на основе лестничного фильтра может иметь преимущество при р – малом и при q < 10, а также при обработке непрерывного потока данных. Кроме того, он обеспечивает устойчивую оценку kj для любых входных данных.
По сравнению с аналогичными проектами устройств для АР-анализа на базе ПЛИС [9,10] при сравнимой пропускной способности предлагаемые процессоры имеют существенно меньшие аппаратурные затраты. Так, при одинаковом числе блоков умножения (эквивалентных DSP48) фильтр [10] имеет почти в 20 раз большие аппаратурные затраты в количестве логических таблиц, чем процессор с алгоритмом Дарбина.
Taблица 1. Процессоры с порядком р, реализованные в ПЛИС XC4VSX35-12
| Процес- сор на основе | Аппарат. затраты, CLB slices + DSP48 | Макс. такт. частота, МГц | Длит-сть цикла получения k1 ,…, kр, тактов | ||||||
|---|---|---|---|---|---|---|---|---|---|
| р = 10 | р = 30 | р = 90 | р = 10 | р = 30 | р = 90 | р = 10 | р = 30 | р = 90 | |
| алго- ритма Дарбина |
1330 + 16 | 1850 + 36 | 4753 + 96 | 154 | 159 | 150 | 610 | 1830 | 5490 |
| лест- ничного фильтра |
1446 + 24 | 2998 + 64 | 6822 + 184 | 151 | 147 | 145 | 1650 | 10950 | 86850 |
Таким образом, предложены два типа процессоров для АР анализа, которые при их реализации в ПЛИС дают возможность в реальном масштабе времени анализировать сигналы, дискретизированные с частотой до 300 МГц и имеют невысокие аппаратурные затраты. Внедрение процессоров дает возможность существенно расширить область применения АР-анализа, например, при ультразвуковой диагностике в медицине и машиностроении.
1. Марпл С.Л. Цифровой спектральный анализ и его приложения – М.: Мир, 1990. – 584с.
2. Brent R.P. Old and new algorithms for Toeplitz systems //Proc.SPIE, V.975, Advanced Algorithms and Architectures for Signal Processing III, SPIE, Bellingham, Washington, 1989. -Рр.2–9.
3. Bojanchuk A.W., Brent R.P. de Hoog F.R. Linearly Connected Arrays for Toeplitz Least-Squares Problems // J. of Parallel and Distributed Computing. 1990. N9. Pp.261-270.
4.Sergyienko A., Maslennikov O. Implementation of Givens QR Decomposition in FPGA //Lecture Notes in Computer Science, Springer, -Vol. 2328, 2002. -Рp. 453-459.
5.Клименко О.М., Сергієнко А.М., Шевченко Ю.В.,Овраменко С.Г. Конфігурована обчислювальна система для вирішення задач лінійної алгебри// Электронное моделирование, 2005, Т. 27, №1, с. 109-114.
6. Karlström P., Ehliar A., Liu D. High performance, low latency FPGA based floating point adder and multiplier units in a Virtex 4 // 24th IEEE Norchip Conf., Linköping, Sweden, Nov. 20-21, 2006. pp. 31-34.
7. Уидроу Б., СтиризС. Aдаптивная обработка сигналов – М.: Радио и связь. 1989. – 440с.
8. Pohl Z., Matoušek R., Kadlec J., Tichý M., Lícko M. Lattice adaptive filter implementation for FPGA //Proc. 2003 ACM/SIGDA 11-th Int. Symp., Monterey, California, USA, 2003. –Рp.246-250.
9. Hwang Y.T., Han J.C. A novel FPGA design of a high throughput rate adaptive prediction error filter // 1-st IEEE Asia Pacific Conf. on ASICs, AP-ASIC’99. 1999. –Pp.202 – 205.
10. Lin A.Y., Gugel K.S. Feasibility of fixed-point transversal adaptive filters in FPGA devices with embedded DSP blocks // 3rd IEEE Int. Workshop on System-on-Chip for Real-Time Applications (IWSOC’03). 2003. Pp.157-160.