Структурное проектирование рекурсивных цифровых фильтров

⇓Загрузить PDF (рус.)

Тр. межд. конф. “Автоматизация проектирования дискретных систем.” (CADDD’07). —Минск.—2007.–с. 92–99.

СТРУКТУРНОЕ ПРОЕКТИРОВАНИЕ РЕКУРСИВНЫХ ЦИФРОВЫХ ФИЛЬТРОВ

А. М. Сергиенко Национальный технический университет Украины КПИ, Киев, Украина;
О.В.Масленников Кошалинский политехнический институт, Кошалин, Польша

Рассмотрен метод проектирования структур цифровых фильтров путем отображения графа алгоритма, представленного в многомерном индексном пространстве и отображении его в подпространства структур и времени. Ограничения на процесс отображения позволяют минимизировать как тактовый интервал, так и аппаратные затраты, включая мультиплексоры при реализации фильтров в ПЛИС.

Введение

Программируемые логические интегральные схемы (ПЛИС) имеют емкость в миллионы вентилей и сотни блоков умножителей с аккумуляторами. Поэтому ПЛИС часто применяется для цифровой обработки сигналов (ЦОС). Получают распространение такие программные средства, как AccelDSP и System Generator для перевода алгоритма ЦОС в прошивку ПЛИС [1]. Но эти средства эффективны, в основном, для алгоритмов с ациклическими графами, при единичном отображении алгоритма или для алгоритмов, операторы которых соответствуют готовым библиотечным компонентам.

При системном синтезе вычислительных устройств (ВУ) алгоритм ЦОС представляют графом синхронных потоков данных (ГСПД – synchronous dataflow graph). В нем вершины – акторы представляют собой операторы, а дуги – передачи переменных между акторами с буферизацией в FIFO. Акторы в течение цикла генерирует и потребляет число переменных, которое неизменно от цикла к циклу [2],[3].

Синтез ВУ обычно выполняется в три этапа: выбор аппаратных ресурсов, составление расписания выполнения акторов и назначение акторов на ресурсы. Подграфы циклического ГСПД могут выполняться с различными периодами, как, например, в системе с несколькими частотами дискретизации (multirate system). Распространенный подход – это поиск расписания для периода алгоритма, когда вычисления планируются для его ациклической части. Здесь используются алгоритмы списочного планирования, силового планирования, метод планирования с выравниванием акторов по левому краю пространства ресурсы – время (left edge scheduling). Но прямое их применение приводит к низкой загруженности ВУ в начале и в конце цикла. Для учета цикличности алгоритма анализируют граф конфликтов ресурсов и операций и граф интервалов существования переменных [3],[4].

В работах [5],[6] предложены методы отображения алгоритмов, представленных ГСПД, в структуры параллельных ВУ. Методы основаны на размещении графа алгоритма в многомерном индексном пространстве и отображении его в подпространства структур и времени. Методы структурного проектирования цифровых фильтров (ЦФ), описанные в [6],[7] также используют этот подход. При таком подходе этапы синтеза выполняются почти одновременно и ВУ оптимизируется с удовлетворением противоречивых требований. В докладе описывается применение этого подхода к синтезу структур рекурсивных цифровых фильтров (ЦФ) для реализации в ПЛИС.

1. Отображение ГСПД в подпространства структур и времени

Исходные данные для проектирования ВУ – это алгоритм ЦОС в виде ГСПД и критерии оптимизации. Предполагается, что процессорный элемент (ПЭ) включает в себя умножитель или сумматор с регистром результата на его выходе и мультиплексорами на его входе. ПЭ выполняет операцию с записью результата в регистр не более, чем за такт. Если регистра нет, то считается, что операция выполняется без задержки.

Критерии оптимизации – период выполнения алгоритма Q_T = Lt_C и сложность ВУ Q_S =∑ С_p q^p, где L – число тактов периода алгоритма, t_C – длительность такта, С_p – сложность ПЭ p-го типа, q^p – число таких ПЭ. Средняя сложность входа мультиплексора ПЛИС фирмы Xilinx оценивается в 0,57 сложности регистра или АЛУ. Исходя из соотношения числа умножителей и конфигурируемых блоков в ПЛИС, и необходимости максимальной загрузки всех ее элементов, затраты 18-входового 16-битного мультиплексора в ПЛИС соответствуют затратам комбинационного умножителя такой же разрядности. Поэтому нужно минимизировать как число ПЭ, так и количество входов их мультиплексоров, которое также отражает сложность линий связи в ПЛИС.

ГСПД представляется в трехмерном целочисленном пространстве в виде конфигурации алгоритма (КА) K_G = (K,D,A), где K – матрица векторов-вершин K_i, соответствующих операторам алгоритма, D – матрица векторов-дуг, отвечающих непосредственным информационным связям между операторами, A – матрица инцидентности ГСПД. В векторе-вершине K_i = <k_i,s_i,t_i> координаты k_i,s_i,t_i равны типу оператора,номеру ПЭ, где выполняется оператор и такту, в котором записывается результат.

Различным эквивалентным структурным решениям ВУ соответствуют эквивалентные КА, которые отличаются лишь разными матрицами К и D. Можно сказать, что матрица К кодирует некоторое допустимое решение, так как матрица D вычисляется из уравнения D = КА. Поиск оптимального структурного решения заключается в нахождении такой матрицы К, которая минимизирует заданный критерий качества. Если применяется генетический метод оптимизации, то матрица К может служить геном представителя популяции. При поиске эффективных структурных решений необходимо руководствоваться следующими закономерностями.

КА является корректной, если в матрице К нет двух одинаковых векторов, т.е.

∀ K_i,K_j (K_i≠ K_j, i≠ j).

Расписание выполнения алгоритма – корректно, если операторы, отображаемые в один и тот же ПЭ, выполняются в различных тактах, т.е.

∀ K_i,K_j(k_i=k_j, s_i=s_j) ⇒ t_i¬≡t_j mod L.

Однотипные операторы следует отображать в ПЭ того же типа, т.е.

K_i,K_j ∈ K_p,q(k_i=k_j=p, s_i=s_j=q), |K_p,q| ≤ L,

где K_p,q – множество векторов-вершин операторов p-го типа, отображаемых в q-й ПЭ p-го типа (q=1,2,… q^p_max).

Если в ГСПД есть циклы, то должна быть равна нулю сумма векторов-дуг D_j, входящих в любой из циклов графа, т.е. для i-го цикла

∑ b_i,j D_j = 0,

где b_i,j – элемент i-й строки цикломатической матрицы ГСПД.

Такие циклы характерны для рекурсивных ЦФ, причем обратные векторы-дуги D_Вj = <0,0,–iL> означают задержку, равную i циклов (итераций). Они эквивалентны вершинам задержки Z^–i в сигнальном графе алгоритма ЦОС.

Эффективную КА ищут в два этапа. На первом этапе вершины ГСПД вместе с дугами размещаются в трехмерном пространстве как множества векторов K_i и D_j с учетом условий, приведенных выше, т.е. формируется начальная КА. Минимизируется число ПЭ в искомой структуре путем выполнения требования |K_p,q|→L, т.е. число вершин, отображаемых в один ПЭ, стремится к L. Также возможна перестановка вершин относительно оси времени оt, которая отвечает ресинхронизации ГСПД.

На втором этапе КА уравновешивается. Рассматривается ациклический подграф ГСПД без обратных дуг D_Вj. Во все его дуги включаются промежуточные вершины операторов задержки (регистров). В результирующей уравновешенной КА все векторы-дуги, кроме обратных дуг, равны D_j=<a_j,b_j,1> или D_j=<a_j,b_j,0>. При этом вершины-операторы образуют ярусы, расстояние между которыми по координате времени оt равно 1 такт. Уравновешенная КА оптимизируется путем взаимных перестановок векторов-вершин, принадлежащих одному ярусу с минимизацией числа регистров и входов мультиплексоров. Применяются и другие стратегии, например, алгоритм левого края.

Структуру ВУ и расписание выполнения алгоритма можно получить, расщепив КА K_G на конфигурацию структуры (КС) K_S и конфигурацию предшествования (КП), которые имеют ту же матрицу А, а векторы матрицы K_S координат ПЭ и матрицы моментов срабатывания K_T равны координатам векторов матрицы К, т.е. <k_i,s_i> и <t_i>. КС и КП представляют собой отображение КА в подпространства структур и времени, которое выполняется элементарным образом.

2. Метод минимизации мультиплексоров

Рассмотрим метод минимизации числа мультиплексоров в конвейерных ВУ, который дает положительный эффект для проектов ЦФ в ПЛИС. В большинстве случаев ГСПД алгоритмов ЦОС имеют изоморфные подграфы. Так, алгоритмы рекурсивных ЦФ – это цепочки из одинаковых ступеней второго порядка. Для минимизации входов мультиплексоров можно использовать следующие утверждения.

Утверждение 1. Для согласованной КА количество входов N_Мi мультиплексоров i – й вершины ПЭ не больше количества неодинаковых векторов D_і,j, инцидентных вершинам K_i,k, которые отображаются в эту вершину ПЭ.

Доказательство утверждение очевидно. Выражение “не больше” означает тот случай, когда не больше чем с одного входа ПЭ подается операнд на один вход АЛУ
этого ПЭ, и тогда для такого входа мультиплексор не нужен.

Утверждение 2. Пусть ГСПД согласованной КА имеет до L изоморфных подграфов, которые представлены эквивалентными подконфигурациями K_GОі=(K_Оі,D_Оі,A_O). Тогда для того, чтобы при отображении этой КА в структуру с конфигурацией K_S и периодом вычислений L получалось минимальное количество ПЭ и входов их мультиплексоров, необходимо и достаточно, чтобы все подконфигурации i>K_GОі отображались в одну подконфигурацию структуры K_SO, причем

∀K_i,j∈K_Оі(K_i,j= <C_j,k,C_j,l, t_i,j>);    (1)
∀K_i,j∈K_Оі(arrow of D_i,l is incident to K_i,j ⇒ D_i,l= <C_k,C_l, 1>, C_l≠0 ).    (2)

Условия означают, что подграф структуры изоморфен подграфам алгоритма. На рис. 1 показан пример отображения КА с периодом L = 3 в соответствующую КС. На нем толстой чертой обозначен мультиплексор.

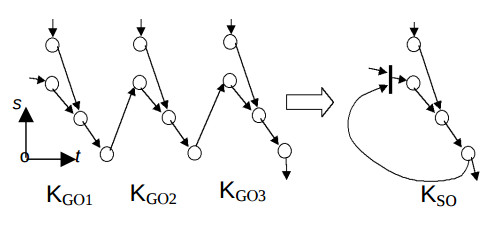
Нетрудно показать что при выполнении условий (1) и (2) ПЭ с одновходовым АЛУ будет иметь один вход, а с двовходовым АЛУ – соответственно 2 входа. То есть
каждый ПЭ, кроме ПЭ ввода-вывода этой подструктуры, совсем не имеют мультиплексоров, и эти условия – условия достаточности.

Пусть одна или две из вершин-операторов будут переставлены, т.е. тогда не выполняются условия (1),(2). Возможны две ситуации. В первой – одна переставленная вершина отобразится в новую вершину ПЭ, т.е. увеличатся аппаратные затраты на один ПЭ. Кроме того, вектор D_i,l, который выходит из этой вершины, изменит свои координаты и не будет равен вектору D_i,k, который до этого вместе с ним отражался в одну дугу структуры. Поэтому должен быть добавлен мультиплексор в ПЭ, в который поступает результат с нового ПЭ. В второй ситуации вершина будет отображена в другой, не полностью занятый ПЭ или две вершины будут взаимно переставлены. Тогда на входах АЛУ этих ПЭ должны появиться двувходовые коммутаторы. Таким образом, любые изменения в подконфигурациях, которые нарушают условия (1),(2) приводят к увеличению количества ПЭ или входов мультиплексоров, т.е. эти условия − необходимые.

3. Методика синтеза ЦФ с кратными задержками

Известно, что каждому члену Z^-k в формуле характеристики ЦФ H₀(Z) отвечает цепочка из k регистров задержки. Если в ЦФ количество регистров задержки увеличить в n раз, то получим ЦФ с кратными задержками с характеристикой H_n(z) = H₀(Zⁿ). У этого фильтра АЧХ по форме такая же, как у фильтра-прототипа H₀(Z), но в диапазоне 0 – f_S она повторяется n раз, где f_S – частота дискретизации.

При последовательном соединении ступеней ЦФ результирующая АЧХ – это пересечение АЧХ ступеней. При этом говорят, что АЧХ маскируют друг друга. Путем
маскирования и использования ЦФ с кратными задержками получают высокодобротные фильтры с минимальными аппаратными затратами [8]. Кроме того, фильтры с кратными задержками – это эквивалент фильтра с несколькими частотами дискретизации. В ПЛИС фирмы Xilinx кратные задержки исполняют на FIFO типа SRL16, которые занимают столько же места, как и отдельные регистры. Для синтеза таких фильтров на базе ПЛИС предлагается следующая методика.

На первом этапе выбирается алгоритм, ГСПД которого имеет изоморфные подграфы, отличающиеся тем, что задержки, какими нагружены их дуги, кратны и равны К. Если число таких подграфов равно L, то это обеспечивает максимальную загруженность результирующей структуры. Подграф алгоритма с К=1, представляется в виде конфигурации периода алгоритма (КПА). В КПА выделяются пограничные вершины, в которые заходят и с которых выходят обратные векторы, которые соответствуют задержкам на К итераций. Эти пограничные вершины далее будут отображены в итерационные входы и выходы структуры. КПА оптимизируется с условием, что она отображается в структуру с периодом вычислений L=1 тактов.

На втором этапе до L КПА соединяются между собой в соответствии с алгоритмом фильтрации соблюдением условия утверждения 2. Так как в некоторой ступени используются задержки на К тактов, то к ее КПА добавляются подконфигурации задержек на К-1 периодов, которые через обратные векторы длиной LK подсоединяются к пограничным вершинам. Также добавляются вершины операторов и дуги, которые дополняют КПА, подконфигурации задержек до полного ГСПД.

На третьем этапе КА отображается в структуру с периодом вычислений L. Результирующая структура включает в себя структуру, отвечающую КПА, к
итерационным входам которой подключены мультиплексоры, к входам которых через задержки на К-1 периодов подаются задерживаемые данные.

Аппаратные затраты ВУ включают затраты на построение конвейерной структуры, в которую отображается КПА, мультиплексоры с числом входов до L и задержки на различное количество периодов – от 0 до К-1. При этом сама конвейерная структура мультиплексоров не имеет. Аппаратные затраты, выраженные в сложности сумматора, не считая числа регистров, можно определить по формуле:

Θ’_S = n_A + 10n_M + 0,57Ln_D ,

где n_A и n_M– число сумматоров и блоков умножения, которое равно числу сложений и умножений в алгоритме ступени; n_D – число переменных, по которым выполняются межитерационные связи, т.е. число линий задержек в ступени фильтра.

Количество регистров в структуре зависит от топологии ГСПД ступени фильтра, распределению длины задержек К среди ступеней и пропорционально L. Таким образом, структура при количества ступеней, равном L, имеет минимальное число регистров, сумматоров и блоков умножения. Это утверждение выходит из того, что ровно L вершин операторов задержки, операторов сложения и умножения отображаются в одну вершину регистра, сумматора, блока умножения, соответственно. Т.е. ресурсы структуры асимптотически загружены на 100%.

4. Пример синтеза рекурсивного ЦФ

Рассмотрим пример синтеза ЦФ нижних частот, состоящего из четырех ступеней с задержками кратности 1,2,4 и 8. Первые 3 ступени – это полуполосные ЦФ, а
последняя ступень – фильтр-формирователь. Полуполосный ЦФ имеет АЧХ фильтра-дециматора, но не выполняет собственно децимацию. Благодаря тому, что эти ЦФ с кратными задержками и выполняется маскирование, результирующая АЧХ имеет узкую переходную полосу [5]. Каждая ступень построена на фазовом ЦФ, благодаря чему получаются высокие и стабильные характеристики фильтра, а также возможность их регулирования. Передаточна функция одной (первой) ступени фильтра равна:

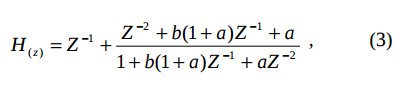
где b – регулирует частоту среза, a – регулирует крутизну спада [8].

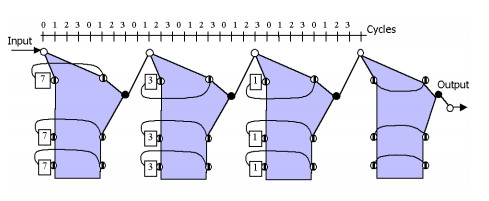
На первом этапе синтеза структуры ЦФ формируется уравновешенная КПА, (рис.2). Она соответствует волновому фильтру, имеющему передаточную характеристику (3). На рисунке вершины регистров показаны большими, кружочками, обратные векторы – разрывной стрелкой, а пограничные вершины – полузакрашенными кружочками.

На втором этапе L=4 КПА соединяются между собой последовательно. Результирующая КА показана на рис. 3. На нем закрашенные многоугольники – это КПА. На третьем этапе получается структура фильтра и синтезируется его управляющий автомат. Полученная конфигурация структуры фильтра показана на рис.4. Реализация фильтра состоит в его описании на языке VHDL и дальнейшем отображении в ПЛИС. При этом используется методика отображения КА в ПЛИС, которая описана в [6].

При построении ЦФ традиционным способом он будет иметь 4 ступени по 7 сумматоров, 2 блока умножения и 3 регистра каждая. Ступени также имеют по 3 задержки длиной 1,2,4 и 8 регистров. Результирующие аппаратные затраты Θ_SВ = 132. В критический путь входят 4 сумматора, т.е. период тактового интервала составляет Θ_ТВ = 4Т_S. Синтезированная структура имеет 2 блока умножения, 7 сумматоров, 26 регистров и регистровых задержек, а также 1 двовходовый и 6 четырехвходовых мультиплексоров.

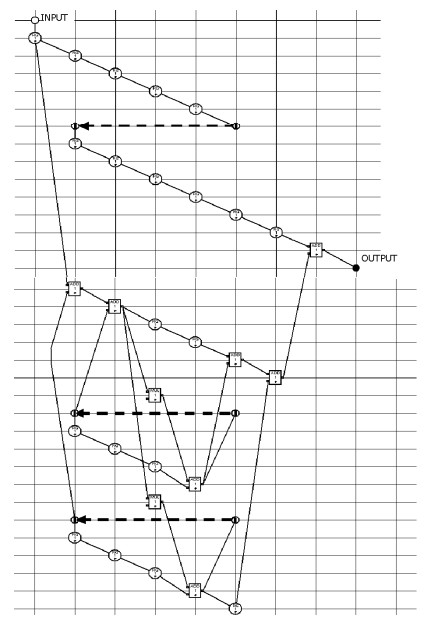
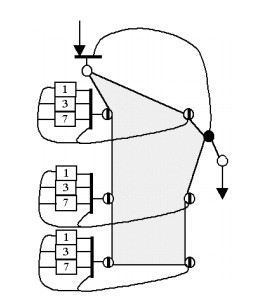
Аппаратные затраты ЦФ составляют Θ_S=65,5. Период тактового интервала равен Θ_Т = Т_S, т.е. в критический путь входит задержка сумматора или умножителя, а длительность цикла LТ_S=4Т_S. Следовательно, полученный ЦФ имеет вдвое меньшие аппаратурные затраты, чем традиционная структура, при той же производительности.

5. Цифровой фильтр с динамической перестройкой частоты среза

На основе ЦФ с кратными задержками и фазовых ЦФ был разработан ЦФ со структурой на рис. 4. В фильтре перестраивается частота среза скачками – отводом сигнала от той или иной ступени, а также плавно – изменением коэффициентов ступени, от которой выполняется отвод. В результате, частота среза динамически изменяется плавно в пределах (0,015-0,4)f_S. За счет того, что число ступеней увеличено до L=8, при любой заданной частоте среза уровень подавления составляет не менее 80 дб, а наклон АЧХ в переходной полосе – не менее 100 дб/октава.

Для задания частоты среза 12-битным кодом, разработан аппаратный калькулятор, пересчитывающий код частоты в значение коэффициентов ЦФ. ЦФ был реализован в ПЛИС Xilinx Virtex2P. Его аппаратные затраты без калькулятора коэффициентов составляют 706 CLB slices и 3 блока умножения. Благодаря высокой степени конвейеризации структуры, тактовая частота достигает 190 МГц. Таким образом, фильтр может обрабатывать в реальном времени сигналы с частотой дискретизации до 24 МГц.

6. Арифметика рациональных дробей в рекурсивных ЦФ

Высокодобротные рекурсивные ЦФ для своей реализации требуют повышенной разрядности данных. Поэтому для реализации таких ЦФ обычно удваивают длину разрядной сетки или используют плавающую запятую. В результате – возрастают аппаратурные затраты и/или снижается производительность ВУ.

Предлагается выполнять вычисления рекурсивных ЦФ в арифметике рациональных дробей [9]. При этом данные представляются в виде числителя и знаменателя.
Умножитель рациональных дробей имеет 2 обычных умножителя, т.е. он вдвое проще, чем умножитель удвоенной разрядности. Сумматор дробей имеет 3 умножителя и 1 сумматор целых чисел. Для сохранения точности после каждой операции выполняется нормализация числителя и знаменателя на небольшое число разрядов (2-4). Недостатком является то, что в конце вычислений приходится вычислять обратную величину знаменателя и умножать на нее числитель, чтобы представить результаты в целых числах. Но если система ЦОС выполняет сложные алгоритмы, включая многочастотную многоканальную фильтрацию, решение систем уравнений, БПФ, то преобразование в целые числа имеет незначительную относительную сложность.

АЛУ с арифметикой дробей имеет большие аппаратурные затраты, чем АЛУ для целых чисел. Однако эти затраты в 2-4 раза меньше, чем при реализации плавающей запятой а его пропускная способность выше, чем у АЛУ с удвоенной разрядностью или с плавающей запятой. Хотя конвейерная задержка такого АЛУ больше, чем у АЛУ целых чисел (4-6 тактов), она существенно ниже, чем у АЛУ с плавающей запятой.

При использовании такого АЛУ в рекурсивном ЦФ традиционной структуры, его производительность будет слишком мала из-за большой конвейерной задержки, которая будет входить в критический путь. Зато при проектировании такого ЦФ предложенным методом его положительные свойства проявятся лучшим образом.

Заключение

Описан метод проектирования конвейеризованных ВУ для ЦОС, который обеспечивает минимизацию как числа АЛУ, блоков умножения, так и количества входов мультиплексоров благодаря использованию как особенностей алгоритмов ЦОС, так и структурных свойств современных ПЛИС. При этом синтезированное ВУ имеет минимальный период тактового интервала при выполнении алгоритма ЦОС в конвейерном режиме с заданным периодом вычислений L.

Разработаны метод и методика проектирования многоступенчатых цифровых фильтров с кратными задержками, которая обеспечивает при заданных ограничениях (период L, элементная база, ГСПД с изоморфными подграфами) минимальные период синхросерии и апаратные затраты. Проверка методики при проектировании многоступенчатых волновых фильтров показала, что можно уменьшить аппаратные затраты вдвое при такой же производительности по сравнению с традиционным проектированием.

Предложено выполнение рекурсивных ЦФ на основе арифметики рациональных дробей, что при использовании новой методики, позволит выполнять высококачественную фильтрацию на малом оборудовании с достаточно высокой скоростью.

Список литературы

1. http:/www.xilinx.com

2. Bhattacharyya S.S., Leupers R., Marwedel P. Software Synthesis and Code Generation for Signal Processing Systems // IEEE Trans. on Circuits and Systems—II: Analog and Digital Signal Processing, − 2000. −V47. −№9. −p.849-875.

3. The Systhesis Approach to Digital System Design / Ed. P. Michel, U.Lauther, P.Duzy. Kluwer Academic Pub. −1992. −415 p.

4. Eles P., Kuchinski K., Zebo P. System Synthesis with VHDL. Kluwer Academic Pub.-1998.−370 p.

5. Каневский Ю.С., Овраменко С.Г., Сергиенко А.М. Отображение регулярных алгоритмов в структуры специализированных процессоров // Электрон. Моделирование.−2002.−Т.24.−№2.−С. 46-59.

6. Сергиенко А.М. VHDL для проектирования вычислительных устройств. –Киев: ДиаСофт. –2003. –208 с.

7. Каневский Ю.С., Логинова Л.М., Сергиенко А.М. Структурное проектирование рекурсивных цифровых фильтров. // Электрон. Моделирование. –1995. –Т.17. −№ 3, −С. 18-22.

8. Chung J. G., Parhi K. K. Pipelined wave digital filter design for narrow-band sharptransition digital filters // Proc. IEEE Workshop VLSI Signal Processing, La Jolla, CA. −1994. −pp. 501-510.

9. Сергиенко А.М. Применение арифметики рациональных дробей для реализации метода сопряжения градиентов // Электрон. моделирование. – 2006, Т. 28, № 1.− С. 33-41.

This work was partially supported by the Polish Ministry of Science and Higher Education under grant N515 002 32/0176.

⇓Загрузить PDF (рус.)