VHDL против Matlab’a
Argc&Argv. Программирование / информационные технологии / стандарты. 2005, № 1(58), стр. 40-46.
VHDL против Matlab’а
А.М. Сергиенко
Два десятилетия назад широкому распространению персональных ЭВМ способствовал язык Бейсик. Начинающий пользователь мог быстро освоить язык и начать решать свои несложные задачи в интерактивном режиме. Пользователям – математикам этого оказалось мало – и для них была разработана программа и язык Matlab.
Автор познакомился со второй версией Matlab’a полтора десятилетия назад. Это был пакет программ и библиотек, который в минимальной конфигурации помещался на одной дискете и исполнялся под MS DOS. После краткого периода его освоения стало ясно – Matlab–это Бейсик, оперирующий с векторами и матрицами, поддержаный большой математической библиотекой.
За прошедшие годы сменилось несколько версий Matlab’а, добавилось большое количество возможностей графического интерфейса, подсказок и других атрибутов
дружественного интерфейса. Matlab занял монолитный сектор рынка такого рода программ.
Сейчас Matlab повсеместно используется для экспериментального численного решения многих математических задач. В большинстве случаев с помощью его выполняется исследовательское численное моделирование явлений различной природы, как, например, процессы в электрических сетях, задачи акустики, прочности, гидродинамики. С точки зрения области приложений Matlab – “всеядная” система.
Для решения задач цифровой обработки сигналов к Matlab’у был добавлен пакет Signal, а затем для моделирования систем авторегулирования – подсистема Simulink. При этом Matlab не только красиво вырисовывает графики результирующих сигналов, но, например, рассчитывает коэффициенты фильтров, предлагает типичные решения. Иногда Matlab – программа используется в реальном масштабе времени в индустриальных приложениях. В этом случае она транслируется в объектный код [1].
В области цифровой обработки сигналов Matlab получил такое широкое распространение, что сейчас он становится стандартом для задания алгоритма работы устройства на системном уровне. Дошло до того, что Matlab -программа цифровой обработки сигналов транслируется в ассемблерную программу для сигнального микропроцессора. Уже такая программа воспринимается, как входные данные, некоторыми системами синтеза логических схем для ПЛИС. Т.е. в этом случае Matlab конкурирует с VHDL и Verilog, как язык для описания устройства на системном уровне.
Таким образом, современный разработчик аппаратных систем обработки сигналов наравне с языком VHDL должен пользоваться Matlab’ом. Но обязан ли? И может ли он обойтись одним VHDL?
Чтоб ответить на эти вопросы проведем сравнительный анализ Matlab’а и VHDL. Критерием сравнения будет пригодность и эффективность языка для моделирования задач цифровой обработки сигналов, описанных на верхнем – системном уровне.
Принцип моделирования. Основные операции в Matlab’e – это операции над векторами и матрицами. Например, фильтрация – это умножение вектора отсчетов сигнала на теплицеву матрицу импульсной реакции, выполняемое по встроенной подпрограмме свертки. Поэтому моделирование в Matlab’e – синхронное и прерывистое. Синхронное, т.к. предполагается, что данные поступают в равноотстоящих тактах, а прерывистое, т.к. порции моделируемых данных и результатов ограничены заранее заданными размерами массивов. Моделирование выполняется поэтапно – прежде чем начать выполнение следующего этапа обработки, необходимо завершить предыдущий этап и сохранить его результаты в промежуточном массиве.
При этом редко, когда размер массива превосходит миллион. Это означает, что без дополнительных усилий по “сращиванию” соседних порций данных можно моделировать процессы, длящиеся не более 1млн. тактов. И эта величина сокращается пропорционально сложности алгоритма, т.к. для хранения промежуточных массивов может не хватить памяти компьютера.
Если требуется моделирование системы с различными частотами дискретизации (multirate system), то приходится приводить частоты дискретизации к одной кратной частоте. Например, если 2 смежных блока работают с частотами дискретизации 8 и 11,025 кГц, то для получения 1 отсчета результата необходимо проcчитать не менее 320 тактов.
Проблема больших массивов решена в подсистеме Simulink, без которой не обойтись при моделировании систем с обратными связями. При этом алгоритм представляется графом синхронных потоков данных, отображаемый на экране в виде граф – схемы. Этот граф исполняется программно, так что за один моделируемый такт обрабатывающие блоки – вершины графа исполняют свои функции и обмениваются порциями данных, относящимися к этому такту. Т.е. здесь моделирование – событийное. Однако при этом теряется быстродействие скоростной обработки векторов и матриц, присущее Matlab’у.
VHDL- моделирование – также событийное. Данные обрабатываются в процессах, которые запускаются, как только приходят для них входные данные. Все временные
соотношения можно отслеживать очень точно – с точностью до фемтасекунды. Моделирование – непрерывное (не прерывистое) с любыми частотами дискретизации данных. Под промежуточные переменные и сигналы отводится небольшой объем памяти, который необходим для хранения соответствующих данных только в течение одного такта. Только под сигналы, которые выводятся в виде графиков, симулятором заводятся динамические массивы, максимальный размер которых определяется объемом винчестера. Поэтому VHDL – модель можно моделировать очень долго – многие миллионы, а иногда и миллиарды тактов.
Скорость моделирования. Синхронное моделирование – самое быстрое временное моделирование. В Matlab’е такие процедуры, как свертка, БПФ, перемножение и обращение матриц, выполняются по быстродействующим встроенным процедурам, что еще более ускоряет моделирование. Но есть причины, сдерживающие рост скорости моделирования.
Matlab – универсальная система. И она не была адаптирована под задачи обработки сигналов, как например, аналогичная система Elanix System View. Система Matlab не испытывала особенной конкуренции со стороны других аналогичных систем, как например, Mathcad, Maple, так как у всех таких систем различные языки программирования и они заняли отдельные потребительские ниши. Поэтому не было особенной необходимости оптимизировать быстродействие системы при моделировании обработки сигналов. Кроме того, в обычном режиме Matlab продолжает оставаться интерпретатором.
Событийное моделирование на 2-4 порядка медленнее синхронного моделирования. Но фирмы-поставщики VHDL-симуляторов, благодаря конкурентной борьбе между собой, вынуждены постоянно повышать скорость своих симуляторов. С другой стороны, индустрия СБИС остро нуждается в повышении быстродействия симуляторов и поэтому настойчиво стимулирует этот процесс.
Например, современный симулятор распознает, что данный модуль может быть промоделирован синхронно и переводит его в режим синхронного моделирования. В этом режиме моделирование может ускориться на 2 порядка. Современные VHDL-симуляторы обеспечивают моделирование проекта на параллельной системе из нескольких компьютеров, соединенных в локальную сеть, что также ускоряет этот процесс.
Если VHDL-модель описана синтезируемым стилем, то ее можно моделировать с помощью аппаратного ускорителя, основанного на конфигурировании ПЛИС. Такое
моделирование дает ускорение от десятков до десятков тысяч раз.
Представление данных. В подавляющем большинстве случаев в Matlab’e используются данные с плавающей запятой с двойной точностью. Только некоторые модули подсистемы Simulink работают с фиксированной запятой с разрядностью 8,16 или 32 бита, чтобы приблизить моделирование алгоритмов обработки сигналов к их исполнению в сигнальных микропроцессорах.
Моделирование с плавающей запятой избавляет программиста от проблем масштабирования, переполнения и потери точности при вычислениях. Но постоянное использование плавающей запятой развращает программиста, который уже не стремится подобрать оптимальный по точности и сложности алгоритм. И тогда необходимо прикладывать серьезные усилия для замены в алгоритме плавающей запятой на фиксированную. Часто в результате этого приходится выбирать дорогостоящий сигнальный микропроцессор с плавающей запятой, так как не хватает сил, чтобы переложить алгоритм на фиксированную запятую. Нередко для ускорения обработки сигналов по алгоритмам, полученным с помощью Matlab’a, в промышленных приложениях применяют многопроцессорные рабочие станции.
VHDL обеспечивает моделирование с данными в любом представлении, в том числе с плавающей и фиксированной запятой. Правда, точность плавающей запятой стандарт VHDL не регламентирует. Но в большинстве случаев, если в современном симуляторе промоделировать оператор
constant maxreal: real:=real'high;
то в результате получится максимальное число с плавающей запятой с двойной точностью:
maxreal = 1.0000E+308.
Числа с фиксированной точкой представляются как целые со знаком или как векторы битов. В последнем случае возможно моделирование обработки данных произвольной разрядности.
Обработка целых чисел в VHDL имеет следующие полезные особенности:
– можно любую переменную или сигнал задать с диапазоном, тогда выход переменной за границы диапазона, например, при переполнении, вызовет остановку симулятора. Это соответствует заданию разрядности операндов с точностью до бита. Такое ограничение также удобно при отладке алгоритма и коррекции масштабных коэффициентов. Причем соответствие диапазонов операндов и результатов операций, как в случае векторов битов, необязательно, поэтому
– программирование с целыми числами проще, чем с векторами битов, что подтверждается также тем, что не нужно использовать функции преобразования типов и/или типы signed, unsigned;
– моделирование с целыми числами происходит заметно быстрее, чем с векторами битов или с числами с плавающей запятой;
– целые числа занимают в памяти существенно меньше места, чем векторы битов или числа с плавающей запятой;
– проекты с переменными и сигналами целого типа, особенно с диапазонами, могут быть без всяких изменений странслированы в логическую схему и далее – в ПЛИС, и их моделирование многократно ускоряется аппаратными ускорителями;
– целые числа ближе к архитектуре большинства сигнальных процессоров, чем числа с плавающей запятой, поэтому модель с целыми переменными легче переделать в программу для такого процессора.
К сожалению, не всегда достаточно разрядности 32-разрядных целых чисел, применяемых в большинстве симуляторов. Только некоторые из симуляторов используют 64-разрядные целые числа.
Как в Matlab’e, так и в VHDL применяются одномерные и многомерные массивы. Отличие в том, что в Matlab’e разреженные матрицы можно представлять в компактном виде. Но это удобно для решения уравнений в частных производных, а не большинства задач цифровой обработки сигналов. Иногда вызывает неудобство то, что массивы в Matlab’e начинают индексацию с 1, а не с 0.
Зато в VHDL можно вводить всевозможные типы пользователя. Так, в известном пакете IEEE_Math_Complex введен комплексный тип. В [2] используется тип рациональных дробей, над которым определены такие арифметические операции, как + |/ |*. В [3] для разработки устройств на троичной логике введен тип троичных чисел.
Библиотеки функций и процедур. Нет такой общепринятой математической функции, которой бы не было в библиотеке Matlab’a. Многие процедуры и функции выполнены в странслированном с языка Си виде для своего быстрого исполнения.
Но библиотека процедур и функций подсистемы Simulink – ограничена. Если требуется подсоединить блок своей собственной конструкции, исполняемый как процесс, то его следует описать на языке Си, Фортран или Aдa и в странслированном виде подключить к библиотеке особенным образом.
Следует сказать, что VHDL – это младший брат Aды. Он от нее отличается, в частности, тем, что быстродействие VHDL –программ и количество параллельных процессов в них может быть намного больше. Это достигнуто благодаря тому, что VHDL, в отличие от Ады, не занят решением проблемы конфликтов при доступе к глобальным переменным.
Для математических расчетов, необходимых в моделировании обработки сигналов, VHDL имеет библиотеки IEEE_Math_Real и IEEE_Math_Complex. Однако в них нет таких процедур, как решение систем уравнений, нахождение корней полиномов, расчета коэффициентов фильтров, быстрого преобразования Фурье (БПФ), которые часто необходимы при разработке систем цифровой обработки сигналов и которые есть в Matlab’e.
Зато в VHDL нет проблем с расширением и добавлением различных библиотек. Сам VHDL – это очень маленькое ядро с предопределенными типами и операциями и большим числом библиотек и пакетов, некоторые из которых приняты в виде международных стандартов.
Функция, процедура или объект, обозначенные атрибутом foreign, могут быть исполнены любым способом, например, как программа на Си или как внешнее специализированное устройство.
В последнее время для моделирования аналого-цифровых (Analog-Mixed Signal) систем получает распространение VHDL-AMS. Это расширенный VHDL, позволяющий
дополнительно вести моделирование аналоговых частей проекта путем решения разреженных систем уравнений [4].
Графическое представление данных. В Matlab’e сделано почти всё, чтобы можно было представить любые данные удобными для восприятия глазом. Особенно это касается представления многомерных массивов.
К сожалению, VHDL-симуляторы предоставляют более чем скромные средства представления численных данных. Только сравнительно недавно стало возможным
представлять численные сигналы в виде графиков с осью аргументов как осью времени, а двумерные массивы – в виде матриц, да и то – как дамп памяти. Зато такие графики могут содержать до миллионов точек, и их просто и быстро масштабировать и просматривать. Причем, точки графиков могут отстоять друг от друга неравномерно, и график сохраняется в ПК в упакованном виде. И еще немаловажно, что вывод больших графиков выполняется намного быстрее, чем у Matlab’а. Доступ к любому участку графика, занимающего несколько гигабайт винчестера, выполняется почти с такой же скоростью, как и к короткому графику.
Как резюме, в VHDL-симуляторе плохие возможности по графическому представлению данных. Разве что, пользователь может записать интересующие данные в файл и затем отобразить их с помощью какой-либо посторонней системы отображения данных, например, того же Matlab’а.
Средства графического программирования. Как Matlab, так и симуляторы VHDL имеют в своем составе средства графического программирования. Структурный стиль программирования на VHDL взаимно однозначно соответствует программированию в виде вырисовывания блок-схемы некоторого виртуального устройства. Пользователю предоставляется возможность самому создать графический дизайн его новых элементов. Также автоматные алгоритмы могут представляться в виде диаграммы своих состояний.
Как и большинство современных оконных систем, VHDL-симулятор может управляться и программироваться с помощью макроязыка, такого как Visual Basic, Perl или TCL. При желании, с помощью программы на макроязыке можно к симулятору “привязать” такие функции, которые в нем не предусмотрены, например, свою программу для графического представления данных.
Выводы.
1. У VHDL достаточно много возможностей, чтобы проектировать системы обработки сигналов на высоком уровне без использования таких средств, как Matlab. Это скоростное событийное моделирование довольно длительных и трудоемких алгоритмов, представление данных с плавающей и фиксированной точкой, в том числе с экстремально большой разрядностью, наличие библиотек математических функций и возможность графического представления данных.
2. Большинство систем исследования численных алгоритмов и алгоритмов обработки сигналов, включая Matlab, ориентированы на обработку с плавающей запятой. VHDL-симулятор может с ними конкурировать при моделировании алгоритмов обработки сигналов с целыми числами, так как он выполняет эту обработку наиболее эффективно и от такого представления проще переход к аппаратной или программной реализации этих алгоритмов.
3. Для эффективного использования VHDL-симулятора при разработке алгоритмов и устройств обработки сигналов, необходимо, во-первых, разрабатывать пакеты процедур и функций, аналогичных таким, которые применяются в Matlab’e для этих целей, во-вторых, создавать удобные условия для отображения одно- и двумерных сигналов в графическом виде.
Пример блока БПФ
Чтобы оценить возможности VHDL при исследовании алгоритмов цифровой обработки сигналов и начать на практике их использование, рассмотрим разработку и применение блока для вычисления БПФ.
Процедура БПФ широко используется в цифровой обработки сигналов для получения амплитудного и фазового спектров сигнала, а также для свертки длинных последовательностей отсчетов сигналов. В Matlab’е встроена процедура FFT, которая вычисляет БПФ для массива N комплексных данных с плавающей запятой. Если N равно степени двойки, то эта процедура выполняется довольно быстро. Результаты БПФ можно получить в виде графиков, выполнив процедуру PLOT.
В симуляторах VHDL обычно цифровые сигналы поступают, вырабатываются и наблюдаются в виде графиков, получаемых в процессе моделирования алгоритма. Но алгоритм БПФ предполагает, что данные поступают и выдаются сразу в виде массивов. Также многие другие алгоритмы обработки, как, например, решение систем уравнений, требуют аналогичного поступления данных. Поэтому целесообразно вычислять БПФ как цепочку процедур. Первая из них, называемая Gather_С, накапливает входной массив комплексных исходных данных. Вторая процедура – FFT – выполняет алгоритм БПФ, а заключительная процедура Scatter_С выдает результирующий массив в виде последовательности данных.
Указанные процедуры выполняются объектом FFTbeh. Этот объект можно вставлять в нужное место разрабатываемого проекта, как компонент, с целью измерить спектр интересующих сигналов или отобразить сигнал из временной области в частотную. Интерфейс этого объекта и перечень используемых стандартных библиотек выглядит так:
library IEEE;
use IEEE.std_logic_1164.all;
use IEEE.std_logic_ARITH.all;
use IEEE.MATH_REAL.all;
use IEEE.MATH_COMPLEX.all;
entity FFTbeh is
generic(
N:positive:=8; -- 2**N -длина преобразования
IDCT:natural:=0; -- 0- прямое, 1- обратное преобразование
PT:natural -- масштаб результата =2**PT
);
port (
CLK: in STD_LOGIC; -- синхросерия
RST: in STD_LOGIC; -- асинхронный сброс
START: in STD_LOGIC; -- начало накопления входного массива
EDIN: in STD_LOGIC; -- строб данных
DIN_RE: in integer; -- реальная часть данных
DIN_IM: in integer; -- мнимая часть данных
DOUT_RE: out integer:=0;-- реальная часть спектра
DOUT_IM: out integer:=0;-- мнимая часть спектра
NUM: out integer:=0; -- номер выходного отсчета
READY: out STD_LOGIC -- начало вывода результатов
);
end FFTbeh;
В библиотеках IEEE.MATH_REAL и IEEE.MATH_COMPLEX хранятся объявление типа комплексного данного, такие функции, как синус, косинус, квадратный корень, функции от комплексных аргументов и другие, которые применяются для вычисления БПФ.
Настроечная переменная N задает длину преобразования. При IDCT = 0 выполняется прямое преобразование, а при 1 – обратное. Переменная PT задает масштаб результата. Таким образом, преобразование равно
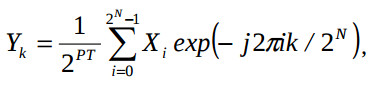
где Xi – отсчет входных комплексных данных: DIN_RE +j*DIN_IM, Yk – отсчет комплексного спектра: DOUT_RE +j*DOUT_IM.
По сигналу, приходящему в порт START, начинается накопление массива входных данных. Окончание вычислений БПФ указывается сигналом с выходного порта READY. Выдаваемые отсчеты спектра сопровождаются номером отсчета NUM, по которому удобно находить значение частоты той или иной спектральной линии.
Различные блоки обработки сигналов целесообразно выполнить с интерфейсом, аналогичным интерфейсу объекта FFTbeh. Тогда их можно соединять между собой
последовательно в соответствии с основным алгоритмом. При этом выходной порт READY одного блока соединяется с входным портом START следующего блока.
Сигнал на порте EDIN стробирует прием входных данных. В общем случае, этот сигнал разрешает работу блока в отдельных тактах. Это необходимо для моделирования и стыковки блоков, работающих с взаимно кратными периодами дискретизации. Например, с помощью блока FFTbeh можно определять узкополосный спектр после предварительной фильтрации полосовым фильтром и снижения частоты дискретизации в М раз. При этом сигнал EDIN должен иметь скважность 1:М.
Поведение объекта FFTbeh описано в архитектуре FFT_int. Для представления массивов данных в ней объявлены следующие типы массивов комплексных и действительных данных.
constant NN: integer:=2**N; -- длина преобразования type MEMOC is array (0 to NN) of complex; --комплексный массив type MEMOC_2 is array (0 to NN/2-1 ) of complex; type MEMOR is array (0 to NN-1) of real; --вещественный массив
В следующем тексте описана процедура, по которой накапливается массив входных
комплексных данных.
procedure GATHER_C(signal CLK,START,EDIN:in std_logic;
signal DR,DI: in integer; --реальная и мнимая часть отсчетов входных данных
signal rdy: out std_logic; --сигнал готовности
signal datact: inout natural;--номер данного
signal RAM:out MEMOC) -- рабочий массив
is
variable TR,TI:real;
begin
wait until CLK= '1'; -- запуск процедуры по фронту CLK
if EDIN = '1' then -- проверка разрешения приема
TR:= real(DR); -- формирование комплексного данного
TI:= real(DI);
RAM(datact)<=(TR,TI); -- и запись его в массив
if datact < RAM'right then
datact<=datact+1; -- счетчик данных
end if;
if START='1' then
datact<=RAM'left; --обнуление счетчика данных
end if;
rdy<='0';
if datact =RAM'right-1 then
rdy<='1'; --массив готов
end if;
end if;
end procedure;
Такая процедура существенно отличается от процедур, к которым привыкло большинство программистов. В интерфейсе процедуры явно указываются не только тип
данных, но и то, что они – сигналы, а также их направление: входные или выходные данные. При вызове процедуры ей не просто передается управление, а ее копия переписывается в модуль, который ее вызывает и там она связывается. Выполнение этой процедуры запускается по фронту синхросигнала CLK в операторе wait и останавливается после выполнения ее последнего оператора.
В данной процедуре при каждом ее запуске при EDIN = ‘1’ в массив RAM по счетчику datact записывается очередная пара данных.
Процедура SCATTER_C выглядит следующим образом.
procedure SCATTER_C(signal CLK,START,EDIN:in std_logic;
pt:natural; --масштаб результата
signal RAM:in MEMOC; --входной массив
signal datact: inout natural; --счетчик данных
signal rdy: out std_logic; -- конец вывода массива
signal DR,DI: out integer ) -- выходные данные
is
variable s:real:=real(2**pt); -- масштабный коэффициент
begin
wait until CLK='1';
if START='1' then
datact<=RAM'left;
elsif EDIN='1' then
RDY<='0';
DR<= integer(RAM2(datact).RE/s);
DI<= integer(RAM2(datact).IM/s);
if datact< RAM'right then
datact<=datact+1;
end if;
if datact=RAM'right-1 then
RDY<='1';
end if;
end if;
end procedure;
Эта процедура работает так же, как и предыдущая. Но наоборот, накопленные в массиве данные последовательно выдаются на ее выход (gather – собирать, scatter – разбрасывать).
Наконец, процедура, вычисляющая БПФ массива данных выглядит так:
procedure FFT(N:positive; -- размер преобразования =2**N
signal rdy:in std_logic; -- запуск преобразования
signal RAM_I: in MEMOC; -- входной массив данных
signal RAM_O:out MEMOC) -- выходной массив спектров
is
constant NN:positive:=2**N;
variable TWIDDLE:MEMOC_2; -- массив вращающих коэффициентов
variable RAM:MEMOC; -- рабочий массив
variable a,b,c,d,w: complex;
variable al:real;
variable base,itera,datact,twiddlect,twiddleinc: natural;
variable delta:integer:=1;
variable addrf: std_LOGIC_VECTOR(N-1 downto 0);
variable addri: std_LOGIC_VECTOR(N-1 downto 0);
begin
-- формирование таблицы вращающих коэффициентов
for i in 0 to NN/2-1 loop
al:= (MATH_PI*real(2*i))/real(NN);
if IDCT=0 then
TWIDDLE(i):=(COS(al),-SIN(al)); -- для прямого БПФ
else
TWIDDLE(i):=(COS(al), SIN(al)); -- для обратного БПФ
end if;
end loop;
loop -- основной цикл
wait until RDY='1'; -- начало БПФ
-- двоично-инверсная перестановка входных данных
addrf:=(others=>'0'); -- вектор адреса для прямого порядка
datact:=0;
for i in 1 to NN loop
for ind in 0 to N-1 loop -- инвертирование порядка бит
addri(ind):=addrf(N-1-ind); -- инверсный адрес
end loop;
RAM(CONV_INTEGER(unsigned(addri))):=RAM_I(CONV_INTEGER(unsigned(addrf)));
addrf:=unsigned(addrf)+1;
end loop;
-- собственно БПФ
itera:=0;
delta:=1;
twiddleinc:=0;
for itera in 1 to N loop --начало итерации
base:=0;
twiddlect:=0;
for butterfly in 0 to NN/2 - 1 loop
a:=RAM(base); -- начало базовой операции
base:=base+delta;
b:=RAM(base);
w:=TWIDDLE(twiddlect);
c:=a + b * w; -- собственно бабочка
d:=a - b * w;
RAM(base-delta):=c;
RAM(base):=d; -- конец базовой операции
-- модификация параметров базовой операции
base:= base + delta;
if base >= NN then
base:=base-NN+1;
twiddlect:=twiddlect+twiddleinc;
end if;
end loop; --конец итерации
-- модификация параметров итерации
delta:=delta*2;
if itera=1 then
twiddleinc:=NN/4;
else
twiddleinc:=twiddleinc/2;
end if;
end loop;
RAM_O<=RAM; -- результаты БПФ
end loop;
end procedure;
Здесь выполняется известный алгоритм БПФ по основанию 2 с прореживанием по времени с замещением данных [5]. Процедура имеет два участка: первый из них выполняется однократно в начале моделирования, а второй – собственно БПФ – выполняется периодически. При выполнении первого участка формируется таблица вращающих коэффициентов, размер которой равен длине преобразования и которая затем используется алгоритмом БПФ.
Второй участок представляет собой бесконечный цикл. Цикл запускается, как только готов массив исходных данных, подготавливаемый процедурой GATHER_C. После запуска данные переписываются из входного массива в рабочий массив. При этом выполняется двоичная инверсия адресов записи. Следует отметить простую и оригинальную возможность двоичной инверсии адреса, которую предоставляет язык VHDL. Адрес представляется битовым вектором и биты в нем переставляются в инверсном порядке непосредственно. В обычных языках для этого необходимо выполнить довольно сложный и не всегда очевидный алгоритм.
Как и все алгоритмы БПФ, данный алгоритм представляет собой гнездо циклов. Во
внутреннем цикле выполняются базовые операции БПФ, а внешний цикл образован N итерациями алгоритма БПФ.
Исполнительная часть архитектуры содержит вызовы описанных выше процедур:
begin
INPUT:GATHER_C(CLK,START,EDIN,
DR=>DIN_Re,DI=>DIN_IM,
rdy=>idatardy,datact=>datact_I,RAM=>RAM1);
SPECTRUM:FFT(N,idatardy,RAM_I=>RAM1,RAM_O=>RAM2);
OUTPUT: SCATTER_C(CLK,idatardy,EDIN,PT,
RAM=>RAM2,DATACT=>datact_o,
rdy=>rdy,DR=>DOUT_RE,DI=>DOUT_IM);
DEL:process(CLK) begin
if CLK='1' and CLK'event and EDIN='1' then
READY<=idatardy;
NUM<= datact_o;
end if;
end process;
end FFT_int;
Для понимания исполнения программы следует напомнить, что параллельный вызов процедуры, в которой применяется оператор wait, эквивалентен оператору процесса, тело которого состоит из тела процедуры. Таким образом, все три процедуры, как и эквивалентные им процессы, исполняются параллельно в некотором конвейерном режиме. При этом данные и управление передаются от процедуры к процедуре как между ступенями конвейера. В результате, объект FFTbeh обрабатывает непрерывный поток данных, сегментируя его на блоки длиной 2**N.
Процесс DEL выполняет задержку сигнала готовности READY и потока номеров NUM отсчетов результата на один такт, чтобы они соответствовали выходным отсчетам сигналов DOUT_RE и DOUT_IM .
Рассмотрим простой пример применения объекта FFTbeh для измерения спектра сигнала, выдаваемого генератором прямоугольных импульсов. Графическая программа, подготовленная в среде Aldec Active HDL, показана на рис.1.
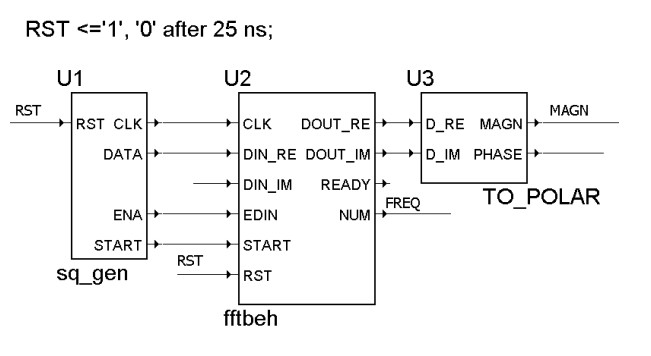
Здесь компонент U1 представляет собой программируемый генератор прямоугольных импульсов DATA с выдачей синхросерии CLK, сигналов START и ENA. Компонент U2 – это описанный выше блок БПФ, а U3 – преобразователь комплексных чисел из прямоугольной системы координат в полярную.
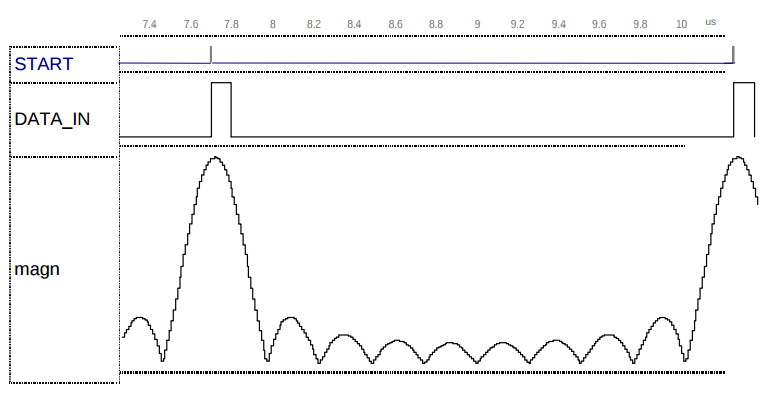
Как указывалось выше, VHDL – симулятор может выдавать на экран целочисленный сигнал в виде графика. Как привило, этот график с осями представлен с помощью средств векторной графики. Поэтому его можно выделить и через “карман” ПК переместить, например, в редактор текста, такой как MS Word. На рис.2. показаны графики сигналов, сгенерировнных при моделировании модели на рис.1. В этом эксперименте определялся спектр прямоугольного импульса с периодом 256 тактов и длительностью 10 тактов с помощью БПФ длиной 256 отсчетов.
Как видим, предложенный блок БПФ эффективен в использовании. Получаемые с помощью его графики спектра удобны как для восприятия, так и для документирования и сохранения. Причем скорость вывода графиков и быстродействие системы при их изучении (перемещение, изменение масштаба, измерение в заданных точках) многократно выше, чем при использовании Matlab’a.
При необходимости, описанный блок БПФ можно без особого труда доработать для того, чтобы входные и выходные данные были с плавающей запятой. Такая доработка сводится лишь к замене целого типа данных на тип real.
Заключение
VHDL – это язык с широкими возможностями. Но, к сожалению, в большинстве случаев он используется лишь с целью описания и моделирования схем на уровне вентилей и регистровых передач. Его традиционные пользователи для других целей используют языки С, С++, системы Delphi и Matlab. В данной статье показаны такие возможности VHDL, применение которых позволяет отказаться от Matlab’а, по крайней мере, при решении задач обработки сигналов. В частности, VHDL-симулятор обыгрывает Matlab и другие подобные системы при моделировании алгоритмов обработки сигналов с целыми числами.
Для эффективного использования VHDL-симуляторов необходимо разрабатывать пользовательские пакеты процедур и функций, аналогичных таким, которые применяются в Matlab’e, а также эффективные средства для представления одно- и двумерных сигналов в графическом виде.
Как посткриптум, следует сообщить, что в последних версиях симулятора Active HDL встроены средства для создания и моделирования поведенческих моделей в формате Matlab’a и подключения их к системе Matlab, при одновременной работе обеих систем [6]. Т.е. VHDL–симулятор выполняет скоростное моделирование сложных блоков Simulink – программ, а Matlab параллельно с Active HDL моделирует остальные блоки и отображает результаты моделирования. При этом обеспечивается работа с целыми числами любой разрядности вплоть до 56. Также возможна трансляция VHDL – моделей в М – файлы для Matlab’a. Этим самым достигнуты компромисс в конкуренции и/или договоренность о кооперации между Matlab и VHDL.
Литература.
1. http://matlab.exponenta.ru
2. Сергиенко А.М., Клименко А.И., Шевченко Ю.А.. Овраменко С.Г. Конфигурируемая вычислительная система для решения задач линейной алгебры. Электронное моделирование. – Т.27. – №1. – с.50-55.
3. Kanevski J., Guzinski G., Pawlowski P., Maslennikov O. Current-Mode Binary and Ternary Elements. Труды Межд. Симп. Компьютеры в Европе. -Киев: -1998. –с.203-212.
4. http://www.vhdl-ams.org
5. Рабинер Л., Гоулд Р. Теория и применение цифровой обработки сигналов. –М.: Мир.–1978. –848 с.
6. Aldec’s New Co-Simulation Wizard for Simulink Offers Support for Mixed HDL/System Design. October 22, 2003. http://www.aldec.com