Square root calculations in FPGA

Sergiyenko A. M.,  Hasan M. J.,  Sergiyenko P. A.
Computer Engineering Department of NTUU “Igor Sikorsky Kyiv Polytechnic Institute”, Kyiv, Ukraine

Introduction. The square root function √x is important elementary function in the scientific calculations, digital signal and image processing [1]. The artificial neural nets need this function √x as well [2]. At present, the field programmable gate arrays (FPGAs) are expanded for solving the problems,  where the function √x calculations are of demand. There are different IP cores of the function √x, which are proposed by the FPGA manufacturers and third-party companies [3]. But these IP cores were designed decades ago and they usually don’t take into account the features of the new FPGA generations.
Therefore, they need improvements. In the presentation, an improved algorithm of the function √x is proposed, which is suitable for the FPGA implementation.

CORDIC-type algorithms. The CORDIC-type algorithm of the elementary function calculation derives a single exact digit of the result in each computation step. The well-known CORDIC algorithm of the √x calculations consists in the following. It calculates the function atanh(x/y). But the side result  is the function K √︀(x² – y²), and by the substitution x = A + 0.25, y = A − 0.25, we get x _n = K √︀A [3]. The disadvantages of this algorithm are additional multiplication to the coefficient 1/K ≈1.207, and repeating some iterations for the algorithm convergence.

More constructive algorithm is the CORDIC-like algorithm of the function √x calculation [4], which is based on the following relations. For each number x ∈ [0.25; 1.0] the coefficients a _i ∈ [0; 1] are found so

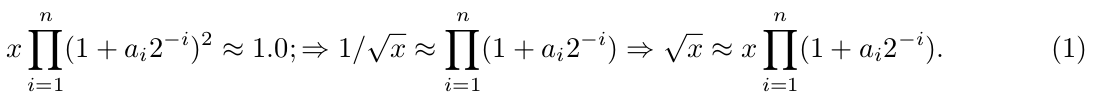
The algorithm is the following:

x[0] = x; y[0] = x;
for(i = 0, i < n, i++) {t = x[i] + 2^(-i)x[i];
	q = t + 2^(-i)t;
	if (q < 1) {x[i+1] = q; y[i+1] = y[i] + 2^(-i)y[i];}// a[i]=1
	else {x[i+1] = x[i]; y[i+1] = y[i];}// a[i]=0
}

The result is √x ≈ y[n].

Modernized algorithm. The most delay in the considered algorithm gives the twofold addition of the shifted data.These stages of addition can be substituted by a single stage:

q = (x _i + 2 ⁻ⁱ x _i ) + 2 ⁻ⁱ (x _i + 2 ⁻ⁱ x _i ) = x _i + 2 ⁻ⁱ⁺¹ x _i + 2 ⁻²ⁱ x _i .

Because modern FPGAs perform the three input adder as a single stage of the six input look- up tables (LUTs), then such computations can be implemented for a single clock cycle without additional time and hardware overheads.
The algorithm analysis shows that when i reaches the limit n/2, then the most i–1 significant bits of x _i become equal to a one by any x ₀, and i most significant bits of y _i are exact digits of the result.
Therefore, the rest of resulting bits can be calculated after analysis and computation the difference 1–x _i.
Consider ε₁ = 1–x_n/2 , and √x = ε_x + y_n/2 . Then, to get the exact result, the correction ε_x is derived from the value ε₁ , and it is added to the approximated result. Due to (1),

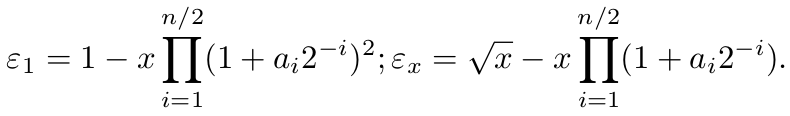
Then

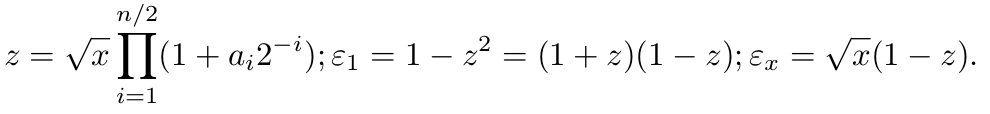
Consider z ≈ 1, then ε₁ ≈ 2(1 − z); ε _x ≈ (√x ε₁ )/2 = y_n/2 (1–x_n/2 )/2. The result is y_n = y_n/2 + y_n/2 (1 − x_n/2 )/2. So, in order to obtain a refined result, the correction is added to the approximate result y_n/2 . To do this, a subtraction and a multiplication should be taken. Moreover, due to the fact that ε₁ and ε_x have the zeroed most significant bits, then the multiplication is performed at half bit width. The resulting algorithm looks like the following:

x[0] = x; y[0] = x;
for (i = 0; i < n/2; i++) {
	q = xi + 2^(-i+1)x[i] + 2^(-2i)x[i];
	if (q < 1.0) {x[i+1] = q; y[i+1] = y[i] + 2^[-i]*y[i]; }
	else {x[i+1] = x[i]; y[i+1] = y[i];}
}
y = y[n/2] + y[n/2](1.0 - x[n/2])/2;

In modern FPGA the two and three input adders have the same hardware volume and speed. So, the modified algorithm provides the speed-up approximately in four times comparing to the initial algorithm.

Experimental results. The derived algorithm was described by VHDL as the IP core. It was compiled for Xilinx Spartan-6 FPGA for various input and output data bit widths. Fig. 1 and Fig.2 show the relation of the hardware costs in the number of LUTs, and the maximum clock frequency on the bit width for the combinatorial and pipelined networks of this IP core, respectively. It should be noted that the modules with a bit width up to 32 additionally have a single multiplication block DSP48, and the rest of them have four such blocks.

For comparison, Fig. 1, 2 show the characteristics of the IP cores offered by Xilinx Inc. In general, the proposed IP core loses to the branded one. But its advantages are that it is free and it can be configured for arbitrary input and output bit width, and for any FPGA type. In addition, the proposed IP core has a lower latent delay.

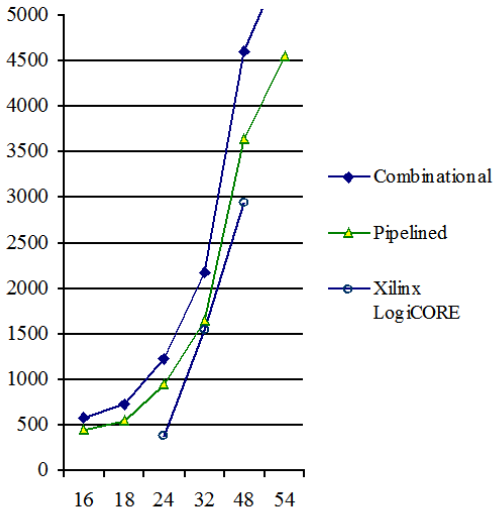
Figure 1. Hardware volume of the √x IP core

For example, for 24 bits, its latent delay is only 15 cycles versus 24 cycles of the competitor. This means that when implementing the floating-point calculations, the proposed module provides greater performance.

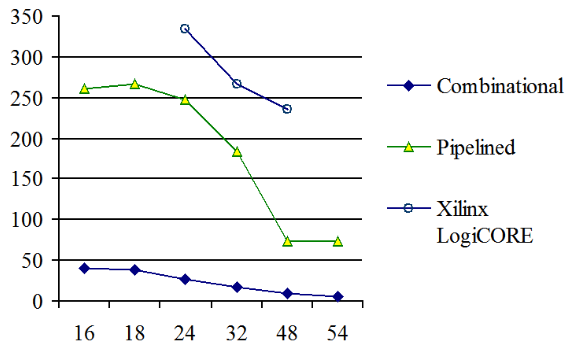
Figure 2. Clock frequency, MHz, of the √x IP core depending on the bit width

Conclusion. The modified CORDIC-like algorithm for deriving the square root function is proposed. The algorithm is distinguished by the minimized number of steps, which is proportional to the given data and result bit width. The algorithm is described in VHDL and is intended for the FPGA implementation. It is the most effective during its implementation in the floating point square root module.

References.

1. R. Woods, J. McAllister, G. Lightbody, and Y. Yi “FPGA-based Implementation of Signal Processing Systems”J. Wiley and Sons, Ltd., Pub. 2008. 364 p.
2. “FPGA Implementations of Neural Networks”. A. R. Omondi, and J. C. Rajapakse, Eds. Springer. 2006. 360 p.
3. K. Yoshikawaa, N. Iwanagaa, and A.Yamawaki “Development of Fixed-point Square Root Operation for High-level Synthesis”. Proc. 2nd Int. Conf. on Industrial Application Engineering. 2014. pp. 16-20
4. T.C. Chen “Automatic computations of exponentials, logarithms, ratios and square roots”. IBM J. Res. and Develop. 1972. No4. pp. 380-388.