High Speed AR Analysis Based on FPGA
Зб.праць 10 Всеукраїнської міжнарод. конф. з оброблення сигналів і зображень та розпізнавання образів — УкрОбраз’2010. − Київ: ІК ім Глушкова. − С.173-176.
High Speed AR Analysis Based on FPGA
Аnatolij Sergiyenko, Dmitry Ivanov, Juriy Vinogradov, Tatyana Lesyk
Department of Computer Engineering
National Technical University of Ukraine “KPI”
aser@comsys.kpi.ua, http://kanyevsky.kpi.ua
Abstract
Two structures of the processors for the autoregressive analysis are considered. The first of them implements the Durbin algorithm using the rational fraction calculations. The second of them implements the adaptive lattice filter. The processors give the possibility of the signal analysis with the sampling frequency up to 300 MHz being configured in FPGA. The processors can be effectively used for adaptive filtering and pattern analysis in the ultrasonic installations, radars, software defined radio, etc.
1. Introduction
Autoregressive (AR) analysis is an effective approach for the estimation of the complex physical object parameters. Besides, these objects can be modeled on the base of their AR analysis. Therefore, the AR analysis is widely used in the economics, geophysics, medical diagnostics, mobile phones, voice recognition, etc.
The use of the field programmable gate arrays (FPGAs) gives the opportunity to analyze the signals in the range of up to hundreds of megahertz. The most of FPGA applications use the fixed point calculations, which maximizes their speed and minimizes the hardware volume. But the AR analysis algorithms afford the increased calculation precision, and they mostly use the floating point data representation.
The AR analysis is based on the assumption that the object can be represented by the AR filter. This filter makes filtering of some excitation signal, in general, of random ones, and derives the analyzed digital signal x(n). In some situations, like in the vocoders, the excitation signal has some predefined form. The AR filter coefficients, named as the prediction coefficients ai (i=0,…,p), are found in two steps. On the first step, the autocorrelation function samples rxx(i) of the signal x(n) are estimated. On the second step the normal Yule-Walker equation system is solved, like the following:
Rxx (a1 ,…, ар )Т = – (rxx (1),…,rxx (p))Т , (1)
where Rxx is the symmetrical Toeplitz matrix, which first row is equal to rxx(0),…,rxx(p − 1), а0 =1 [1].
Equation system (1) is usually solved using the Durbin algorithm, which can be represented by the following loop nest
for i = 1 to p
a0 = 1;
ki = – (a0 * ri +...+ ai−1 * ri )/Ei−1 ;
ai = ki ;
for j = 1 to i−1
aj = aj + ki * ai−j;
end
Ei=(1 − ki2) * Ei−1 ;
end;
(2)
where the initial value of the error prediction is E0 = rxx(0) = r0. Both prediction coefficients ai and reflection coefficients ki are used as the AR analysis results.
The coefficients ai are used in the methods of the high resolution spectrum analysis. The distance between coefficients ki, which values approach to ±1, is interpreted as the distance between physical medium layers, where the excitation signal is reflected. Either coefficients ki, or the roots of the polynomial given by the coefficients ai are used as the voice parameters in the modern vocoders. Both coefficient sets are often used as the initial data for the pattern recognition. This shows the importance of the AR analysis at the field of the pattern recognition.
The analysis of the algorithm (2) shows that its operation number is of the order of p2 , and its parallelizing is severe. Therefore, more complex, but well parallelizable algorithms like QR-factorization algorithm are often recommended to solve the equation (1) [2,3]. For this purpose, the Givens algorithm or the Toeplitz matrix inversion algorithm can have a success by their FPGA implementation [4].
Consider the coefficient Ei approaches to zero in the algorithm (2). Then the division to Ei can force the result ki to be much higher than 1.0. Another words, this algorithm is very sensitive to the calculation errors. This is the cause that the system equation solving affords the calculations with the increased precision. Analogous properties have the similar algorithms of the Toeplits equation solving [2]. Therefore, the AR analysis problem is usually solved using the floating point microprocessors.
In the presentation the structures of the application specific processors are proposed, which are configured in FPGA, and which implement the AR analysis in the wide frequency range using the fixed point calculations.
2. AR processor based on the Durbin algorithm
To derive the stable estimations of ai, the values rxx(i) must be accumulated for at least qp = 10р samples of data [1]. When р is limited by tenths, then the correlation function rxx(i) complexity is approximately in рtimes higher than equation system (1) solving complexity. When as usual, the input data are sampled in sequence, then the time of the AR analysis is equal at least qp clock cycles. As a result, the correlation function rxx(i) accumulation is predominant in the time balance of the whole AR analysis.
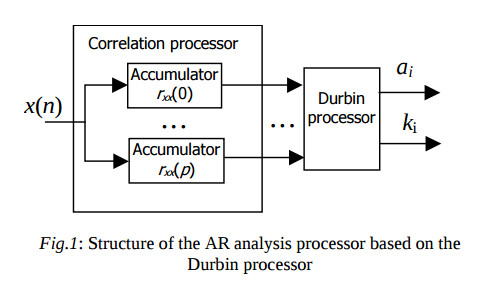
Consider the structure of the AR processor, which consists of the correlation processor and the parallel processor array for the equation (1) solving. Then, the equation system solving using this parallel processor array could not give the valuable throughputincrease comparing to the usual sequential solver. In this situation the processor structure for the AR analysis is proposed, which contains correlation processor and Durbin algorithm processor.
The correlation processor is the linear array of р processor units, which are operating with the fixed point data. The Durbin algorithm processor implements the calculations with the increased precision. This structure is illustrated by the fig.1. Both processors implement their tasks approximately for the equal period of time in the pipelined manner.
The critical path in the algorithm (2) approaches through the cyclic path of multiplier and adder in the coefficient ki calculation. By the pipelined implementation of the arithmetical operations the iteration period is no less than the stage number of the adder and multiplier pipelines. If the floating point arithmetical units are used then the iteration period is no less than 7 clock cycles, and the unit is underloaded [5].
In [6] the rational fraction arithmetic operations were proposed for the linear algebra problem solving, which provide the advantages by the FPGA implementation. The rational fraction number x is represented by two integers, one of them is a numerator nx , and another one is a denominator dx, i.e. x = nx/dx. All the data are represented by these fractions.
Then multiplication, division, and addition are calculated by the formulas:
x − y = nx ⋅ ny /(dx ⋅ dy );
x/y = nx ⋅ dy /(dx ⋅ ny );
x + y = (nx ⋅ dy + ny ⋅ dx )/(dx ⋅ dy).
Such calculations are supported in the modern FPGA by a set of hundreds of multiplication and accumulation units like DSP48 unit in Xilinx Virtex FPGAs. The use of rational fraction calculations provides both small error level and expanded dynamic range, as well as the high speed and simple implementation in FPGA. The mentioned above iteration period is minimized to 4 clock cycles. Besides, division operation, which is included in the algorithm critical path, lasts very shortly, and adds minimum error to the calculations [7].
If the natural representation of the results is needed then the computations are finished by the division of numerators to denominators of the results ai or ki by the usual division operation. Such a division slightly increases the Durbin processor operation time.
3. AR processor based on the lattice filter
FIR-filter with the coefficients ai is the reverse one to the AR filter. Therefore, the adaptive FIR-filter is often used to derive
the autoregressive coefficients [1,8]. But the slow adaptation of such filters prevents their use for the high speed physical process analysis.
The lattice form of the adaptive FIR-filter is well known, which implements the calculations [1]:
Ejf(n) = Ej-1f(n) + kj Ej-1b(n − 1);
Ejb(n) = Ej-1b(n − 1) + kj Ej-1f(n),
where Ejf(n), Ej-1b(n) are forward and backward prediction errors in the n-th algorithm stage, respectively, kj is the reflection coefficient, E0f(n) = E0b(n) = x(n), j=1,…,p. In the FIR-filters with the sequential adaptation process the coefficients kj are calculated using some recursive gradient algorithm, which converges in several hundreds of steps. In the lattice filter which computes N = qp data samples these coefficients are calculated rather precisely by the following formula for N steps [1]:
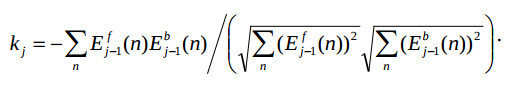
Here the sums in numerator and denominator are the partial correlation coefficients. In this computational schema the coefficients kj are found step by step, beginning at k1 . By this process one input data array is inputted р times to the lattice filter. If the signal is stationary one in the time window of pN samples, then the data stream can be fed into the filter permanently without the input buffer.
The processor for the AR analysis consists of the lattice filter and the coefficient kj calculation unit (see fig.2). At the j-th step of adaptation the coefficient calculation unit is attached to the inputs of the j-th filter stage. It accumulates the partial correlation coefficients for N input data, and calculates the coefficient kj. This coefficient is loaded into the multiplicaton units of the j-th filter stage. As we see, the step of the correlation function estimation and the step of the reflection coefficient finding are combined in this computational schema.
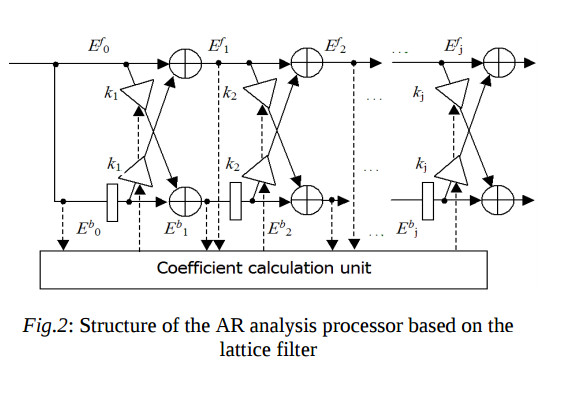
Comparing to the usual adaptive filters, here the robust convergence to the result is achieved only for pN clock cycles. Comparing to the considered above Yule-Walker equation solver, in the lattice filter the computation error accumulation is minimized, and always the stable results occur. Note that the stable results mean that |kj| < 1. Therefore, to implement the coefficient calculation unit the integer number arithmetic is enough.
Such an AR analysis processor can be configured in FPGA, but the integers have to be at least of doubled bit width. The convergence speed can be increased attaching the coefficient calculation units to all the filter stages. But then the hardware volume increases substantially.
4. AR processors implemented in FPGA
Two mentioned above schemes for the AR analysis were carried out in the application specific processors, which are configured in the Xilinx FPGA. The Durbin algorithm processor is based on the arithmetic unit, which implements multiplication, division, accumulation of the rational fractions as well as transformation them in integers. The fraction contains 18-bit numerator and 18-bit denominator. Multiplication and division operations are implemented in the pipelined mode with the period of a single clock cycle with the latent delay of 7 clock cycles. Accumulation operation period lasts 4 clock cycles because this operation result is fed to its input.
The results of the processor implementation for 16-bit data, N = 10 and different values of p are represented in the table 1. Their comparison shows that processors based on the Durbin algorithm have higher clock frequency, less hardware volume and shorter adaptation period. The processor analysis shows, that input data frequency can be increased more than in two times if the correlation processor clock signal is increased [10].
Table 1: Processors of the order р implemented in Xilinx XC4VSX35-12 FPGA
| Processor based on | Hardware volume, CLB slices + DSP48 | Max. clock frequency, MHz | Period of calculating k1,…,kр | |||
|---|---|---|---|---|---|---|
| р = 10 | р =90 | р =10 | р =90 | р =10 | р =90 | |
| Durbin algorithm | 1330 + 16 | 4753 + 96 | 154 | 150 | 610 | 5490 |
| lattice filter | 1446 + 24 | 6822 + 184 | 151 | 145 | 1650 | 86850 |
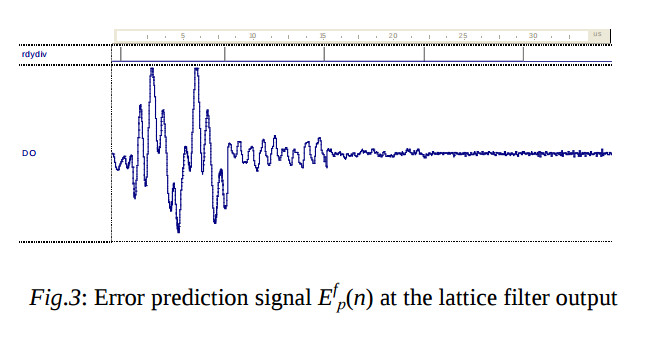
The diagram on the fig.3 shows the prediction error of the lattice filter by the analysis of the white noise, which was filtered by the 6-th order IIR band pass filter. The square impulses show the periods of the coefficient kj calculation. One can see the high speed of the convergence of the adaptation. The processor based on the lattice filter has the advantage for small parameters р and for N < 10, as well as for processing the continuous data flows. Besides, it provides the robust estimation of kj for any input data.
Comparing to the similar processors for the AR analysis based on FPGA [11,12] the proposed processors have substantially less hardware volume. The filter described in [12] has in 20 times more logic cells than the processor based on the Durbin algorithm having the equal multiplier unit number.
5. Conclusions
In the presentation two structures of the processors for the AR analysis are proposed, which give the possibility of the signal analysis with the sampling frequency up to 300 MHz being configured in FPGA. These processors give the possibility to expand substantially the area of the AR analysis use, for example in the ultrasonic devices, wireless communications. The proposed rational fraction number system has the advantages that it provides higher precision than integers do, and is simpler in its implementation than the floating point numbers have.
6. References
[1] Candy J.V., Model-Based Signal Processing, Wiley, Hoboken, New Jersey , 2006, 677p.
[2] Brent R.P., “Old and new algorithms for Toeplitz systems”, Proc.SPIE, Vol.975, Advanced Algorithms and Architectures for Signal Processing III, SPIE,
Bellingham, Washington, 1989, 2–9.
[3] Bojanchuk A.W., Brent R.P. de Hoog F.R., “Linearly Connected Arrays for Toeplitz Least-Squares Problems”, J. of Parallel and Distributed Computing, No9, 1990, 261−270.
[4] Sergiyenko A., Maslennikow O., “Implementation of Givens QR Decomposition in FPGA”, R.Wyrzykowski et al. (Eds.):Proc. PPAM 2001, Springer, LNCS, Vol.2328, (2002), 453−459.
[5] Karlström P., Ehliar A., Liu D., “High performance, low latency FPGA based floating point adder and multiplier units in a Virtex4”, 24th IEEE Norchip Conf., Linköping, Sweden, Nov. 20−21, 2006, 31−34.
[6] Sergyienko A., Maslennikow O., Lepekha V., “FPGA Implementation of the Conjugate Gradient Method”,Proc. PPAM 2005, Springer, LNCS, 2006, Vol.3911, 526-533.
[7] Сергиенко А.М. “Применение рациональных дробей в специализированных вычислителях” Вісник НТУУ «КПІ», сер. Інформатика, управління та обчислювальна техніка, Т.50, 2009, 74-77.
[8] Widrow B., Stearns S.D., Adaptive Signal Processing, Englewod Clifs NJ, Prentice-Hall, 1985. [9] Pohl Z., Matoušek R., Kadlec J., Tichý M., Lícko M.,
“Lattice adaptive filter implementation for FPGA”, Proc. 2003 ACM/SIGDA 11-th Int. Symp., Monterey, California, USA, 2003, 246−250.
[10] Сергиенко А.М. “Спецпроцессоры для авторегрессионного анализа сигналов”, Электрон. Моделирование, 2010, Т.32, No2, с.87-96.
[11] Hwang Y.T., Han J.C. “A novel FPGA design of a high throughput rate adaptive prediction error filter”, 1-st IEEE Asia Pacific Conf. on ASICs, AP − ASIC’99, 1999, 202–205.
[12] Lin A.Y., Gugel K.S., “Feasibility of fixed-point transversal adaptive filters in FPGA devices with embedded DSP blocks”, 3rd IEEE IWSOC’03, 2003, 157-160.