Апаратне моделювання поширення ультразвукових хвиль у твердому тілі

УДК 004.942

Анатолій Сергієнко, Мустафа Рекар Касім

Anatoliy Sergiyenko, Mustafa Rekar Quasim.   Modeling the ultrasound wave propagation in the solid BODY by the hardware

Розглянуто удосконалений хвилевий алгоритм моделювання поширення ультразвуку, який полягає у представленні середовища у вигляді системи хвилевих фільтрів та відрізняється тим, що завдяки реалізації багатоканальних фільтрів з програмованою затримкою, зменшується похибка моделювання дисперсійного поширення звуку. Алгоритм при реалізації у ПЛІС дає змогу виконувати моделювання у реальному часі.
Ключові слова: ПЛІС, дисперсія звуку, хвилевий фільтр.

The improved ultrasound propagation wave modeling algorithm is proposed, which consists in representing the medium in the form of a system of the wave digital filters. The algorithm differs in that due to the implementation of the multichannel filters with the programmable delays, the simulation error of the sound propagation dispersion is decreased. The algorithm implementing in FPGA provides the modeling in real time.
Key words: FPGA, sound dispersion, wave digital filter.

Вступ. Акустичні процеси в твердих тілах зазвичай моделюються в комп’ютерах за допомогою методу різницевих рівнянь, який вимагає великих обчислювальних ресурсів [1]. Для мінімізації цих ресурсів часто використо­вують метод цифрових хвилеводів, або метод DWG (digital waveguide), який забезпечує високошвидкісні обчислення [2]. Багато успішних прикладів впровадження методу DWG показано в моделюванні та звуковому синтезі струнних, духових та віртуальних музичних інструментів, а також в вокодерах [2, 3, 4]. Але ця модель не враховує розсіювання (дисперсію) хвиль у поширенні звуку.

У даній роботі пропонується модифікація методу DWG, яка забезпечує моделювання звукової дисперсії в твердій смужці.

Основи моделі DWG. DWG – це цифрова модель розповсюдження хвиль в ідеальному хвилеводі. Вона базується на принципах, описаних у роботі [5], але адаптованих до моделювання звукових хвиль [2,4]. При цьому у i-й точці хвилеводу розглядаються прямі f_i = Rv_f і зворотні хвилі b_i = –Rv_b, де f_i та b_i – це тиск прямих і зворотних (віддзеркалених) хвиль, відповідно R – хвилевий імпеданс, v_f, v_b – швидкості частинок речовини. Для жорсткого циліндра з площею перетину A цей імпеданс дорівнює R = ρc_оA, де ρ – густина матералу, c_о– швидкість поздовжних хвиль. Реальне значення тиску дорівнює сумі тисків прямої та зворотної хвиль: u = f_i + b_i.

У цифровій моделі DWG сигнали квантуються з частотою дискретизації F_s, яка, щонайменше, в два рази перевищує максимальну частоту хвиль, які досліджуються. Тоді i-й сегмент хвилеводу довжиною L виглядає як дві лінії затримки на n = L/(c_oF_s) тактів сигналу дискретизації.

Кілька однорідних хвилеводів з’єднануються між собою в одній точці за допомогою вузла адаптера, який також називають вузлом розсіювання. Функціонування адаптера повинне підлягати закону Кірхгофа. Для випадку з’єднання двох хвилеводів це означає виконання рівнянь:

v_b1 = rv_f1 + (1 – r)v_f2;                       (1)

v_b2 = (1 + r) v_f1 – rv_f2;

де r = (R₂ – R₁)/(R₂ + R₁) – коефіцієнт віддзеркалювання. Так само, коли підклю­чено три хвилеводи, то у вузлі адаптера розраховуються наступні формули:

v_b1 = (2g₁ – 1) v_f1 + 2g₂ v_f2 + 2g₃ v_f3;

v_b2 = 2g₁ v_f1 + (2g₂ – 1) v_f2 + 2g₃ v_f3;                   (2)

v_b3 = 2g₁ v_f1 + 2g₂ v_f2 + (2g₃ – 1) v_f3;

 де v_f1, v_f2, v_f3 – хвилі, що входять у вузол, v_b1, v_b2, v_b3, – хвилі, що виходять з вузла, g₁, g₂, g₃ – питомі імпеданси хвилеводів, такі що g₁ + g₂ + g₃ = 1, та g_i = R_i/(R₁ + R₂ + R₃), i = 1, 2, 3.

Удосконалена модель DWG. Згідно з теорією поширення акустичних хвиль у твердих тілах, які мають обмежені розміри, наприклад, у стрижнях, розглядають основні – повздовжні хвилі з фазовою швидкістю c_p та вторинні – поперечні хвилі зі швидкістю c_s, причому c_s < c_р [6]. При взаємодії цих хвиль вони можуть перетворюватись одна в іншу. Це можна промоделювати при з’єднанні хвилеводів з такими хвилями у вузлі адаптера.

Крім того, повздовжні хвилі мають дисперсію, тобто, їх швидкість c_pзалежить від довжини хвилі λ. Наприклад, швидкість повздовжних хвиль у циліндрі оцінюється формулою [6]:

c_р = c_о(1 – ν²p²a²/ λ²) = f(λ),               (3)

де ν – коефіцієнт Пуассона, що дорівнює 0,29 для сталі, a – радіус циліндра. Тому модель DWG повинна бути зкоректована ​​відповідно до цієї формули.

Модифіковану модель DWG деякого стрижня або циліндра можна предста­вити структурою, яка показана на рис.1. Ця модель складається з лівого (LА) та правого (RА) адаптерів, хвилепроводу P продольних хвиль та хвилеводу S поперечних хвиль. У кожному з трьохпортових адаптерів обчислюються вирази (2). Їхні порти, які означають торці стрижня, підключені до мереж, які реалізують віддзеркалення хвиль з коефіцієнтом придушення s_L та s_R згідно з рівняннями (1). Сигнал збудження v_in подається у модель через суматор.

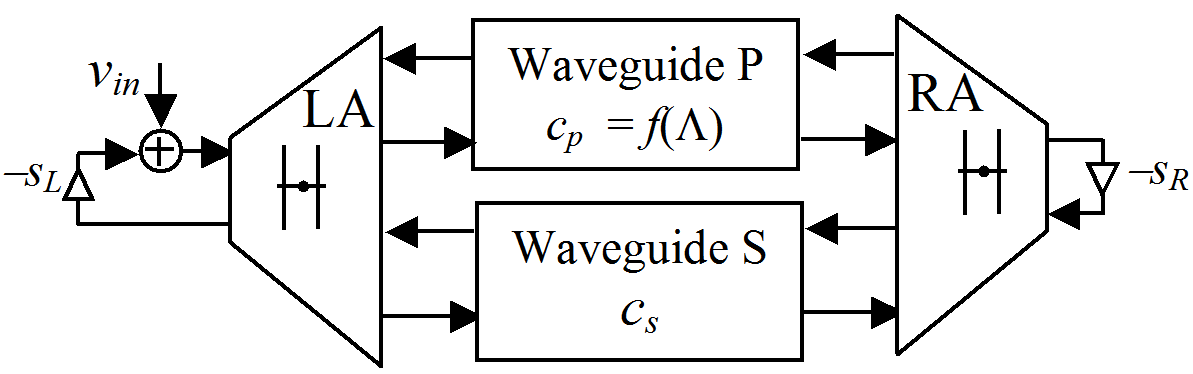
Хвилевід S виконує затримку на задану кількість тактів частоти дискретизації та певне ослаблення хвилевого сигналу. Хвилевід Р складається з кількох каналів, кожен з яких має окремі діапазон частот пропускання, затримку і згасання в залежності від відповідної довжини хвилі λ згідно з (3).

Отже, модифікована модель DWG здатна приймати до уваги дисперсність поширення звуку у твердому тілі, тобто, залежність фазової швидкості звуку від його довжини хвилі або частоти.

Експериментальні результати. Була розроблена програмна модель стрижня зі структурою як на рис. 1. В ній до восьми каналів хвилеводу P реалізуються на основі смугових фільтрів на базі фазового хвилевого фільтра, який описано у [7]. Кожен канал хвилеводу має динамічно настроюваний смуговий фільтр, який реалізовано так, як показано в [8]. Сумарна амплітудно-частотна характерис­тика хвилеводу S показана на рис.2. Тут частота f вимірюється в частках частоти дискретизації Fs. На рис.2 також показані частотні характеристики двох сусідніх каналів хвилеводу.

Модель збуджувалась вузьким ультразвуковим імпульсом, а інтенсивниість звуку v вимірювалась на виході вузла суматора (див. рис.1). Часова діаграма, яка представляє хвильовий сигнал, показана на рис.3. Ця діаграма показує, що хвилі дійсно зазанають дисперсії під час розповсюдження через модель стрижня.

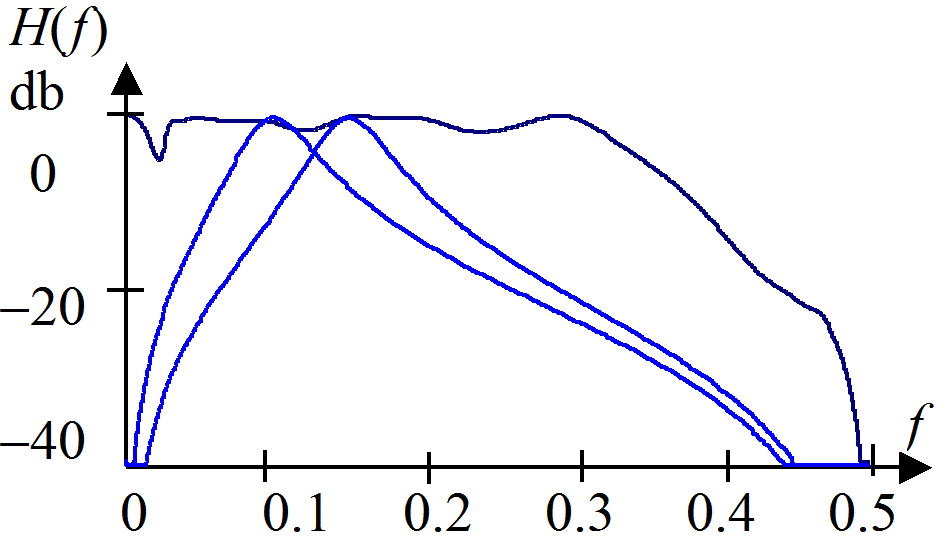
Рис. 2. Сумарна амплітудо-частотна характеристика хвилеводу Р

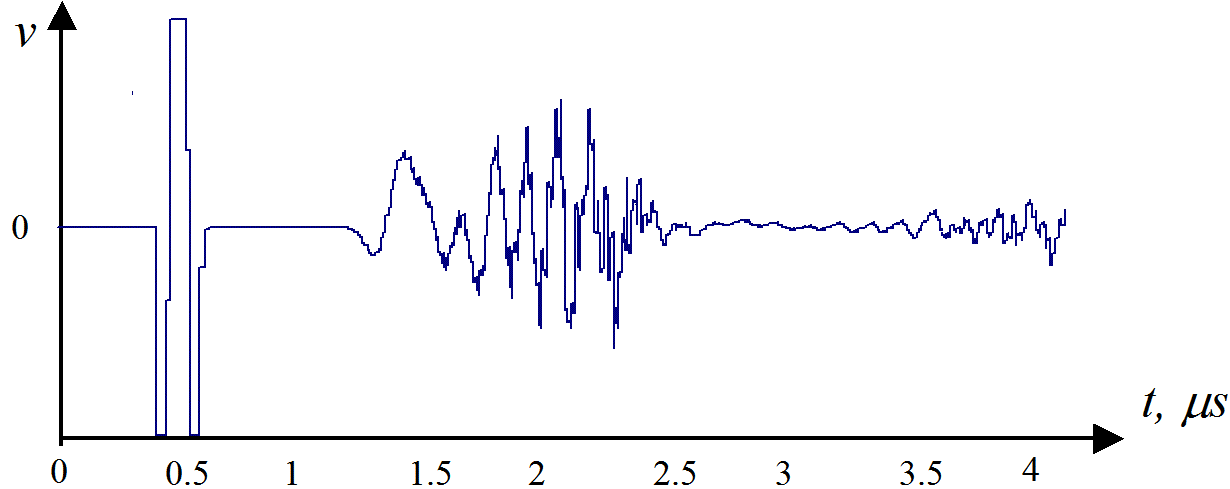
Рис. 3. Часова діаграма поширення ультразвукового імпульсу у стрижні

Модель стрижня описана мовою VHDL, і тому вона може бути реалізована як у симуляторі VHDL, так і в ПЛІС. Модель, описана стилем для синтезу і при конфігуруванні у ПЛІС Xilinx Spartan-6, містить 2680 логічних елементів, 60 блоків множення DSP48, та 16 блоків пам’яті BlockRAM. При цьому забезпечується частоту дискретизації сигналу F_s < 100 МГц. Така частота забезпечує моделювання в режимі реального часу.

Висновки. Запропоновано модифікований метод DWG для моделювання твердого тіла, який враховує дисперсність поширення хвиль. Метод заснований на моделі цифрового хвилеводу, затримка якого залежить від довжини хвилі. Приклад моделі стрижня, описаної на VHDL, показує ефективність цієї моделі.

Посилання

1. Самарский А.А. Математическое моделирование. Идеи. Методы. Примеры / Михайлов А.П. / М.: Физматлит, 2001. -320 с. 
2. Smith III J. O. Physical Modeling Using Digital Waveguides // Computer Music Journal, V.16. 1993. №4. P.74-91.
3. Karjalainen M. Digital Waveguides versus Finite Difference Structures: Equivalence and Mixed Modeling / C. Erkut // EURASIP Journal on Applied Signal Processing 2004. №7. P. 978–989.
4. Маркел Дж. Д. Линейное предсказание речи. – М.: Связь. 1980. 308 с.
5. Fettweis A. Wave digital filters: Theory and practice // Proc. IEEE, V74, 1986. №2. P. 270 – 327.
6. Kolsky H. Stress Waves in Solids. Dover Publications Inc. 2012.
7. Regalia P. A., The Digital All-Pass Filter: A Versatile Signal Processing Building Block / S. K. Mitra, P. P. Vaidyanathan //Proc. IEEE. V.76. 1988. №1. P. 19-37.
8. Сергиенко А. М.,  Лесик Т. М., Перестраиваемые цифровые фильтры на ПЛИС /  // Электронное моделирование, Т.32. 2010, №6. C. 47-56.