Mapping DSP Algorithms into FPGA
Proc. of IEEE East-West Design & Test Symp.,
EWDTS’ 08. —Lviv, October 9-13, 2008. —
Kharkov: KNURE. —2008. —p.325—330.
Mapping DSP Algorithms into FPGA
Oleg Maslennikow Polytechnica Koszalinska, Poland, E-mail: oleg@moskit.ie.tu.koszalin.pl
Anatolij Sergiyenko, Tatyana Lesyk National Technical University of Ukraine E-mail: aser@comsys.ntu-kpi.kiev.ua
Abstract Methods of mapping DSP algorithms into FPGA are considered. Algorithms are represented by synchronous data flow graphs, and are mapped into pipelined data paths. The methods consist in placing the algorithm graph in the multidimensional index space and mapping it into structure and event subspaces. The limitations to the mapping process minimize both clock period and hardware volume including multiplexor inputs.
1. Introduction
Modern field programmable gate arrays (FPGAs) having millions of configurable gates and hundreds of hardware multipliers, and operating at hundreds of megahertz clock frequencies are considered to be advanced chips for high speed digital signal processing (DSP). But the design of DSP projects for FPGAs remains the very complex task.
The computing system synthesis usually has three general tasks: resource allocation, operator (actor) scheduling, and binding resources with operators. These tasks consist of subtasks like variable moving scheduling, variable to register or bus assignment, memory allocation, etc. The different synthesis methods are distinguished due to the order and way of such subtask implementation. The operator scheduling is most responsible and complex task. The resulting computing system effectiveness depends on all synthesis task implementation. But they are usually implemented separately. The subtasks have the local targets, which are often in disagreement to another subtask targets. Therefore most of synthesis methods do not provide the effective structure solutions.
In the high-level synthesis the DSP algorithm is usually represented by the synchronous data flow graph (SDF). The nodes of SDF, which are named as actors, represent the algorithm operators. Edges represent variable movings between actors with the FIFO buffering. During a single cycle of SDF modeling each actor generates and accepts a variable (token) set, which quantity is stable in each cycle [1],[2].
DSP algorithms have both cyclic and acyclic SDFs. In general, the subgraphs of the cyclic SDF have different computing periods. The multirate DSP system is an example of such a SDF. Therefore, the SDF scheduling is a complex task. Very popular approach consists in the search for the schedule of an algorithm period, considering the acyclic part of SDF. Here the algorithms of list scheduling, force directed scheduling, graph coloring, left edge scheduling are very popular. But these methods cause the bad load balance of processing units (PUs) at the beginning and the end of the cycle. To consider the cyclic nature of SDF the conflict graph or interval graph are analysed additionally [2],[3].
Recently such programming tools like AccelDSP or System Generator are wide spreaded, which help to generate the FPGA configuration of the DSP computing system. Here the initial algorithm is represented by SDF using Matlab Simulink package [4]. But these tools are effective ones only for аcyclic SDF, for example, FIRfilters, or for actors, which represent the complex library components.
In [5],[6] methods for mapping SDF into parallel computing structures are proposed. They are based on placing the graph in the multidimensional index space and mapping them in subspace of structures and subspace of events. Methods of structural design of digital filters described in [7],[8] use this approach as well. This approach provides simultaneous fulfilment of the synthesis tasks and therefore it optimises the structure of computing system much better. In the representation this approach is described in the application of mapping DSP algorithms into FPGAs.
2. Mapping SDF into subspaces of structures and events
The initial data for the design are DSP algorithms, represented by SDF, and cost functions. The SDF with a single sampling frequency i.e. the homogeneous SDF is considered. The multirate SDF is transformed into equivalent homogeneous SDF. The computing system structure consists of a set of PUs, connected to each other according to the structure graph. A single PU consists of ALU of given type (multiplier, adder, etc.) with the result register or FIFO buffer on its output and with the input data multiplexers on its inputs. PU calculates the operation no longer than a single clock cycle. If PU has not a register then the operation is considered to be calculated without a delay. Such a simple PU can be naturally implemented in the FPGA resources including special DSP hardware like DSP48 units in Xilinx Virtex4 devices.
The cost functions are algorithm period interval: QT = LtC, and hardware cost: QS =∑ Сp qpmax, where L is the computation period in clock cycles, tC – clock cycle duration, Сp – hardware cost of PU of p-th type.
Any network component like multiplexor, adder, etc. have approximately distinct FPGA hardware volume measured in equivalent gate number, logic cell number, CLB slices. From this point of view the average cost of a single multiplexor input of Xilinx FPGAs can be estimated as 0,57 of register cost, or adder cost with the equal data widths. For this reason, the 18-input 16-bit width multiplexor has the cost as the 16-bit multiplier unit has. Therefore, the multiplexor input number minimization is very valued in FPGA projects. Besides, this number represents the interconnection complexity.
According to the method, SDF is represented in the three dimensional index space as the algorithm configuration KG = (K,D,A), where K – is the matrix of vectors-nodes Ki, representing algorithm operators, D is the matrix of vectors-edges, representing variable movings between operators, A is the incident matrix of SDF. The coordinates of the node Ki = <ki,si,ti> are equal to the operator type (for example, k=1 is multiplication), PU number si, in which the operator is implemented, and clock cycle ti, when the operator result is stored in the register.
Equivalent structural solutions are represented by equivalent algorithm configurations, which differ in its matrices К and D. The matrix К codes some correct structure solution, and the matrix D can be derived from the equation D = КА. The optimum structural solution finding consists in the search of the маtrix К, which minimizes the given cost criteria. For example, if the genetic optimisation approach is used then the matrix К serves as a genome of the population representative. The following relations and definitions help to find the effective solutions.
The algorithm configuration is correct if there is none couple of equal vectors in the matrix К, i.e.
∀ Ki,Kj (Ki≠ Kj, i≠ j).
The operator schedule is correct if the operators that are mapped in a single PU are implemented in different clock cycles, i.e.
∀ Ki,Kj(ki=kj, si=sj) ⇒ ti¬≡tj mod L.
A modul operation here represents the cyclic nature of SDF modeling. The operators of the same type are mapped in the PUs of the respective type:
Ki,Kj ∈ Kp,q(ki=kj=p, si=sj=q), |Kp,q| ≤ L,
where Kp,q is a set of nodes of p-th type that are mapped into a q-th PU.
If SDF has a cyclic route i then the sum of vectorsedges Dj, belonging to this route, has to be equal to a zero
∑ bi,j Dj = 0,
where bi,j is the not zeroed element of i-th row of the cyclomatic matrix of SDF. Such cyclic routes are inherent to the IIR filters.
SDF can be represented as the conjunction of the аcyclic subgraph, which implements the calculations of a single algorithm period, and a set of edges DВj. The back propagation vector-edge DВj = <0,0,–kL> means the delay which is equal to k periods (iterations) of the algorithm. Because the edge DВj is directed to the opposite direction comparing to others vectors-edges, it is named as a reversed one. In the multidimensional space these edges are parallel to the time axis оt. It represents the interiteration delay to kL clock cycles. The vector DВj is analogous to the delay node Z–k of the signal graph of the DSP algorithm.
An effective algorithm configuration is searched in two steps. On the first step SDF nodes and edges are placed in the three dimensional space as sets of vectors Ki and Dj with respect to all conditions mentioned above. Then the PU number is minimized satisfying the condition |Kp,q|→L. This condition means that the number of nodes, mapped into a single PU, approaches to L.
On the second step the configuration balancing is implemented. During this procedure the acyclic subgraph of SDF (i.e. SDF without reversed edges DВj) is considered, and in each edge the delay nodes are added. These nodes represent a delay, or storing for a single clock cycle, or a register. In the resulting balanced configuration all the edges except reversed edges are equal to Dj=<aj,bj,1> or Dj=<aj,bj,0>. The configuration nodes form columns, and the distance between adjacent columns is equal to one clock cycle.
The balanced configuration is optimised by mutual interchanges of nodes belonging to a single column. By this process, the register and multiplexor number is minimized. The other methods like resynchronisation, left edge scheduling are used as well.
The computing system structure and the resulting schedule are derived by splitting the algorithm configuration KG to the structure configuration KS and event configuration, which have the same incidence matrix А. The vectors of the structure configuration are equal to <ki,si>, i.e. to the type and number of PU, and the vectors of event configuration are equal to <ti>, i.e. to the clock cycle, in which the mapped operator is implemented. In such a way the algorithm configuration is mapped into the structure subspace and into the event subspace.
3. Multiplexor minimization
Consider the method of multiplexor minimizаtion in pipelined computing system which is effective one for FPGA projects. Very often SDFs of DSP algorithms have a set of isomorphic subgraphs. For example, algorithms of complex IIR filters are the chains of the second order stages, FIR filter graphs have equal periodic parts. High speed recursive filter structures are designed composing identical all-pass filter chains [9]. To minimise the multiplexor number in such structures the following theorems are used.
Theorem 1. Consider the balanced algorithm configuration. Then the multiplexor input amount NМi of i-th PU node not exceeds the number of vectors Dі,j that are not equal to each other, and its arrows are incident to the nodes Ki,k, mapped in this PU.
The theorem proving is evident. Such vectors Dі,j represent the variables that are inputted in i-th PU through different multiplexor inputs. The words “not exceeds” mean the instance when the multiplexor has a single input and is not needed at all. In another situation the multiplexor input number is equal to the different vectornode number.
Theorem 2. Consider the balanced algorithm configuration KG which has up to L isomorphic subgraphs, or equivalent subconfigurations KGОі=(KОі,DОі,AO). Then the structure, which is the result of this configuration mapping with the period L, has the minimum multiplexor input number if and only if all the subconfigurations KGОі are mapped into a single structure subconfiguration KSО, and
∀Ki,j∈KОі(Ki,j= <Cj,k,Cj,l, ti,j>); (1)
∀Ki,j∈KОі(arrow of Di,l is incident to Ki,j ⇒ Di,l= <Ck,Cl, 1>, Cl≠0 ). (2)
This means that the structure subgraph is isomorphic to the proper algorithm subgraphs. Figure 1 illustrates mapping the algorithm configuration with the period L=3 to the structure configuration. Bold line represents the multiplexor.
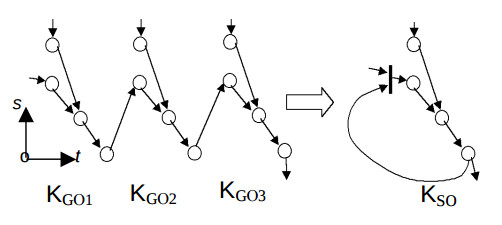
mapping.
The theorem proving. When the conditions (1) and (2) are satisfied then the resulting PU with one input ALU has a single input, and with the two input ALU has two inputs respectively. This means that each PU of resulting subconfiguration has none multiplexor at all, not to consider the inputs of PU (see the Figure 1).
From the opposite side, consider the theorem conditions are satisfied. Let one or two nodes in the subconfigurations exchange their coordinates. Then two situations can be hold on. In the first one, the interchanged node is mapped into additional PU node, which increases the hardware volume. Besides, the vector Di,l, which is outputted from this node, exchanges its coordinates. And in the resulting structure the additional multiplexor input occurs, in which the data is outputted from the additional PU node.
In the second situation the node is mapped into another free PU node, or two nodes are mutually interchanged. Then the two input multiplexers have to be attached to the inputs of this PU, or these PUs. As a result, the conditions (1), (2) are not satisfied by any exchanges in subconfigurations, which cause the increase of PU number or multiplexor input number.
4. Synthesis of digital filters with multiple delays
Usually digital filters are described by the transfer function H0(Z) which depends on the complex variable Z. This function represents the filtering algorithm with the period L=1 precisely. And each multiplicand Z-k in the function represents the delay to k cycles, which can be implemented on the FIFO with k registers. If the register number in each delay FIFO is increased in n times then the filter with the function Hn(z) = H0(Zn) is derived. Such a filter, named the filter with multiple delays, has the following useful property. Its frequency characteristic is similar to the prototype filter characteristic but in the range of 0 to fS these characteristic repeats itself in n times, where fS is the quantisation frequency.
When the filter stages are connected in a chain then the resulting characteristic is the product of the stage characteristics. When these characteristics are different ones then they mask each other. Using the masking effect and multiplied delays of the filter stages, the high quality narrow band filters can be designed, which have small hardware volume [10].
In Xilinx FPGAs the multiplied delays are implemented in FIFO units of SRL16 – type, which occupy the same place as separate registers do. This fact shows that the filter with multiplied delays has the same hardware volume as the usual filter has. For the synthesis of such filters in FPGA the following method is proposed.
On the first step of the method the algorithm is selected which SDF has a set of isomorphic subgraphs. The subgraph edges can be loaded by delays, which are equal to k. Consider the subgraph number is L. This figure provides the maximum hardware utilization but in general, it can have another value. The subgraph with k=1 is represented by the algorithm subconfiguration named as a period configuration. The border nodes in it are selected which are incident to the reversed edges. These border nodes are mapped into iteration inputs and outputs of the structure. The period configuration is optimised as it is mapped into the structure with the parameter L=1, i.e. into the structure with the maximum parallelism.
On the second step up to L subconfigurations and other nodes (if needed) are connected together according the algorithm graph. By this process, the conditions of the theorem 2 must be satisfied. If some filter stages use delays to k cycles then (k-1)L delay nodes are added to reversed edges of their subconfigurations.
On the third step the configuration is mapped into the structure with the period L. The resulting structure consists of the pipelined substructure, which implements the period configuration, and multiplexers with delays to (k-1)L clock cycles on its inputs.
The hardware volume of the resulting structure, not to account registers, is estimated by the formula:
Θ’S = nA + 10nM + 0,57LnD ,
where nA and nM is the adder and multiplier number, which is equal to the number of nodes of additions and multiplications in the subgraph of SDF; nD is the number of reversed edges, or delay lines in the filter stage.
The register number in the structure depends on the topology of the subgraph, on the delay distribution between reversed edges, and can be estimated as the number which is proportional to L. As a result, if the subgraph number is equal to L, then the structure has the minimum number of registers, adders and multipliers. This is proven by the fact that by this condition exactly L nodes of delay, addition, and multiplication are mapped into respective PU nodes, and all of them are fully loaded.
5. Filter synthesis example
Consider the example of the low pass filter synthesis using the methods described in [9]. The filter consists of four sequential stages with the delays multiplied by 1, 2, 4, and 8. First three stages have the transfer function as the bireciprocal filter has. The last stage forms the sharpness of the whole filter. Each stage is implemented on the base of the allpass filter, and therefore it has stable characteristics. The transfer function of a single (first) stage is the following
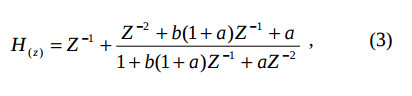
where b regulates the pass band cutoff frequency, a regulates the filter sharpness. This filter is effectively implemented using the lattice wave digital filter structure, which provides the minimum of multipliers [11].
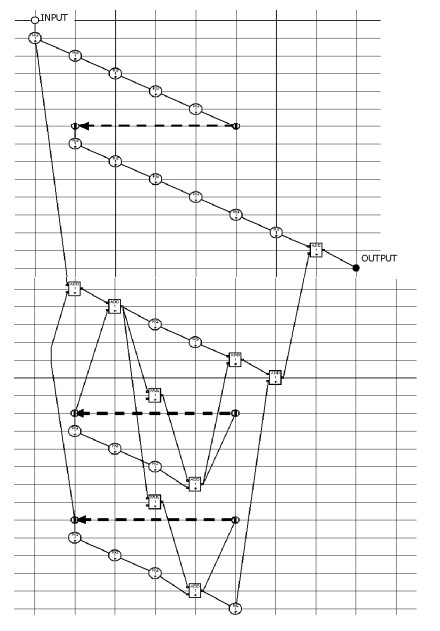
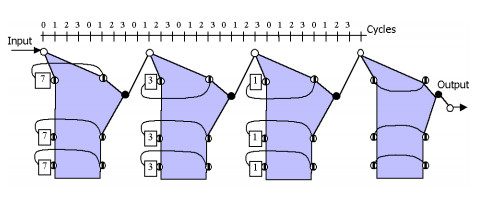
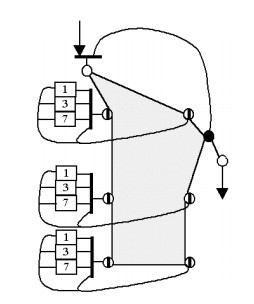
On the first step of the synthesis the balanced algorithm subconfiguration is formed which is shown on the Figure 2. On this figure the register nodes are signed by large circles, reverse edges are signed by the dotted arrow, and border nodes – by small circles. The time axis is horizontal and the space axis is vertical.
On the second step L=4 subconfigurations are connected together. The resulting configuration is shown on the Fig. 3. And on the third step the filter structure is derived, and its FSM is synthesized. The Figure 4 illustrates the derived structure configuration. In the figures the colored polygons represent the subconfiguration shown on the Figure 2.
The filter implementation consists in transformation its algorithm configuration into VHDL description and then in configuring it in FPGA.
When such a filter is designed by the usual method then its structure consists of four separate stages connected in chain. Each stage has 7 adders 2 multipliers and 3 registers for pipelining. Besides these stages have three registered delays, each of them has 1, 2, 4 and 8 registers, which can be implemented on SRL16 units. The resulting hardware volume is equal ΘSВ = 132. In the critical path of this structure 4 adder are set, i.e. the clock cycle period is equal to ΘТВ = 4ТS.
The synthesized structure has 2 multipliers, 7 adders, 26 registers and registered delays, and 7 four input multiplexers. Its hardware volume is equal to ΘS=65,5. The critical path delay is equal to the delay of a single adder or multiplier, i.e. ΘТ = ТS, and the cycle period is equal to LТS=4ТS. Comparing the derived figures, the proposed structure has twofold smaller hardware volume than the usual structure has, and has the same throughput.
6. Dynamically tuned Digital filter
In the representation the digital filter that is tuned dynamically (on the fly) is exposed. This filter design is similar to the design example shown above. The main idea is that the stage coefficients, and the chain length can be exchanged during the filter operation considering the properties of the transfer function (3). Up to 8 stages are connected into chain. As a result, the bandpass edge frequency is tuned in the range of (0,015-0,4)fS. The suppression level is not less than 75-80 db, and the filter steep slope is higher than 100 db per octave. The 12-bit length frequency code regulates the edge frequency.
The filter was implemented in Xilinx Virtex4 FPGA device. Its hardware volume occupies 706 CLB slices and three multipliers. Due to the full pipelining the maximum clock frequency is higher than 200 MHz. As a result, the filter has small hardware volume, high characteristics, and can operate with the signals with the sampling frequencies up to 25 MHz. The filter structure and its control is so complex that its design would be impossible without a proposed method use.
7. Rational fraction numbers in the IIR filters
High quality IIR filters must be implemented with the increased computation precision to preserve the dramatic truncation error increase. For this purpose the variable bit width is increased up to two fold increase, and often the floating point data is used. As a result, the hardware volume is increased and the filter throughput is decreased.
It is proposed to implement the IIR filter calculations using the rational fraction numbers which are used, for example, in the linear algebra problem solving in FPGA [12]. Then the data are represented by the n-bit numerator and n-bit denominator. The rational fraction multiplier consists of two usual multipliers, i.e. its hardware is in two times less volume than the multiplier for the 2n-bit integers has. The fraction adder has three multipliers and one adder of n-bit integers. To preserve the high precision, after each fraction operation numerator and denominator of the result are normalized to some bit number (2-8).
The disadvantage of this approach is that need of division of numerator to denominator to represent the results as the usual integer data. But if the DSP system implements a set of complex algorithms including multirate filtering, linear algebra problem solving, DFT, which use the rational fraction calculations as well, then such final data transfer has not high comparative complexity.
The ALU which calculates the rational fractions has more hardware volume than ALU for integers. But this volume more than in 2 times less than the floating point ALU has, and its throughput is higher than one of the floating point ALU or 2n-bit integer ALU has. The latent pipeline delay of such ALU is equal to 3-6 clock cycles, and is sufficiently less than the latent delay of the floating point ALU.
The direct use of the rational fraction ALU in the IIR filter with the parameter L=1 is not effective due to its high latent delay. But it is not sufficient when L>(2-5), i.e. when the proposed methods of SDF mapping are used.
Conclusion
A method of pipelined DSP application specific processors is proposed which provides adder, multiplier, and multiplexor hardware minimization due to the
utilization of properties both DSP algorithms and FPGA architectures. The synthesized processors have the minimized clock cycle, and implement the DSP algorithms in the pipelined mode with the given period of L clock cycles.
The proposed methods of design of multistaged DSP filters with multiple delays provide the minimized clock period and hardware volume by the given limitations (period L, cost function Θ’S, SDF with equal subgraphs). These methods were proved in designing the multistage wavepropagation filters. This design shows that the hardware volume can be decreased in two times comparing to the hardware volume of usual filters.
The rational fraction calculations in IIR filters are proposed, which by use of proposed methods helps to achieve the high speed precise computations on the processors with minimized hardware volume.
This work was partially funded by the Science and Education Ministry of the Republic Poland, grant N515 002 32/0176.
References
[1] S. S. Bhattacharyya, R. Leupers, P.Marwedel, “Software Synthesis and Code Generation for Signal Processing Systems” IEEE Trans. on Circuits and Systems—II: Analog and Digital Signal Processing, 2000, V47, №9, pp.849-875.
[2] The Systhesis Approach to Digital System Design / Ed. P. Michel, U.Lauther, P.Duzy, Kluwer Academic Pub., 1992.
[3] Eles P., Kuchinski K., Zebo P., System Synthesis with VHDL, Kluwer Academic Pub., 1998.
[4] System Generator for DSP. Getting Started Guide. August, 2007, -85p. see http://www.xilinx.com
[5] Ju.S.Kanevski, A.M.Sergienko, A.A. Guzinski, “Method for Mapping Unimodular Loops into Application Specific Parallel Structures”, Proc. of the 2-nd Intern. Conf. “Parallel Proc. and Appl. Math. PRAM’97” , Zakopane, Poland, 1997, pp. 362-371.
[6] A.Sergiyenko, J.Kaniewski, O.Maslennikov, R.Wyrzykowski, “Mapping regular algorithms into processor arrays using software pipelining” Proceedings of the 1-st Int. Conf. on Parallel Computing in Electrical Engineering, Bialystok, Poland, 2-5 Sept., 1998. pp.197-200.
[7] Ju.S.Kanevski, L.M.Loginova and A.M.Sergienko, “Structured Design of Recursive Digital Filters” Engineering Simulation, OPA, Amsterdam B.V., 1996, Vol. 13, pp. 381-389.
[8] A.Sergyienko, J.Kaniewski, A. Arefjev, D.Kortshev. A Method for Mapping DSP Algorithms into Pentium MMX Architecture. Proc 3-d Int. Conf. On Parallel Processing and Applied Mathematics, PPAM’99, Kazimierz Dolny, Poland, Sept. 14-17, 1999, pp.348-356
[9] H. Johansson , L. Wanhammar, “High Speed Recursive Filter Structures Composed of Identical All-Pass Subfilters for Interpolation, Decimation, and QMF Banks With Perfect Magnitude Reconstruction”, IEEE Trans. on Circuits and Systems – II Analog and Digital Signal Processing, 1999, V46, N1, Jan., pp.16-28.
[10] J. G.Chung, K.K.Parhi, “Pipelined wave digital filter design for narrow-band sharp-transition digital filters” Proc. IEEE Workshop VLSI Signal Processing, La Jolla, CA, 1994, pp. 501-510.
[11] A. Fettweis, “Wave digital filters: Theory and practice”, Proc. IEEE, 1986, V74, N2, Feb., pp.270-327.
[12] A.Sergiyenko, O.Maslennikow, P.Ratuszniak “Implementation of linear algebra algorithms in FPGA-based rational fraction arithmetic units”, Proc.Int.Conf.The experience of designing and application of CAD systems in microelectronics. CADSM-2007, 20-24 Feb.2007 Lviv-Polyana, Ukraine. Lviv Polytechn.NU: -2007. –pp.228-234.