Алгоритмічні моделі обробки потоків даних

Опубліковано в ж. Електронне Моделювання. 2009 р.
УДК 681.3
В.П.Сімоненко, докт. техн. наук,
А.М.Сергієнко, канд. техн. наук,
Національний технічний університет України “КПІ”, Київ,
03056, пр.Перемоги, 37
тел.: 4549337
E-mail: aser@comsys.kpi.ua

Розглянуто обчислювальні моделі для задавання алгоритмів обробки потоків даних з метою вибору найбільш придатної моделі відображення алгоритму в структуру конвеєрного обчислювача.

Ключові слова: граф потоків даних, відображення алгоритму, обчислювальна система.

Вступ

За загальноприйнятим визначенням, алгоритм – це обчислювальний процес, який має початок, детерміновану послідовність дій, кінець, і який для різних початкових даних дає очікувані результати [1]. Це визначення стосується трансформуючих обчислювальних систем (ОС) без обмежень на швидкодію. У протилежних до них ОС реального часу періоди виконання алгоритмів не перевищують заданих часових обмежень. Такі ОС поділяють на інтерактивні, якщо вони реагують на вхідні дані з притаманною їм швидкістю, та реактивні, які не допускають втрати цих даних через свою недостатню швидкодію [2,3]. Персональні комп’ютери, засоби мобільного зв’язку та інші засоби цифрової обробки сигналів (ЦОС) відносяться до ОС реального часу.

Для програмування періодичних алгоритмів, що виконуються в ОС реального часу, кожна нова програмістська парадигма додає нові засоби й можливості. Так, в об’єктно-орієнтованому програмуванні програміст виконує опис об’єктів, уявляючи, що об’єкти обробляються паралельно. В дійсності, ці об’єкти обробляються на ресурсах ОС послідовно та з різними періодами [4]. Таким чином, в обчислювальній техніці зараз нас оточують, в основному, періодичні алгоритми, що обробляють потоки даних і/або команд і які потенційно є нескінченними.

Галузь ЦОС побудована саме на обробці потоків даних і тому вона найбільш яскраво відображає задачі, алгоритми та пристрої обробки таких потоків. Сучасний стан ЦОС характерний тим, що алгоритми, які забезпечують бездротовий зв’язок, компресію зображень, моделювання тривимірних сцен та ін., не можуть бути реалізовані на апаратурі персонального комп’ютера в реальному часі. Для їхньої реалізації потрібно використовувати спеціальні ОС на основі сучасних замовлених НВІС, багатопроцесорних сигнальних мікропроцесорів, а також програмовані логічні інтегральні схеми (ПЛІС). На теперішньому етапі розвитку ЦОС програміст, що розробив новий алгоритм ЦОС, має змогу негайно його впровадити, але ця змога не реалізується, якщо програміст не володіє досконало паралельним програмуванням [5].

Для досягнення високої продуктивності ОС необхідне програмування багатопроцесорних паралельних систем. Відомо, що при кількості процесорів більше чотирьох, їхнє програмування при теперішньому стані технології розробки програм перетворюється в дуже трудомістку роботу. Зараз набуває поширення парадигма багатопотокової обробки (multithreading), яка підтримується як на рівні матзабезпечення, так і на апаратному рівні сучасних комп’ютерів. Але, наприклад, в [6] доведено, що багатопотокова обчислювальна модель не гарантована від блокувань, і при переході до багатоядерних мікропроцесорів вірогідність блокувань зростає. Тому повинні бути розповсюджені нові парадигми вирішення задач обробки потоків даних.

Нові завдання, які ставить сучасний етап розвитку ЦОС, не можуть бути виконані без розробки нових методів і засобів відображення алгоритмів в НВІС і ПЛІС, програмування багатопроцесорних ОС. Така розробка можлива, перш за все, за умови нового бачення природи алгоритмів обробки потоків даних. Нажаль, у вітчізняній літературі не опубліковано систематичної інформації про алгоритмічні моделі обробки потоків даних і про їхнє застосування в практиці програмування та синтезу паралельних ОС. Ця стаття є оглядом існуючих моделей задавання періодичних алгоритмів обробки потоків даних і відображає стан наукової думки в даній галузі.

Поняття алгоритму і обчислювальної моделі

За визначенням Поста і Тюрінга, алгоритм – це обчислювальний процес, який виконується деякою моделлю обчислювача, яка зконструйована в рамках точних математичних понять [7]. Таке визначення алгоритму дає змогу, по-перше, класифікувати алгоритми за типом моделі обчислювача, по-друге, порівнювати між собою різні алгоритми шляхом їхнього еквівалентного перетворення в алгоритми, що задані на стандартній моделі обчислювача, такій, як машина Тюрінга, по-третє, конструювати такі моделі обчислювачів, які найбільш придатні для ефективного задавання того чи іншого класу алгоритмів.

Визначення алгоритму, приведене у вступі, стосується, перш за все, нейманівської моделі обчислювача. Така модель характеризується тим, що вона виконує послідовно в строгому порядку команди, які змінюють стан пам’яті обчислювача, від початкового до кінцевого. На такій моделі виконуються операторні, імперативні алгоритми.

В функціональних алгоритмах обчислення виражаються як множина тотожностей від функцій. При цьому результати функцій обчислюються тільки тоді, коли для них є відповідні вхідні дані. В функціональному алгоритмі немає обмежень на порядок обчислення функцій крім порядку, який задано залежностями по даних.

Модель обчислювача, що реалізує функціональний алгоритм, прийнято представляти у вигляді графа. В такій моделі вершини графа представляють функції або оператори алгоритму, а дуги – залежності по даних і керуванню. Реалізація алгоритму на такій моделі представляє собою передачу даних у напрямку дуг і обхід вершин у відповідності до їхньої інцидентності, наявності даних на їхніх входах або за іншими правилами. На відміну від імперативних алгоритмів, тут порядок виконання операторів є нестрогим, а паралелізм алгоритму заданий явним чином. Далі розглянемо кілька відомих графових моделей функціональних алгоритмів щоб показати їхні основні властивості.

Найбільш відомою графовою моделлю обчислень є мережа Петрі. Граф цієї мережі складається з вершин-позицій і вершин-переходів, які попарно зв’язані дугами. Виконання алгоритму в цій моделі керується наявністю міток в вершинах-позиціях, які асоціюються з даними. Якщо кількість міток на входах вершини-переходу є достатньою, то вона спрацьовує і відповідна мітка з’являється на її виході. Виконання алгоритму складається в серії спрацьовувань переходів в довільному порядку, аж поки не залишиться умов для таких подій [8].

Мережі Петрі використовуються для моделювання роботи асинхронних систем, як наприклад, протоколів обміну даними [9]. Хоча існує достатня кількість робіт [10-13], присвячених застосуванню цих мереж в проектуванні обчислювальної апаратури, вони не набули великого розповсюдження в цій галузі. Основна причина цього є та, що дуже важко аналізувати мережу Петрі, визначаючи її безпечність, відсутність блокувань та інші властивості.

Граф Карпа і Міллера (граф обчислень, computation graph) був першою обчислювальною моделлю для задавання алгоритмів обробки потоків даних [14]. Вершини такого графа – актори – представляють операції, а дуги – черги даних, причому кожній дузі призначені число міток (даних) в черзі на початку обчислень, число міток, що входять в чергу при виконанні оператора на початку дуги, число міток, що виходять з дуги при виконанні актора на кінці дуги й мінімальна довжина черги. При виконанні обчислювального процесу актори спрацьовують у відповідності з деяким розкладом і читають дані з потоків, причому дані можуть залишатись в потоках після читання. Між графом Карпа і Міллера та мережею Петрі є взаємно-однозначний зв’язок – черги даних відповідають вершинам-позиціям, а актори – вершинам-переходам [15].

В обчислювальній моделі мережі процесів Кана асинхронні процеси взаємодіють між собою через послідовні буфери даних, названих потоками, які підкоряються дисципліні перший зайшов в буфер – перший вийшов, тобто FIFO [16]. В цій моделі вершина процесу може виконувати ввід даних в довільному порядку. Але після читання даного процес блокується, поки не буде в наявності нове дане, тобто процес запускається по оператору wait on data, а саме дане вилучається. В загальному випадку, якщо буфери FIFO обмеженої глибини, ця мережа може бути заблокованою, причому неможливо встановити заздалегідь, чи відбудеться таке блокування. Тому коректне виконання алгоритму може бути гарантоване лише при динамічному складанні розкладу [17].

На відміну від мережі Петрі, в мережі процесів Кана стан даних в потоках не залежить від розкладу виконання процесів, тобто потоки даних в моделі є детермінованими [14]. Ця мережа дала поштовх для народження багатьох інших моделей обробки потоків даних, які будуть розглянуті нижче. Наприклад, граф потоків даних (ГПД) характеризується тим, що дуги мають розмітку, яка вказує, яка глибина буфера FIFO, скільки міток заходить в дугу й виходить з неї за один запуск акторів на її кінцях, вершини можуть мати різні правила спрацьовування, включаючи умовні спрацьовування.

Для класифікації моделей обробки потоків даних розглянемо визначення потоку даних і його параметри.

Класифікація моделей обробки потоків даних за типом потоку даних

Всі моделі обчислювачів потоків даних мають ту загальну особливість, що їхні компоненти – вузли, оператори, актори або процеси – з’єднані між собою потоками даних. Часто потік даних називають сигналом. В загальному випадку, потік даних – це засіб передачі скінченної або в граничному випадку, нескінченної кількості впорядкованих даних між компонентами обчислювальної моделі.

Обчислювальні моделі відрізняються між собою способом виконання потоків даних. Спосіб такого виконання залежить від певних властивостей або ознак потоку, тобто від того:

• чи потік однонаправлений, чи двонаправлений;
• чи у потока одне джерело даних, чи кілька джерел;
• чи з потока зчитує дані один процес, чи кілька процесів;
• як в потоці дані відрізняються за часом виникнення, споживання;
• як в потоці дані відрізняються між собою за порядком, як наприклад, в буфері FIFO;
• чи дозволяється в потоці дублювати дані або їх перезаписувати;
• якщо потік є чергою, чи дозволяється перевірка наявності даних в потоці, чи ні;
• чи розглядає модель час як безперервну сутність, коли сигнал – це функція від часу, чи як дискретні події, коли відлік сигналу представлений парою момент часу (номер такту) – значення, чи взагалі процеси розвиваються безвідносно до часу, коли сигнал – це впорядкована множина відліків;
• якщо потік є чергою, то чи кількість переданих даних в потік за певний проміжок часу дорівнює кількості спожитих даних, чи ні, або ця кількість змінюється динамічно;
• чи джерело й приймач даного звертаються до потоку одночасно [18-20].

Синхронні й асинхронні моделі

Останні дві приведені вище властивості потоку даних характеризують його існування в часі. Розрізняють синхронні й асинхронні потоки та відповідно – синхронні й асинхронні моделі обчислень. В асинхронному потоці момент передачі даного є довільним і він допускає довільну затримку між завантаженням даного в потік і його споживанням. Це дає можливість будь-яким чином вибирати моменти завантаження й споживання даних або спрацьовування відповідних акторів при складанні розкладу виконання алгоритму.

В синхронному потоці момент передачі даного, або групи даних зв’язаний з деякою регулярно повторюваною подією, наприклад, сигналом синхросерії, тобто цей момент визначається дискретно. Якщо такий потік не має буферної пам’яті, то завантажене в нього дане повинне бути спожите негайно або з затримкою, що не перевищує періоду синхросерії. Синхронізм потоку може досягатись за допомогою логічних умов, тобто це особливий випадок асинхронного потоку. Зате аналіз синхронних потоків і складання для них розкладу значно спрощується в порівнянні з асинхронними потоками. Розрізняють моделі з синхронізацією по синхросерії та моделі з рандеву. В останніх джерело й приймач звертаються до потоку одночасно через механізм синхронізації з квотуванням.

Модель мережі процесів Кана характеризується тим, що вона абстрагована від часу й тому є потенційно асинхронною. Завдяки цьому вона може задавати алгоритми на більш високому рівні абстракції та бути трансформованою в асинхронну або синхронну модель, наприклад, при синтезі обчислювача. Крім того, ця модель має потоки у вигляді черги, тому може задавати алгоритми, в яких кількість даних в черзі змінюється динамічно. Наприклад, мережа процесів Кана дозволяє динамічно змінювати кількість переданих даних в потік. Через це глибина буфера потоку може бути необмеженою.

Таким чином, різні моделі обробки потоків даних, перш за все, можна класифікувати за ознаками їхніх потоків. Також їх можна класифікувати за будовою їхніх процесів, акторів, операторів, типом розкладу.

Класифікація моделей обробки потоків даних за типом розкладу

Коректність задавання алгоритму на моделі обчислювача може бути перевірена або аналітично (якщо це можливо), або шляхом складання розкладу виконання обчислювального процесу на даній моделі. Розклад також складається при безпосередньому виконанні заданого алгоритму в певній ОС. Якщо структура ОС відповідає графу моделі, то складання розкладу полягає в визначенні порядку виконання операторів (акторів, процесів) і в обчисленні конкретного моменту виконання кожного оператора. Якщо структура ОС довільна, то попередньо виконують етап призначення операторів на процесори цієї ОС.

Розрізняють повністю статичний, частково статичний (self timed), повністю динамічний розклади, а також розклад зі статичним призначенням [21]. В першому випадку всі етапи складання розкладу здійснюють до виконання алгоритму в ОС, тобто під час компіляції. В другому випадку призначення операторів на ресурси й знаходження порядку їхнього виконання реалізуються під час компіляції, а власне момент виконання визначається динамічно. В третьому випадку всі етапи складання розкладу виконуються динамічно. Четвертий випадок відрізняється від третього лише тим, що призначення на ресурси виконується під час компіляції й не стосується обчислювальних моделей, в яких ці ресурси вже призначені. Згідно з трьома першими випадками можна класифікувати алгоритми та обчислювальні моделі як такі, що мають повністю статичний, частково статичний і повністю динамічний розклади.

При синтезі обчислювачів на базі НВІС і ПЛІС відповідні САПР дозволяють тільки повністю статичний розклад для вхідних алгоритмів і дуже рідко – частково статичний, як наприклад, при синтезі асинхронних ОС. Це пов’язане з тим, що результуюча ОС на рівні логічних схем повинна бути повністю детермінована з точністю до вентиля і, як правило, не допускає свого динамічного перенастроювання під час виконання заданого алгоритму [22,23]. Тому далі будуть окремо відмічатись такі моделі, що підтримують статичний розклад або такі, поведінку яких можна передбачити на стадії компіляції. Останні часто називають моделями з квазістатичним розкладом.

Класифікація моделей обробки потоків даних за типом акторів

Актор або процес, або просто оператор, який позначений вершиною графа, виконує деяку функцію при своєму спрацьовуванні. Актори можна розрізняти за умовами спрацьовування, за кількістю міток (токенів), що споживаються й генеруються ними та за внутрішньою будовою.

Якщо актор споживає й виробляє деяку кількість міток, ця кількість стабільна під час виконання алгоритму та може бути визначена під час компіляції, то такий актор є регулярним. Якщо ця кількість не є константою й може змінюватись під час виконання алгоритму в залежності від даних в потоках, то це динамічний актор. Прикладом динамічного актора є вершина перемикача, яка в залежності від наявності мітки на логічному вході сприймає мітку на тому чи іншому вході даних. Моделі з динамічними акторами можуть мати або динамічний або квазістатичний розклад.

ГПД, в якому всі актори – регулярні, одержав назву графа синхронних потоків даних (ГСПД, synchronous data flow – SDF) [24] або регулярний граф потоків даних [25]. Перша назва є сталою зараз, а друга – перегукується з назвою відповідного різновиду решітчастого графу алгоритму [26,27] й тому є рідко вживаною. Слово “синхронний” тут не означає синхронність прийому або видачі даних акторами, а лише те, що модель виконує алгоритм циклічно. Причому поведінка моделі в кожному циклі однакова – кількість спожитих і згенерованих міток є константою. В цьому контексті синхронізм стосується можливості синхронізації циклів і означає, що потоки даних змінюють свій стан синхронно з виконанням цих циклів.

Якщо кількість спожитих з кожного входу міток і згенерованих кожною вершиною міток в одному циклі є сталою, наприклад, дорівнює одиниці, то такий граф називають однорідним ГСПД (homoheneous SDF). Синонімом однорідного ГСПД є редукований граф алгоритма (РГА), назва якого походить від способу його побудови з регулярного графу залежностей по даних [26].

Якщо кількість спожитих і згенерованих вершинами міток різна то ГСПД слід назвати неоднорідним ГСПД (multirate SDF) [28]. Неоднорідні ГСПД згадуються в російськомовній літературі як “многократные” [29] або “многоскоростные” [30,31] в контексті систем цифрової фільтрації, тобто як прямий переклад слова multirate. Семантично це означає, що такий ГСПД описує систему, в якій використовуються кілька взаємно кратних частот дискретизації.

Неоднорідний ГСПД – це вдала модель для компактного задавання періодичних алгоритмів. Але його складно аналізувати, наприклад, для пошуку оптимального розкладу. Крім того, його моделювання ускладнене через можливість блокувань. Тому для аналізу неоднорідного ГСПД та синтезу на його основі ОС граф часто перетворюють в еквівалентний однорідний ГСПД [32]. Незважаючи на це, ця модель набула поширення й застосовується в широко вживаному пакеті Matlab-Simulink [33].

ГСПД завжди асоціювались з алгоритмами цифрової обробки сигналів. Однорідний ГСПД взаємно однозначно відповідає сигнальному графу або обчислювальній схемі, що має період обчислень один такт, які використовуються в цифровій обробці сигналів [30,34,35].

Розроблений такий різновид ГСПД, в якому замість одиночних міток розглядаються групи по N міток, що відповідають масивам відліків. Такий ГСПД набув назву масштабованого ГСПД (scalable SDF) [36]. Для того, щоб задати алгоритм обробки багатовимірного сигналу масштабований ГСПД був узагальнений до багатовимірного ГСПД, в якому мітки розглядаються як багатовимірні масиви з кратними розмірами, а розмітка дуг виконана за допомогою векторів, розмірність яких співпадає з кількістю вимірів масивів [37].

Існують моделі, що мають ієрархію циклів виконання в часі, причому у внутрішніх циклах кількість спожитих і згенерованих міток може бути змінною, зате сумарна така кількість є стабільною при її підрахунках у зовнішньому циклі. Такі моделі одержали назву цикло-статичних ГСПД (cyclo-static dataflow) і в них усунуто багато недоліків представлення алгоритмів неоднорідними ГСПД [38].

Граф, в якому є динамічні актори, називається динамічним графом потоків даних (ДГПД). Через обмеження по запуску акторів статичний ГСПД має вужчі можливості, ніж мережа Петрі. Зате ДГПД за своїми властивостями еквівалентний машині Тюрінга, яка, в свою чергу, більш універсальна модель, ніж мережа Петрі. Через таку універсальність ДГПД досить складно аналізувати, так як невизначена його поведінка в залежності від потоків даних. Тому деякі задачі аналізу ДГПД є невирішеними [39]. Така модель обробки потоків даних застосовується для визначення й реалізації мови VHDL, яка використовується як для моделювання, так і для синтезу ОС [33, 40].

Якщо ДГПД складається з акторів, що споживають керуючі мітки двійкового типу та регулярних акторів, то такий ДГПД називається булевським ГПД (Boolean dataflow) [38]. Більш широку область алгоритмів представляє цілочисельний ГПД, актори якого керуються цілими числами (integer controlled dataflow) [41]. Актори цих графів можна описати мовами з застосуванням операторів if-then-else або case, відповідно. На відміну від ДГПД загального виду, поведінка булевського або цілочисельного ГПД не залежить від способу складання розкладу для нього, так як вони є різновидами мережі Кана.

ДГПД може мати невелику кількість динамічних вершин, поведінку яких можна спрогнозувати, наприклад, шляхом визначення вірогідності їхнього спрацьовування й тому для них є можливість розрахувати статичний розклад для всіх вершин, крім динамічних. Такі ДГПД і їхній розклад набули назву квазістатичних [42,43].

Якщо є змога, щоб підграф квазістатичного ДГПД з динамічними вершинами склеїти в вершину, яка поводиться як статична, то такою процедурою можна перетворити ДГПД в ГСПД. В цьому випадку такий ДГПД називають ДГПД з ефективною поведінкою (well-behaved) [44].

В параметричному ГСПД актори можуть мати деякі набори функцій, а дуги – відповідні набори розміток, причому дозволяється динамічно змінювати функції та розмітки незалежно від потоків даних на період не менше одного циклу. Для такого ГСПД можливо скласти квазістатичний розклад і за своїми властивостями він схожий на цикло-статичний ГСПД [45]. В моделюючій системі PtolemyII параметричний ГСПД, як і циклостатичний, цілочисельний ГСПД впроваджені в повному обсязі. Ця система показала себе ефективною при розробці матзабезпечення для ОС обробки мультимедійних даних [33].

i>Блочний ГСПД (Blocked DataFlow, BLDF) є підмножиною параметричного ГСПД і є розширенням масштабованого ГСПД. В ньому під міткою мається на увазі пакет даних з деякою структурою і властивостями. Причому актори й дуги ГСПД виконують свої функції у відповідності з тегом, призначеним до мітки, тобто такий ГСПД є динамічним і, відповідно, такий ГСПД має квазістатичний розклад. Блочний ГСПД є вдалою моделлю для завдання алгоритмів на високому рівні для обробки, наприклад, мультимедійних даних [46].

Ієрархічні ГПД

Модель потоків даних класифікують також за ознакою: чи є модель ієрархічна чи ні. В ієрархічній моделі вершина актора сама може бути представлена деякою моделлю того чи іншого типу. При використанні мови програмування побудова ієрархії еквівалентна викликам відповідних процедур, що виконують обчислення моделей нижчого рівня. Якщо модель нижчого рівня – не вироджена, то вона може бути представлена деяким автоматом з пам’яттю. Тому часто обчислювальні моделі класифікують як такі, що мають актори з пам’яттю або без неї.

Можна одержати параметричний цикло-статичний ГСПД шляхом зклеювання множин вершин однорідного ГСПД. Таким чином, нова вершина актора включає в себе кілька вершин початкового графу й тому є ієрархічною. З іншого боку, нова вершина має комплексну функцію, що покриває функцїї зклеєних вершин початкового графу.За один цикл вона послідовно виконує обчислення цих вершин, тобто вона вже може не розглядатись як їєрархічна. Процедура такого перетворення ГСПД набула назви зкручування (folding), а одержаний граф – зкрученого ГСПД (folded SDF). Така операція є запозиченням з оптимізації програм і є еквівалентом способу зкручування циклів (loop folding). За своєю суттю зкручений ГСПД є ізоморфним графу структури деякого конвеєрного обчислювача, а зкручування ГСПД є методом синтезу таких обчислювачів [47].

Для аналізу ієрархічної моделі вона повинна припускати перетворення в однорівневу модель без ієрархії. Існують моделі потоків даних, в яких ієрархія будується динамічно, наприклад, коли процес викликає інші довільні процеси як підпрограми. Хоча така модель дає великі креативні можливості для програмістів, вона не дає змоги будувати однорівневу модель і дуже ускладнює аналіз таких моделей.

Графи залежностей по даних

Графи залежностей по даних і/або керуванню були винайдені як натуральні моделі обчислень, що задовольняють потреби компіляції й розпаралеювання програм, написаних на імперативних мовах [6,48]. В графі залежностей по даних (ГЗД) вершини-оператори зв’язані дугами, що відповідають безпосереднім залежностям між операторами в алгоритмі або програмі. Якщо в алгоритмі використовується принцип однократного присвоювання, то дугам відповідають операнди алгоритму [49]. Під час компіляції програм алгоритм розкладається на граф керування (flow graph) та направлені ациклічні графи безпосередніх залежностей (directed acyclic graph – DAG), які є ГЗД [50]. Виконання алгоритму, заданого на ГЗД, представляє собою послідовний обхід вершин у відповідності з їхнім топологічним сортуванням [51]. При використанні ярусно-паралельної форми ГЗД дозволяється одночасне виконання операторів, що відповідають одному ярусу графа. Це використовується як найпростіший і найзрозуміліший спосіб розпаралелювання алгоритмів [48].

ГЗД безпосередньо не пристосований для задавання алгоритмів обробки потоків даних. Таку обробку можна виконати тільки при послідовному виконанні алгоритму – як тільки завершаться обчислення для n-ї групи вхідних даних, починається обчислення n+1-ї групи.

ГЗД, в якому задані затримки виконання операторів, або кількість ступенів конвеєрного обчислювача, що відповідає вершині оператора, одержав назву базової ОС. Якщо в дуги ГЗД добавити вершини затримки, то можна одержати урівноважену базову ОС, в якій затримка між будь-якими двома вершинами однакова безвідносно маршруту поширення операндів між ними. Особливість урівноваженої базової ОС полягає в тому, що вона відповідає ациклічному алгоритму обробки потоку даних, тобто вона є однорідним ациклічним ГСПД, в якому розмітка дуги дорівнює кількості ступенів конвеєра відповідної вершини базової ОС [27,35].

Під час складання розкладу виконання алгоритму на ГПД будується розгортка обчислень, яка є ГЗД. Відповідно, якщо ГЗД є періодичним, то він може бути відображений в деякий ГСПД, який можна побудувати по періоду ГЗД. В такий спосіб будують РГА, що є синонімом однорідного ГСПД [26].

ГЗД регулярного алгоритму, наприклад, гніздо циклів, представляє собою періодичний або решітчастий граф, період якого є DAG тіла цикла [27,52]. Існує методологія відображення такого ГЗД в граф систолічного процесора [27,53,54]. Вона є однією з небагатьох методологій, яка дала змогу формальним чином перетворювати обчислювальний алгоритм в паралельну структуру спеціалізованого обчислювача. Важливо відмітити, що граф систолічного процесора по суті є однорідним ГСПД і таким чином, ГСПД можна будувати використовуючи ефективні і формальні методи синтезу систолічних процесорів [26].

Взаємні відношення графових моделей обробки потоків даних виражені графом на рис.1.

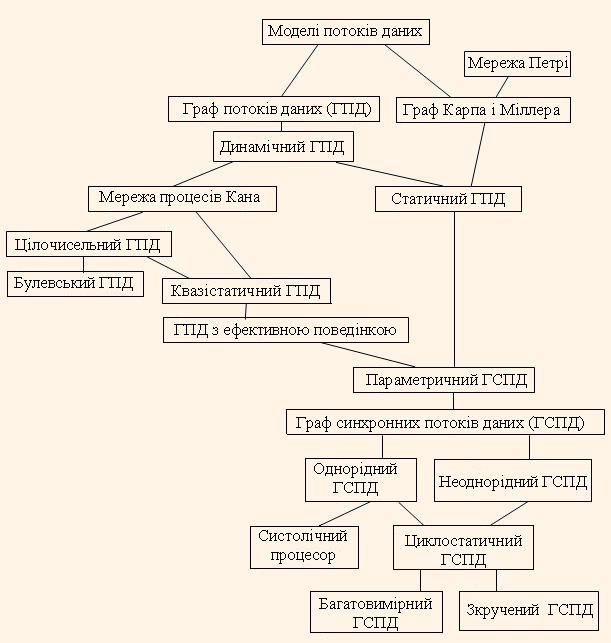
Аналізуючи цей граф і вище приведену класифікацію моделей можна зробити наступний ряд висновків.

Висновки щодо вибору представлення алгоритму обробки потоків даних

ГПД призначений для задавання різних алгоритмів обробки потоків даних і має багато різновидів, створених для спрощення його аналізу, адаптації до окремих класів алгоритмів, збільшення виразності представлення цих алгоритмів. Алгоритм, заданий на ГПД, показує як одержується результуючий потік даних і не задає точний порядок обчислень. Конкретне відображення такого алгоритму в ОС полягає в знаходженні оптимального розкладу і відображенні вершин графа в процесорні елементи ОС, що є NP-повною задачею. Вибір того чи іншого різновиду ГПД залежить від предметної області застосування алгоритму (моделювання або обробки даних/сигналів, характер сигналів) і способу його виконання (апаратного чи програмного).

З метою використання для системного синтезу апаратних пристроїв для обробки потоків даних найбільш придатна модель ГСПД, а також її удосконалення – параметричний, цикло-статичний і багатовимірний ГСПД. Також можуть бути використані моделі квазістатичного ДГПД і ДГПД з ефективною поведінкою, для яких також можна складати розклад з властивостями статичного розкладу. Ієрархічні моделі, що складаються з вищеназваних графів, можуть також бути використані, так як вони допускають розгортки до однорівневої моделі.

Слід приділяти більше уваги однорідному ГСПД через простий його аналіз, і через те, що можливі еквівалентні перетворення в нього інших типів ГСПД. Набувший популярності підхід відображення регулярних ГЗД, в тому числі ГЗД систолічних алгоритмів, необхідно приводити до відображення ГСПД, який є ефективною формою представлення таких ГЗД. ДГПД, як і мережі Петрі, можуть бути ефективно впроваджені тільки в ОС з програмною реалізацією алгоритмів, так як вони потребують динамічного складання розкладу, яке до того ж може бути неуспішним через можливі блокування.

Застосування ГСПД для синтезу конвеєрних ОС.

Конвеєрна ОС представляє собою багатоступеневий апаратний обчислювач, який обробляє потоки даних. Його структура може бути одержана шляхом відображення ГСПД. Вище було згадано, як конвеєрна ОС одержується одиничним відображенням зкрученого ГСПД. В [55] запропоновано представляти однорідний ГСПД в багатовимірному просторі. Це дало змогу цілеспрямовано шукати як структуру ОС, так і розклад виконання алгоритму на ній. В [56, 57] цей підхід удосконалено з метою мінімізації апаратних витрат ПЛІС, в якій реалізується конвеєрна ОС. ДГПД з ефективною поведінкою відображається в конвеєрну ОС за методом, запропонованим в [57]. Цей метод дає змогу формально відображати алгоритми з операторами керування в структуру конвеєрних ОС з заданим періодом обчислень, що мають мінімізовані апаратні витрати і високу тактову частоту. При цьому через те, що результатом є опис ОС на мові VHDL, метод дає змогу не будувати власне структуру ОС і розклад виконання алгоритму, а перекласти це завдання на компілятор-синтезатор проекту для ПЛІС.

Висновки

Граф потоків даних (ГПД) представляє собою натуральну модель для задавання алгоритмів обробки таких потоків. Динамічні ГПД мають найширші можливості для задавання алгоритмів, але їхній аналіз ускладнений і вони можуть мати блокування. Через це вони застосовуються, в основному, тільки в системах з динамічним розкладом і не придатні для синтезу конвеєрних обчислювальних систем.

Конвеєрні ОС слід проектувати шляхом відображення графів синхронних потоків даних (ГСПД) або ГПД з ефективною поведінкою і квазістатичних ГПД, які мають ряд властивостей таких самих, як у ГСПД. Менша виразність і більша трудомістськість представлення алгоритму на моделі однорідного ГСПД компенсується тим, що при представленні такого ГСПД в багатовимірному просторі його відображення в конвеєрну структуру виконується формально з одержанням мінімізованих апаратних витрат.

1. Минский М. Вычисления и автоматы.-М.: Мир. –1971. – 264с.
2. Berry G. Real Time programming: Special purpose or general purpose languages /Information Processing, G. Ritter, Ed. Elsevier Science Publishers B.V. (North Holland) -1989. -v.89. -p. 11-17.
3. Lee E.A. Embedded Software /Advances in Computers, M. Zelkowitz, ed. -Academic Press, London, –2002. -V.56. –29p.
4. Грэхем И. Объектно-ориентированные методы. Принципы и практика. — 3-е изд. — М.: «Вильямс», 2004. — 880 c.
5. Сергиенко А.М. 5,5 десятилетий цифровой обработки сигналов // Argс&Argv. –2006. -№1. –с.19-25.
6. Lee E. A. The Problem with Threads // IEEE Computer. –2006.–V.39.- №5. –Р.33-42.
7. Котов В.Е. Введение в теорию схем программ. –Новосибирск: Наука.-1978. –258 с.
8. Петерсон Дж. Теория сетей Петри и моделирование систем.-М:Мир.-1984.-264с.
9. Системы параллельной обработки/ под ред. Д.Ивенса. – М.:Мир. – 1985. – 413 с.
10. Maciel P., Barros E., Rosenstiel W. A Petri Net Model for Hardware/Software Codesign // Design Automation for Embedded Systems. — 1999. №4. — P. 243–310.
11. Eles p., Kuchinski K. Peng Z. System Synthesis with VHDL. Kluwer Academic Pub. –1998. –370 p.
12. Корректность параллельных вычислительных процессов / С. М. Ачасова, О. Л. Бандман ; Отв. ред. Н. Н. Миренков; АН СССР, –Новосибирск: Наука, Сиб. отд-ние, ВЦ. –1990. –252 с.
13. LIN B. Efficient compilation of process-based concurrent programs without run-time scheduling. // Proceedings of Design, Automation, and Test in Europe (DATE) (Paris), 1998. –p.211–217.
14. Карп Р. М., Миллер Р. Е. Параллельные схемы программ – перев. Кагр R. M., Miller R. E., Parallel Program Schemata // Journal of Computer and System Sciences, 3 -1969 –р.147—195 / в кн..Кибернетический сборник. Вып13./ ред.Лупанов О.Б. –с.5- 30.
15. Системы параллельной обработки /под ред. Д.Ивенса, – М.:Мир. – 1985. – 413с.
16. Gilles Kahn G. The semantics of a simple language for parallel programming // In Proc. IFIP Congress‘74. ‘North-Holland Pub. Comp. ‘1974. ‘ p 471–475.
17. Buck J.T. Scheduling Dynamic Dataflow Graphs with Bounded Memory using the Token Flow Model. PhD thesis. – University of California, Berkeley. –1993. – 177р.
18. Caspi E. Design Automation for Streaming Systems. PhD thesis. – University of California, Berkeley. –2005. – 281р.
19 Lee E., Sangiovanni-Vincentelli A. A framework for comparing models of computation. //IEEE Trans. on Computed-Aided Design for Integrated Circuits and Systems. –V17. –1998. –№12. р.1217–1229.
20. Edwards S., Lavagno L.,Lee E.A., Sangiovanni-Vincenelli A. Design Embedded Systems: Formal Models, Validation, and Synthesis //Proc. IEEE. –V85. – N3. – 1997. – p.366-390.
21. Lee E. A. and Ha S. Scheduling Strategies for Multiprocessor Real-Time DSP // Proc. of IEEE GLOBECOM, Nov. –1989. – p.1279-1284.
22. Camposano, R., Saunders, L.F., Tabet, R.M. VHDL as Input for High-Level Synthesis // IEEE Design & Test of Computers. –1991.–March. –p.43-49.
23. IEEE Standard For Verilog Register Transfer Level Synthesis (IEEE Std 1364.1 –2002). – IEEE. –NY. – 2002. –100p.
24. Ли Е.А., Мессершмитт Д.Г. Вычисления с синхронными потоками данных// ТИИЭР -1987.-Т. 75.-№ 9.–с. 107-119. перевод Е. A. Lee and D. G. Messerschmitt, “Synchronous Data Flow,”// IEEE Proceedings, –Sept. –1987.
25. Buck J.T. Scheduling Dynamic Dataflow Graphs with Bounded Memory using the Token Flow Model. PhD thesis. – University of California, Berkeley. –1993. – 177р.
26. Рао С.K., Kайлат T. Регулярные итеративные алгоритмы и их реализация в процессорных матрицах // ТИИЭР. –1988.-76, -№ 3, – C. 58-69.
27. Воєводин В.В. Математические модели и методы в параллельных процесах. – М: Наука. –1986. – 296с.
28. Edward A. Lee Е.А. Recurrences, Iteration, and Conditionals in Statically Scheduled Block Diagram Languages / VLSI Signal Processing III, R.W. Brodersen and H. S. Moscovitz, ed-s. IEEE Press, New York, 1988.-р.330-340.
29. Гольденберг Л.М. и др.Цифровая обработка сигналов: Справочник. –М.:Радио и связь. –1985. –312с.
30. Сергиенко А. Б. Цифровая обработка сигналов (2-е изд.). СПб: Питер.- 2006. – 751 с.
31. Вайдьнатхан П.П. Цифровые фильтры, блоки фильтров и полифазные цепи с многочастотной дискретизацией. Методический обзор // ТИИЭР, -1990.-т. 78. № 3. -С. 77-120.
32. Lee E.A., and Messerschmitt D.G. Static scheduling of synchronous datafow programs for digital signal processing. //IEEE Transactions on Computers, vol. C–36, -1987. -№1, -p. 24–35.
33. Lee, E.A. and Neuendorffer S. Concurrent models of computation for embedded software //IEE Proc.-Comput. Digit. Tech., Vol. 152, No. 2, March 2005. –p. 239 – 250.
34. Оппенгейм А.В. Шафер Р.В. Цифровая обработка сигналов. – М.:Связь. –1979. 416с.
35. Сергиенко А.М. VHDL для проектирования вычислительных устройств. – Киев: Диасофт. –2003. –200с.
36. Ritz S., Pankert M., and Meyr H. Optimum vectorization of scalable synchronous dataflow graphs.//Proc. Int. Conf. on Application Specific Array Processors. –October. -1993. –p. 285-296.
37. Lee. E. A. Representing and exploiting data parallelism using multidimensional dataflow diagrams. //Proc.Int. Conf. on Acoustics, Speech, and Signal Processing. –April 1993. –p.453–456.
38. Bilsen G., Engels M., Lauwereins R., Peperstraete J. Cyclo-static dataflow //IEEE Trans. on Signal Processing. –V44. –1996. №2. – р.397–408.
39. Buck J.T. Scheduling Dynamic Dataflow Graphs with Bounded Memory using the Token Flow Model. PhD thesis. – University of California, Berkeley. –1993. – 177р.
40. Сергиенко А.М. Особенности VHDL как языка параллельного программирования.//Электрон. Моделирование. –Т 25.–2003.-№ 3.-с.115-123.
41. Buck. J.T. Static scheduling and code generation from dynamic dataflow graphs with integer-valued control streams. // Proc.28-th Asilomar Conf. on Signals, Systems, and Computers, -1994, Nov. -V1. – p. 508-513.
42. Edward A. Lee Е.А. Recurrences, Iteration, and Conditionals in Statically Scheduled Block Diagram Languages in VLSI Signal Processing III, ed. R.W. Brodersen and H. S. Moscovitz, IEEE Press, New York, 1988.-р.330-340.
43 Edward A. Lee. Е.А. Consistency in Dataflow Graphs. IEEE Trans. on Parallel and Distributed Systems, vol. 2, no. 2, April 1991 –р.223-235.
44. Gao G. R., Govindarajan R., Panangaden P. Well-Behaved Dataflow Programs for DSP Computation // Proc. ICASSP 1992 San Francisco, CA, March. – V5. –1992. –p.561–564.
45. Bhattacharya B. and Bhattacharyya S.S. Parameterized Dataflow Modeling for DSP Systems// IEEE Trans. on Signal Prcessing. -V 49. –N10. –2001. – p.2408-2421.
46. Ko D. and Bhattacharyya S. S. Modeling of block-based DSP systems. // Proceedings of the IEEE Workshop on Signal Processing Systems, Seoul, Korea, -August, -2003. –p. 381-386.
47. Parhi K.K., Wang C.Y. and Brown A.P. Synthesis of control circuits in folded pipelined DSP architectures. IEEE J. Solid-St. Circ. 27 (1992), p. 29–43.
48. Поспелов Д.А. Введение в теорию вычислительных систем. –М.:Сов.радио. –1972. – 280с.
49. Сир Ж.-К. Метод потока операндов в моногопроцессорных системах типа МІМD/ – в кн. Системы параллельной обработки /под ред. Д.Ивенса, – М.:Мир. – 1985. – 413с.
50. Ахо А., Сети Р., Ульман Дж. Компиляторы: Принципы, технологии, инструметы. –М.С-П.К. –2003. –768с.
51. Евстигнеев В.А. Применение теории графов в программировании. – М.:Наука. –1985. –350 с.
52. Воеводин В.В., Воеводин Вл.В. Параллельные вычисления. -СПб.: БХВ-Петербург, -2002.-608 с.
53.Кун С. Матричные процессоры на СБИС. –М.: Мир. –1991.–672с.
54. Каневский Ю.С. Систолические процессоры. Киев:Техніка. –1991. –172 с.
55. Каневский Ю.С., Овраменко С.Г., Сергиенко А.М. Отображение регулярных алгоритмов в структуры специализированных процессоров // Электрон. моделирование.-2002.-Т.24.-№2.-С. 46-59.
56. Симоненко В.П., Сергиенко А.М.Отображение периодических алгоритмов в программируемые логические интегральные схемы //Электрон. моделирование. – 2007. – Т.29. -№2. –С.49-61.
57. Сергієнко А.М. Синтез структур для виконання періодичних алгоритмів з операторами керування // Вістн. Націон. Техн. Університету України „КПІ”. Сер. Інформатика, управління та обчислювальна техніка. -2008. –№47. –С.62-68.