Tensor approach to the application specific processor design
Proc.10 th Int. Conf. “The Experience of Designing and Application of CAD Systems in Microelectronics”, CADSM’ 2009, 24-28 Feb. 2009. –IEEE Library. –2009. –Р. 146-149.
Tensor Approach to the Application Specific Processor Design
Oleg Maslennikow, Oleg Maslennikow − Polytechnica Koszalinska, Poland, E-mail: oleg@moskit.ie.tu.koszalin.pl
Anatolij Sergiyenko, Yurij Vinogradow − National Technical University of Ukraine E-mail: aser@comsys.ntu-kpi.kiev.ua Anatolij Sergiyenko, Yurij Vinogradow
Abstract – A method for mapping an algorithm, which is represented by the loop nest into the application specific structure is proposed. The method consists in translating the loop nest into the tensor equation. The tensor equation represents a set of structural solutions. The optimized solution finding consists in solving this equation in integers. The proposed limitations to the parts of the tensors help to derive the pipelined structure and simplify the mapping process. The method is illustrated by the example of the IIR-filter structure synthesis. It is intended for mapping DSP algorithms into FPGA.
Keywords – Algorithm mapping, SDF, DSP, FPGA.
I. INTRODUCTION
At present, the field programmable gate arrays (FPGAs) are widely used to implement the high-speed DSP algorithms. But its programming is usually consists in the functional network drawing, which contains the ready to use modules. The design of such modules, or the programming tools like module generators remains the very complex task. This task is formalized now for the acyclic algorithms like FIR filters, and is still under investigations for the cyclic algorithms like IIR filters [1,2]. Therefore, the development of the programming tools which help to map the DSP algorithms into the networks, which are adapted to the FPGA architecture are of demand.
Consider a DSP algorithm, which can be represented by a set of recurrent equations or a loop nest. In the kernel of the regular loop nest stay one or a set of assignments like:
Sti: a[I] = f(a[I+D1 ], b[I+D2 ],…),
where I is an index vector, which represents a point in the iteration space, Dj is an index increment vector of the j-th variable, which represents the data dependence between I-th, and (I+Dj )-th iterations. The irregular loop nest can be remapped into the regular one by the data pipelining or global transfer removing techniques [3,4].
If the loop kernel has a set of independent operators Sti, then this set can be represented as a single vector I in the iteration space. The methods of the systolic array synthesis are well known which utilize the mapping of such algorithms [3-5]. These methods are based on the affined transformation with the matrix P of the iteration space Zn , I ∈ Zn into the subspace of structures Zm and events Zn-m , so as the operator Sti belonging to the iteration I is calculated in the processor unit (PU) with the coordinates Ks = Ps I in the clock cycle marked by Kt = Pt I, Ks ∈ Zn , Kt ∈ Zn . If we consider the usual situation when n − m = 1, then the conditions of such a mapping are Dj Pt ≥ 0 (monotony condition) and detP ≠ 0 (injection condition).
The systolic array synthesis methods have a set of limitations, which do not provide their direct utilization in the DSP system design. They consider that operators St i , from a single iteration must be implemented simultaneously and their duration must be equal no more than a single clock cycle. Therefore, the complex operators could not be implemented in the pipelined mode.
In the representation a new method of DSP application specific processor design is proposed on the base of mapping the algorithms, which are given by the regular loop nests. The resulting processors have the pipelined ALUs and fit effectively the modern FPGAs.
II.INITIAL DATA FOR THE SYNTHESIS
Consider the a single loop algorithm:
for i = 1, Ui do (y1 (i), ..., yp (i)) = f(x1 (i − di1 ), ..., yq (i − diq )) end.
(1)
Here the function f is calculated using Uj binary assignments Stj . Therefore, the algorithm (1) can be
represented as the following:
for i = 1, Ui do
{statement St1 }
. . .
Stj : y[i,j] = φj,k (y[i-di1, j], y[i-di2, j])
. . .
{statement Stuj}
end,
(2)
where φj,k(x,y) is the operator of the k-th type, which is implemented at the operands x, y. This loop can be transformed into the next three level loop nest, such that in the (i, j, k)-th iteration only j-th operator of k-th type is implemented.
for i = 1,Ui do
for j = 1,Uj do
for k = 1,Uk do
if (j,k) ∈ Φ then y[i,j] = φj,i (y[i − di1, j], y[i − di2, j])
end
end
end,
(3)
where Φ is a set of allowed couples (j,k), which give type and implementation order of operators in the algorithm (3).
As a result, the loop (1), which contains a set of different operators, can be transformed into the loop nest of three cycles (3), and its calculations are mapped into the three dimensional iteration space K3 = {1 ≤ i ≤ Ui, 1 ≤ j ≤ Uj, 1 ≤ k ≤ Uk } ⊂ Z3. The loop nest of higher dimensions can be derived analogously. Each operator is represented in the space K3 the vector Ki ∈ K3. The data dependence between operators, represented by Ki , Kl , is equivalent to the dependence vector Dj = Ki − Kl.
In the resulting structure each processing unit (PU) is specialized to implement a single function φk. The base set of such PUs for DSP applications contains the simplest PSs like adder, multiplier, ROM. Their local memory is the FIFO buffer, or a single result register.
III. MAPPING THE REGULAR LOOP NEST INTO THE PROCESSOR STRUCTURE
In the methods [3-5] the algorithm graph GA is represented in the n-dimensional space Zn . Hence GA is the regular lattice graph. It is represented by its compact form of a set of different vectors-edges Dj of data dependences. If the loop nest contains a set of operators like (2), then the compact form is the synchronous dataflow graph (SDF) or the scalable SDF [6]. This oriented graph has N operators-nodes Ki, which are connected by respective dependence vectors-edges Dj. Consider the following algorithm:
for i = 1, N do
for j = 1, M do
St1 : a[i,j] = b[i − 1, j − 1];
St2 : b[i,j] = a[i, j];
end
end.
This algorithm is represented by the SDF graph shown in the Fig.1.
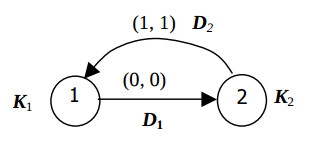
Vectors D1 and D2 represent the data a, b movings between operators St1 and St2. They labeled by the vectors of relative transfer delays (0, 0), and (1, 1). To represent the SDF graph GAR in the n-dimensional space both the matrix D of the vectors Dj of data dependences and the matrix K of the vectors Ki are needed. Here the vector K i is equal to the coordinates of
the i-th operator node. An incident matrix A of the graph GAR is needed to impress the linear dependence between both matrices K and D:
D = KA; (5)
A set of matrices K, D and A form, so called, algorithm configuration KA. Due to its nature, the matrices A, K, D are tensors of both algorithm and resulting structure, and the equation (5) is the tensor equation. In [7] it is shown that the properties of many technical objects can be described by the tensor equation. Due to the tensor theory, the complex technical system can be described by its tensor. The tensor is the generalized matrix, which can be exchanged by the allowed transformations. Therefore, a set of different implementations of a system can be described by a tensor, and one implementation can be transferred to another one by some transformation of its tensor. The system synthesis consists in building of the tensor equation, and in directed search of such tensor transformation, which minimizes the effectiveness criteria. In this representation it is shown how to find the optimized structural solutions by the algorithm mapping using the principles of the tensor theory.
The next definitions and relations are true for the configuration KA. Configuration KA is correct, if Ki ≠ Kj ; i,j = 1,…,N, i ≠ j, i.e. if all the vectors-nodes are placed separately in the space Zn.
A back linear dependence between configuration matrices is present, i.e.
K = D0A0-1, (6)
where A0 is the incidence matrix of the maximum spanning tree of the graph GAR, D0 is the matrix of the vectors-edges of this tree, including the base vector which connects the graph node with the coordinate system.
The sum of vectors-edges Dj, belongig to a graph cycle, must be equal to a zero, i.e. for the i-th cycle
Σjbi,jDj = 0, (7)
where bij is the element of the i-th row of the cyclomatic matrix of the graph GAR.
Configurations CA1 = (K1, D1, A1) and CA2 = (K2, D2, A2) are equivalent if they are correct and represent an algorithm graph, i.e. A1 = A2. Correct configuration CA1 is equivalent to the configuration CA2 iff A1 = A2 and K2 = F(K1), where F is the injection function. For example, the following transformations give the equivalent configurations: vector Ki transposition in the space Zn, row or column transposition of the matrix K1, multiplication of the matrix K1 to the non-singular matrix P.
Due to the tensor theory, any tensor object description must have the invariant tensor, which is immune to any tensor transformations. Here the matrix A and its submatrix A0 represent the invariant tensors. The matrix K codes some variant of the synthesized structure. The structure optimization consists in generating of equivalent configurations, which are different in their matrices K, and in selection of the best one due to the some criterion.
The processor structure graph Gs is represented by its structure configuration CAs = (Ks, Ds, A), where Ks is the matrix of vectors-nodes KSi ∈ Zm, which give the PU coordinates, and DS is the matrix of vectors-edges Dsj ∈ Zm, which represent the connections between PUs, m < n.
The event configuration CT = (KT,DT,A) consists of the matrix KT of the vectors KTi∈ Zn-m, matrix DT of vectors DTj, and matrix A. Here vectors KT represent the events of the operator implementation. In the correct configuration CT vector DTj = KTl − KTi means that the operator, represented by KTi, must precede the operator, represented by KTl.
The timing function R(KTi) = ti performs the mapping of the space of events Zn-m to the time axis, and derives the time of the operator implementation.
The configuration CT is correct, in other words, the precedence condition is true if for any couple of vectors KTi and KTl the inequality is true R(KTl) > R(KTi), where KTi precedes KTl.
If the function R is linear and monotonous one then the configuration CT is correct iff DTj ≥ 0, j = 1,…,M, where DTj the vectors-nodes of the SDF, which are not marked by the relative transfer delays (or zeroed ones).
The function R(DTj) gives the delay between the variable computing in one PU and entering the another PU, i.e. the higher limit of the FIFO buffer length.
Consider the mapping of the algorithm (2) into the structure, which calculates the loop kernel in the pipelined mode with the period of L clock cycles. When this algorithm is represented in the three dimensional index space, the vectors K = (j, k, i)T, where j,k,i means operator number, operator type, and cycle number respectively. Similarly the additional dimension q of the clock cycle is added to the algorithm configuration, then K = (j, k, i)T. The vector-edge, which represents the interiteration dependence, is equal to Db =(0,0,−p,0), where p is the distance between iterations.
Algorithm configuration CA is equal to the composition of structure configuration CS and event configuration CT, and if Kl = (j, k, i, q)T, then KSl = (j, k)T and KTl = (i, q)T. In the vector KSl = (j,k)T , the coordinates j,k are equal to the PU number, where the l-th operator of the k-th type is implemented.
Firstly the space component of the mapping is searched. The matrix KS forming is the combinatorial task. By this process MK operators of k-th type are distributed among more than ]MK/L[ PUs of the k-th type. In the matrix KS MS groups of equal columns are formed, each of them contains up to L columns, where MS is the PU number in the resulting structure. The j-th PU has the maximum loading if the number of columns with the j-th coordinate is equal to L. Then the matrix DS is derived from the equation DS = KSA.
The time component of the mapping represented by the matrices KT and DT is searched with respect to the conditions of the correctness of the algorithm configuration and event configuration, and equation (7). Besides, the algorithm is implemented correctly with the iteration period L iff
∀KTi ∈ KT (KTi = (i, q)T, i ≥ 0, q ∈ (0, 1,…,L-1)).
The strategies of searching of the space and timing components can be investigated in the following example of the structure synthesis.
IV. EXAMPLE OF THE PROCESSOR SYNTHESIS
Consider the synthesis of the second order IIR filter structure, which calculates the equation:
y[i] = x[i] + a ⋅ y[i−2] + b ⋅ y[i−1].
This equation is calculated by the following loop:
for i = 1, N do St1: y1 [i] = a*y[i−2]; St2: y2 [i] = b*y[i−1]; St3: y3 [i] = x[i] + y1 [i]; St4: y[i] = y2 [i] + y3 [i]; end.
The SDF graph of this algorithm is shorn in Fig.2.
Each operator is calculated no less then a single clock cycle. The loaded edges mean the delays of the variable y[i] to one and two cycles, and could not express the delay of the operator St4 . Therefore, in these edges additional nodes are set. The modified SDF graph is shown in the Fig.3.
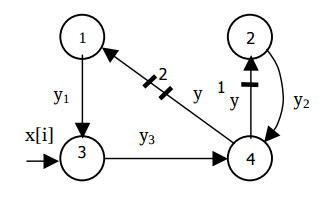
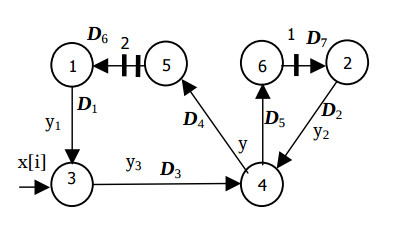
This graph represents the following algorithm
for i = 1, N do
St1: y1[i] = a*y5[i−2];
St2: y2[i] = b*y6[i−1];
St3: y3[i] = x[i] + y1[i];
St4: y[i] = y2[i] + y3[1];
St5: y5[i] = y[i−2];
St6: y6[i] = y[i];
end.
The calculation period is L = 2, which means that a single couple of adder and multiplier can calculate it.
By the search of the space component the permissible coordinates Ksi are set:
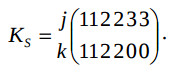
Here coordinates k = 0, 1, 2 mean multiplication, addition, equality operators. The matrix DS is derived from the equation
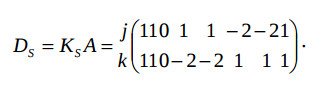
When the time component of the mapping is searched, the known coordinates are set in the weighted vectors-edges DT6 =(−2 0)sup>T and DT7 = (−1 0)T. The timing function is selected R=(L 1)=(2 1). To minimize the register number the vectors DTj, which leave the nodes 1,…,4 must have the coordinates providing R ⋅ DTj = 1 or 2, i.e. (0 1)Т, (1 −1)Т, or (1 0)Т, which provide the monotony condition.
To provide the injection condition, the vectors KTi with equal coordinate q must be different, for example, when KT1 = (X 0)T, or (X 1)T, then KT2 = (X 1)T, or (X 0)T where X is unknown value. The coordinates q of the vectors DTj are derived from the set of equations:
DT = KT A;
DT1 + DT3 + DT4 + DT6 = 0;
DT2 + DT5 + DT7 = 0.
Due to these conditions the following solution is found:

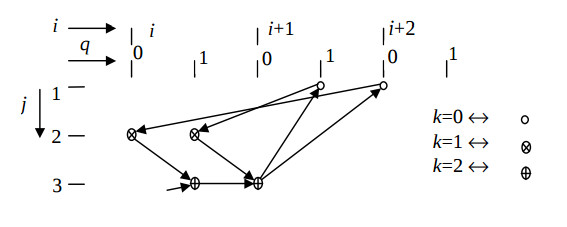
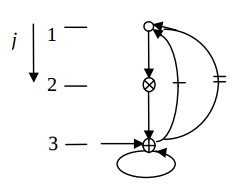
Fig.4 illustrates the derived algorithm configuration, and the Fig.5 does the respective structure configuration. This solution is distinguished by maximum hardware loading of the PUs and operation in the pipelined mode. It is the only structural solution of the second order IIR filter, in which the minimum clock cycle is equal to a single multiplier delay, and the input data run with the period of two cycles.
V. CONCLUSION
A method of application specific processor design is proposed which is based on the tensor theory of the system design. Its expansion was proven and widely used in the successive development of a set of DSP applications configured in the FPGAs, for example, published in [9, 10].
REFERENCES
[1] J.Isoaho, J.Pasanen, O.Vainio “DSP Sytem Integration and Prototyping With FPGAs” J. of VLSI Signal Processing. V 6, 1993, pp. 155-172.
[2] “System Generator for DSP. Getting Started Guide” August, 2007, 85p. See http://www.xilinx.com
[3] S.V.Rajopadhye “Synthesizing systolic arrays with control signals from recurrence equations” Distributed Computing. V3, 1989, pp. 88-105.
[4] J.Fortes, D.Moldovan “Data broadcasting in linearly scheduled array processors” Proc. 11 th Annual Symp. on Comp. Arch., 1984, pp. 224-231.
[5] S.Y.Kung “VLSI Array Processors” Eigenwood Cliffs, N.J.: Prentice Hall, 1988.
[6] S.Ritz, M.Pankert, and H.Meyr “Optimum vectorization of scalable synchronous dataflow graphs” Proc. Int. Conf. on Application Specific Array Processors. October. 1993.
[7] G.Kron “Tensor analysis of networks” MacDonald, London, 1965. 635 p.
[8 ] A. Sergyienko, O. Maslennikov. “Implementation of Givens QR Decomposition in FPGA” Lecture Notes in Computer Science, Springer, 2002, Vol. 2328, pp. 453-459.
[9] A. Sergyienko, V.Simoneko “DSP algorithm mapping into FPGAs” Proc. Int. Conf. Simulation-2006. Kiev. Energy Problem Modeling Institute of NAS of Ukraine. 2006. pp.189-193.
[10] O.Maslennikov, Ju. Shevtshenko, A. Sergiуenko “Configurable Microprocessor Array for DSP Applications” Lecture Notes in Computer Science. V. 3019. 2004. pp. 36-41.