Аналіз цифрових фільтрів за допомогою VHDL. Фазові та маскуючі фільтри.
А. М. СЕРГІЄНКО
z-перетворення і передаточна функція
z-перетворення широко використовується у цифровій обробці сигналів (ЦОС) через те, що сигнал виду x(n) = zn є власною функцією для лінійної системи, яка інваріантна до зсуву. Те, що функція є власною для системи, означає, що після обробки сигналу, який має форму цієї функції, одержимо сигнал, який має таку саму форму, але затриманий у часі та має іншу амплітуду. Покажемо, що zn є власною функцією для системи, що описується імпульсною реакцією h(k). Якщо такий сигнал подати на вхід системи, то одержимо, згідно з властивостями лінійної системи інваріантної до зсуву, вихідний (первинний) сигнал
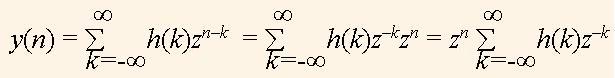 (1)
(1)
Отже, бачимо, що функція zn пройшла незмінною на вихід системи. Згідно з (1), передаточна функція системи дорівнює
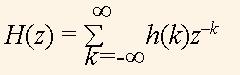 (2)
(2)
Так само, як і z, функція H(z) є комплексною функцією з амплітудою |H(z)| та фазою arg(H(z)). Функція H(z) має дві множини особливих точок. Перша множина – це такі точки q1,…,qM, для яких |H(qі)| = 0 і тому називаються нулями функції H(z). Друга множина – це такі точки r1,…,rN, для яких |H(rі)| = ∞ і тому вони називаються полюсами, функції H(z).
Щоб знайти нулі та полюси H(z), вираз (2) перетворюють у дріб з позитивними степенями при z. Якщо M – N = L, то чисельник H(z) помножують на zМ,а знаменник – на zN. Після цього одержують дріб
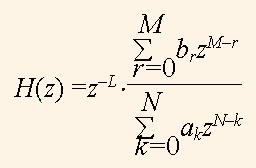 (3)
(3)
чисельник та знаменник якого представлені поліномами з позитивними ступенями при z, де pa0 = 1, множник z–L представляє собою затримку на L тактів і, як правило, може бути усунений з розгляду. Ці поліноми прирівнюють до нуля та знаходять корені цих рівнянь q1,…,qM та r1,…,rN, відповідно. Маючи множини нулів та полюсів, функцію H(z) можна виразити через них за допомогою формули
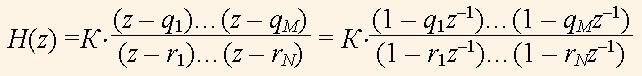 (4)
(4)
де К – коефіцієнт підсилення системи. Отже, множини нулів та полюсів визначають передаточну функцію системи.
Нулі та полюси передаточної функції
Графічно нулі та полюси зображають як точки на комплексній площині у вигляді кружечків та хрестиків, відповідно. На рис. 1 показано приклад розміщення нулів та полюсів деякого фільтра нижніх частот. Нуль чи полюс, як корінь рівняння, знаходять як пару реального та уявного чисел: r = rR + jrI . Для зручності корінь представляють у полярних координатах парою амплітуди |r| та фази ω: r = |r|е–jω. При цьому фаза ω відповідає певній частоті сигнала чи передаточної функції. Амплітуда полюса, як правило, не перевищує одиниці, тобто |r| < 1 , а кількість полюсів з ненульовими уявними координатами завжди парна.
Амплітудно-частотна характеристика
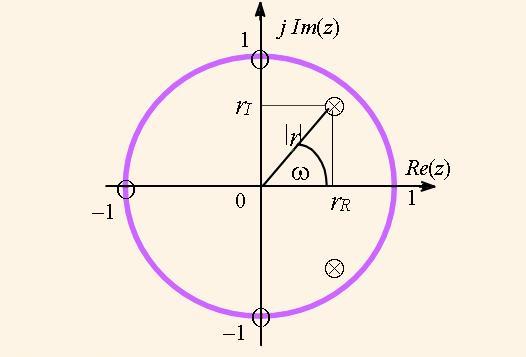
Модуль передаточної функції |H(z)| у тривимірному просторі можна представити як нескінченну мембрану, що пружно розтягується, яка натягнута над комплексною площиною на одиничній висоті. Точки мембрани, які відповідають нулям функції, притягнуті до комплексної площини, а точки, що означають полюси, відтягнуті вгору до нескінченності. Якщо на мембрані зобразити концентричні кола, то після її деформації згідно з розміщенням нулів та полюсів як на рис. 1, одержимо зображення, як на рис. 2. Товста лінія на поверхні |H(z)| (рис. 2) відображається на комплексну площину як коло з одиничним радіусом. Вона будується при
![]() (5)
(5)
При підстановці послідовності е-jω в H(z) одержимо дискретне перетворення Фур’є, а при підстановці в (2) чи (3) – передаточну функцію
|H(ω)| = |H(е-jω)|, (6)
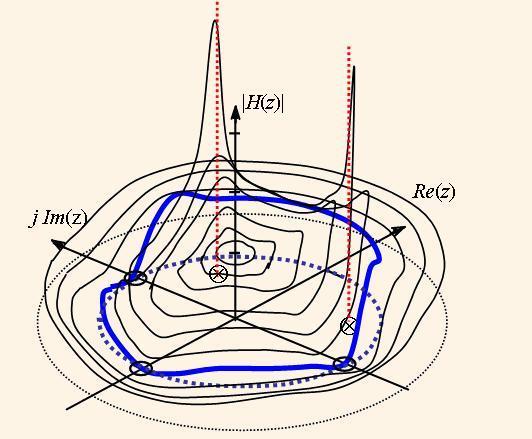
тобто залежність коефіцієнту передачі системи від частоти ω. Цю функцію називають амплітудно-частотною характеристикою (АЧХ) системи. При цьому крива, яка на рис. 2 розміщена на циліндрі одиничного радіуса з віссю о|H(z)|, розкручується на площині графіка АЧХ у вигляді безкінечної періодичної кривої з періодом 2π, як на рис. 3.
Для зручності вісь частот графіка АЧХ нормують, поділивши аргумент на 2π, тому одиниця на цій осі відповідає частоті дискретизації сигналу. Аналогічно АЧХ, обчислюють фазо-частотну функцію (ФЧХ) системи
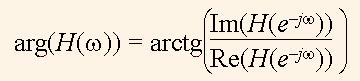
(7)
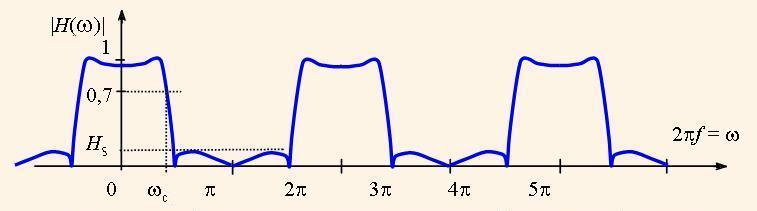
Для АЧХ цифрових фільтрів домовлено, що у смузі пропускання АЧХ має рівень не нижче √0,5 ≈ 0,7. Це означає, що у цій смузі потужність фільтрованого сигналу не знижується менше за рівень 0,5 від номінальної потужності. Відповідна частота межі смуги називається частотою зрізу (ωзр на рис. 3). Максимальний рівень фільтрованого сигналу у смузі непропускання називається рівнем придушення фільтру (Нпр на рис. 3).
Через те, що більшість систем ЦОС є системами з послідовно з’єднаних блоків, стало зручним представляти АЧХ у логарифмічному масштабі, тобто H(ω) = 20*lg|H(е–jωn)|. Тоді результуюча АЧХ системи дорівнює сумі АЧХ її складових. При цьому відлік рівнів АЧХ ведуть у децибелах. Наприклад, рівню 1 відповідає 0 дб, рівню 0,7 –рівень 3 дб., рівню 0,1 – рівень 20 дб.
Фазові фільтри
Далі будуть досліджуватись характеристики передаточної функції
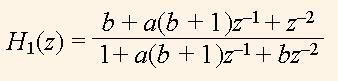
(8)
та інших передаточних функцій на її основі. H1(z) відповідає фазовому фільтру, нулі та полюси якого показані на рис. 4. Нулі та полюси функції (8) мають однаковий кут ω. Якщо модуль її полюса r, то модуль нуля дорівнює оберненій величині, тобто 1/r. В результаті цього нулі повністю компенсують вплив полюсів і тому АЧХ дорівнює 1 у всьому діапазоні частот.
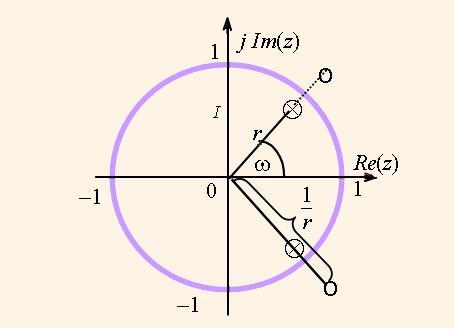
Положення полюсів та нулів визначається коефіцієнтами a,b, причому
a = – cos(ω); b = r2. (9)
Фазовий фільтр не змінює амплітуди сигналу, але спотворює його фазу. Причому, чим ближче параметр b до одиниці, тим різкіше спотворення фази на частоті ω. Якщо з’єднати паралельно два фазових фільтра з характеристиками H1(z), H2(z), тобто:
H3(z) =(H1(z) + H2(z))/2, (10)
то в їх загальній передаточній характеристиці H3(z) нулі перестають компенсувати полюси. Обидва канали H1(z), H2(z) пропускають два сигнали без зміни їх амплітуд. Але на частотах, де різниця фаз дорівнює π, 3π,…, сигнали компенсують один одного і результуючий сигнал є нульовим. Навпаки, на частотах, де різниця фаз 0,2π, 4π,…, цей сигнал залишається без змін. Завдяки цьому, в результуючій АЧХ |H(ω)| з’являються смуги пропускання та непропускання.
Фільтри з кратними затримками та маскуючі фільтри
У будь-якій лінійній системі, що інваріантна до зсуву, можна збільшити кожну затримку в k разів. Тоді замість передаточної функції H(z) розглядається функція з кратними затримками H(zk). Ефект такого збільшення затримок полягає в тому, що масштаб графіків АЧХ, ФЧХ вздовж осі частот зменшується у k разів.
Нехай k=2, тоді на графіку на рис. 3 слід замінити відліки π на π/2, 2π на π і т.д. В результаті, кількість смуг пропускання та непропускання в частотній області, що розглядається, подвоюється.
Нехай маємо H4(z) = H3(zk). Якщо АЧХ |H4(ω)| має кілька смуг пропускання, то робочу смугу можна виділити за допомогою маскуючого фільтра HМ(z), який з’єднаний послідовно з фільтром, що реалізує H4(z). Тобто результуюча функція
H(z) = H4(z)*HМ(z). (11)
Для цього АЧХ маскуючого фільтра повинна мати смуги непропускання у тих діапазонах частот, де знаходяться смуги пропускання в АЧХ |H4(ω)|, які необхідно придушити.
VHDL-функції для аналізу передаточних функцій
Для обчислення передаточних функцій слід використати пакети IEEE.MATH_REAL та IEEE.MATH_COMPLEX. В останньому пакеті визначені типи, константи та функції, які оперують з комплексними даними.
Для обчислення передаточних функцій розроблено ряд функцій з використанням пакетів IEEE.MATH_REAL та IEEE.MATH_COMPLEX. Обчислення послідовності zn виконується з використанням наступних функцій, які перезавантажують одна одну
--число Z радиусом MAG в степени угла j*fі
function Z(mag,fi:real) return COMPLEX_POLAR is
begin
return mag*exp(COMPLEX_TO_POLAR(MATH_CBASE_J)*(fi));
end Z;
--число Z радиусом 1 в степени угла j*fі
function Z(fi:real) return COMPLEX_POLAR is
begin
return exp(COMPLEX_TO_POLAR(MATH_CBASE_J)*(fi));
end Z;
Наступна функція обчислює H1(z) за формулою (8), але для позитивних степенів z, тобто з урахуванням (3). Вона необхідна для сканування простору |H1(z)| при пошуку нулів та полюсів, коли встановлюється різна величина mag амплітуди та фази fi комплексного вектора z. Також вона використовується для розрахунків АЧХ та ФЧХ.
обчислює (bZ^2+а(b+1)Z+1)/(Z^2+c(b+1)Z+b)
function Allpass2(b,a: real; --коэффициенты
mag, fi: real) -- амплитуда, угол для z
return COMPLEX_POLAR is variable tn,td: COMPLEX_POLAR;
begin
td:=COMPLEX_TO_POLAR(COMPLEX'(b,0.0))
+a*(b+1.0)*Z(mag,fi) + Z(mag**2,2.0*fi);
tn:=COMPLEX_TO_POLAR(COMPLEX'(1.0,0.0))
+a*(b+1.0)*Z(mag,fi) + b*Z(mag**2,2.0*fi);
return tn/td ;
end Allpass2;
Наступна функція обчислює H1(z2) (8) для від’ємних степенів z з одиничною амплітудою, тобто вона обчислює H1(ω), де ω = fi . Тому вона використовується лише для розрахунків АЧХ та ФЧХ.
function Allpass2x2(b,c:real; fi:real) return COMPLEX_POLAR is variable tn,td: COMPLEX_POLAR; begin tn:=COMPLEX_TO_POLAR(COMPLEX'(b,0.0)) +c*(b+1.0)*Z(-2.0*fi) + Z(-4.0*fi); td:=COMPLEX_TO_POLAR(COMPLEX'(1.0,0.0)) +c*(b+1.0)*Z(-2.0*fi) + b*Z(-4.0*fi); return tn/td ; end Allpass2x2;
Для сканування простору |H1(z)| використовується наступний фрагмент VHDL-програми.
signal clk:bit;
signal m,ph:real:=0.0;
signal a,b,logm,phase,mag:real:=0.0;
begin
clk<=not clk after 5ns; --генератор синхросигналов
process(CLK)
variable p,phas:real:=0.0;
variable Hz: COMPLEX_POLAR;
begin
a<=-0.5; b<=0.64; -- параметры H(z)
if clk='1' and clk'event then
phas:= phas+0.001; -- счетчик фазы (частоты)
p:=phas*MATH_PI*2.0; -- нормированная фаза
m<= trunc(phas)*0.1+0.1; -- амплитуда Z
ph<=phas; -- сигнал фазы
end if;
Hz:=Allpass2(b,a,m,p); --собственно H(z)
mag<=abs(Hz); -- амплитуда H(z)
phase<=Hz.ARG; -- фаза H(z)
logm<=20.0*log10(abs(Hz)); -- H(z) в децибелах
end process;
Дослідження фазових фільтрів за допомогою VHDL
Дослідимо функцію H1(z) за допомогою програми на VHDL, яка будує графіки |H1(z)| для різних значень |z| щоби експериментально визначити положення нулів та полюсів функції (8). Нехай задано a = –0.5, b = 0.64. Тоді
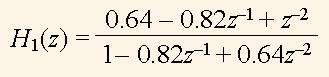
(12)
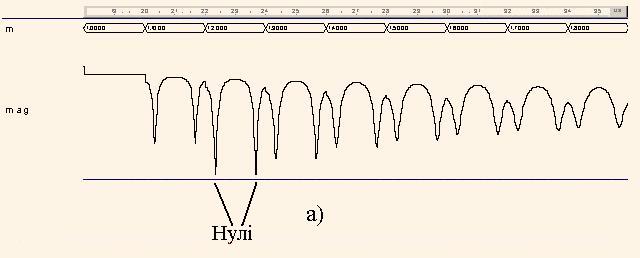
Після запуску програми на моделювання у системі Aldec ActiveHDL одержано графік |H1(z)| (рис. 5), у якому на кількох інтервалах, позначених m, розміщено криві |H1(m,ph)|, де m – довжина (причому m = 0.1, 0.2,…), ph – нормований кут (фаза, частота) вектора z, повний оберт вектора z відбувається коли ph – ціле число. Перша половина |H1(m,ph)| – для m = 0.1,...0.9, а друга половина – для m = 1.0,...1.9. Таким чином, кожен інтервал відповідає замкненій кривій, як на рис. 4. Там же аналогічно показано графік arg(H1(z)) для m = 0.6,...1.1.
Аналіз графіків на рис. 5 показує, що полюси функції H1(z) мають фазу ± 2π*ph = ± 2π*0.1645 = ± 1.0336 і знаходяться в точках r1 = 0.8 ∠1.0336 та r2 = 0.8 ∠–1.0336. Нулі функції H1(z) мають таку саму фазу і дорівнюють q1 = 1.3 ∠1.0336, q2 = 1.3∠–1.0336. Слід відмітити, що –cos(1.0336) = –0.512 ≈ а, 1/0.8 = = 1.25 ≈ 1.3 та 0.82 = 0.64 = b, тобто справджуються відношення (9).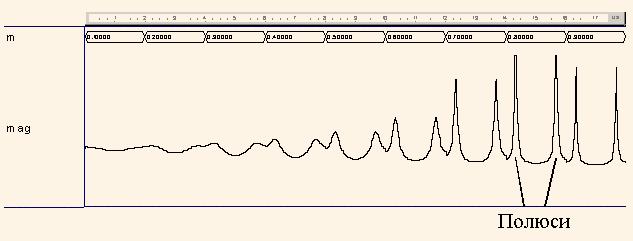
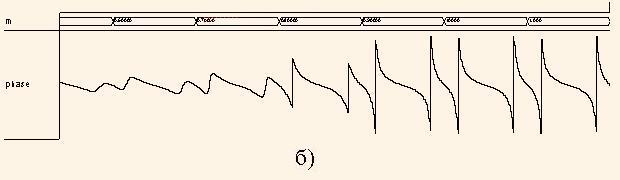
Аналіз графіка arg(H1(z)) показує, що при куті ph = 0 фаза дорівнює 0, при поступовому збільшенні ph фаза плавно зменшується. Але якщо ph наближається до положення полюсів, фаза стрімко досягає значення ±π.
Тепер проаналізуємо функцію H3(z) при H2(z) = z–1 . Для обчислення |H3(ω)| у попередній програмі один оператор присвоювання змінній замінюється на наступний оператор, що відповідає формулі (10) .
Hz:=(Allpass2(b,a,1.0,p)+Z(-1.0*p))/2.0 (13)
Тут H2(z) = z–1 – теж передаточна функція фазового фільтра, тому |H3(z)| = 1 для усіх z. Зробимо також корекцію коефіцієнта b = 0.625, тобто,
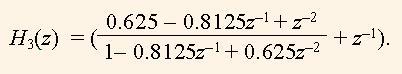
(14)
Слід наголосити, що множення на коефіцієнт 0.625 можна виконати як одне додавання множеного, яке зсунуте на один та три розряди вправо. Аналогічно можна виконати множення на 0.8125. Це суттєво спрощує апаратну реалізацію фільтра, який відповідає цій передаточній функції.
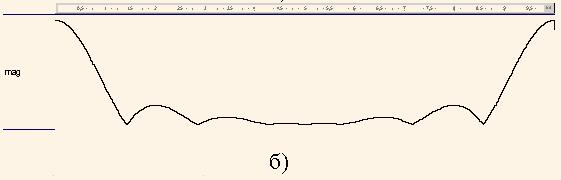
Після запуску програми на моделювання одержано графіки |H3(ω)| та arg(H3(ω)) (рис. 6) для частот ω=(0, 2π) або для нормованих частот ph = (0, 1). Як бачимо, додавання передаточної функції H2(z) створює АЧХ фільтра нижніх частот з частотою зрізу fзр = 0,156 ≈ arg(r1) =1/(2π) 1,0336 = 0,164 від частоти дискретизації. Виміряний за графіком logm рівень придушення складає 8.5 дб.
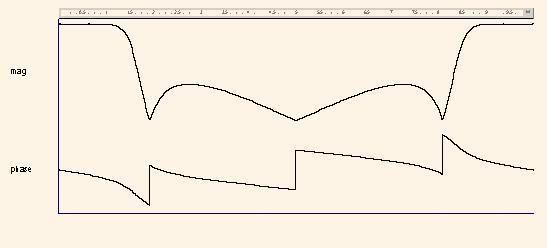
Тепер дослідимо функцію H4(z):
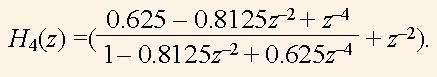
(15)
Так само, як і у попередньому випадку, графік |H4(ω)| (рис.7,а) будується за допомогою заміни оператора на наступний оператор
Hz:=(Allpass2x2(b,a,p)+Z(-2.0*p))/2.0;
Функцію
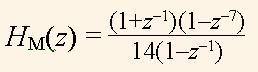
(16)
дослідимо за допомогою графіка |HМ(ω)| (рис.7,б), який будується за оператором
Hz:=(COMPLEX_TO_POLAR(COMPLEX'(1.0,0.0))+Z(-p))
*(COMPLEX_TO_POLAR(COMPLEX'(1.0,0.0))-Z(-7.0*p))/
(COMPLEX_TO_POLAR(COMPLEX'(1.0,0.0))-Z(-p))/14.0;
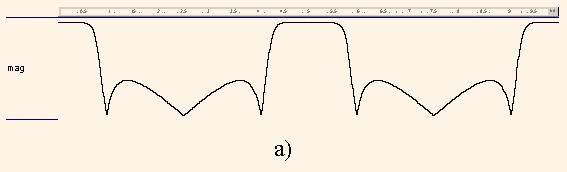
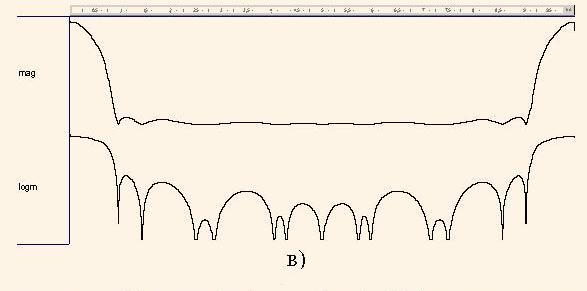
Видно, що цей графік представляє собою повторений двічі графік на рис.6, що є характерним для передаточних функцій з кратними затримками.
Нарешті, дослідимо функцію (11), яка є композицією функцій H4(z) та HM(z):
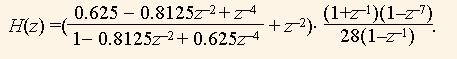
(17)
Графік результуючої АЧХ |H(ω)| (рис.7,в) будується за допомогою оператора
Hz:=(Allpass2x2(b,a,p)+Z(-2.0*p))*COMPLEX_TO_POLAR(COMPLEX'(1.0,0.0))+Z(-p)
*COMPLEX_TO_POLAR(COMPLEX'(1.0,0.0))-Z(-7.0*p))/
(COMPLEX_TO_POLAR(COMPLEX'(1.0,0.0))-Z(-p))/28.0;
Як слідує з рис. 7, функція HМ(z) маскує H4(z), в результаті чого одержано передаточну функцію H(z) (2) фільтра нижніх частот з частотою зрізу fзр = 0,06 від частоти дискретизації та рівнем придушення більше за 23 дб.
Отже, доволі проста передаточна функція (17), яка може бути реалізована без використання множень, має досить високі фільтруючі властивості. Аналогічний фільтр зі скінченною імпульсною характеристикою повинен бути принаймні п'ятдесятого порядку.
З літератури, що вказана нижче, можна дізнатись більше про фазові, маскуючі фільтри, та фільтри з кратними затримками.
Література
1. Chung J. G., Parhi K. K. Pipelined wave digital filter design for narrow-band sharp-transition digital filters // Proc. IEEE Workshop VLSI Signal Processing, La Jolla, CA. –1994. –Р. 501-510.
2. Regalia P., Mitra S.K., Vaidyanathan P.P. The Digital All-Pass Filter: A Versatile Signal Processing Building Block // Proc. IEEE. –1988. –V.76. –№1. – p.19-37.