Моделі генераторів сигналів та їх обробка на VHDL
А.М. СЕРГІЄНКО
У цій статті пропонується розглянути прості моделі генераторів цифрових сигналів, прості, але ефективні алгоритми обробки сигналів, а також зробити з ними ряд дослідів.
Різноманітні генератори сигналів використовуються для діагностування, тестування та налагодження алгоритмів і пристроїв цифрової обробки сигналів (ЦОС). Часто використовується генератор синусоїдальних сигналів через те, що такий сигнал проходить через лінійну систему без зміни своєї форми. Приклад такого генератора пропонується тут http://kanyevsky.kpi.ua/wp-content/uploads/2017/09/labexercise-1.pdf. Шумовий сигнал має широкий спектр і тому дослідження його проходження через лінійну систему дає змогу оцінити її частотні характеристики. Також шум додається до сигналу, щоб виявити фільтрувальні властивості системи. Пропускаючи через систему сигнал спеціальної форми, можна перевірити її якість, так як система з гідною передаточною характеристикою зберігає форму сигналу.
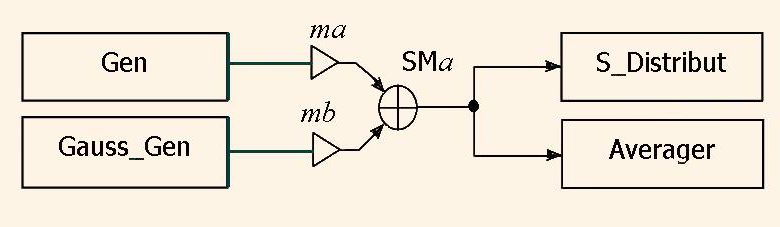
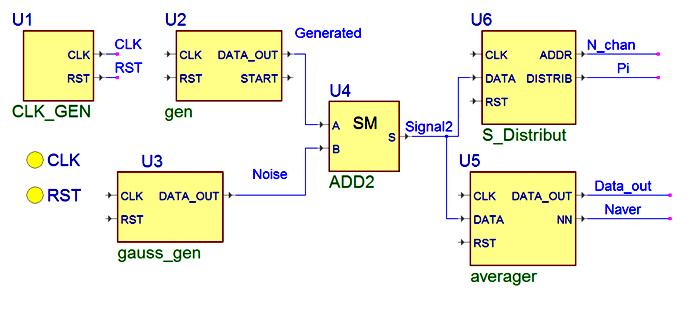
У статті розглядається побудова генератора сигналів спеціальної форми Gen і генератор гаусового шуму Gauss_Gen, та виконується з ними ряд дослідів, включивши його у схему на рис. 1.
Інші блоки схеми на рис.1. – це блок аналізу статистичного розподілення сигналу S_Distribut та блок усереднення сигналу Averager.
В основу генератора гаусового шуму покладено виконання центральної граничної теореми. Згідно з нею, якщо випадкова величина є сумою досить великого числа незалежних між собою доданків, кожен з яких є незначним за величиною, то ця сума має розподіл, який наближається до нормального.
На VHDL він виглядає наступним чином.
library IEEE;
use IEEE.STD_LOGIC_1164.all;
use IEEE.math_real.all;
entity Gauss_Gen is
generic(nn:natural:=1; --ступінь біноміального розподілу менше 16
m:REAL:=0.0 -- усереднене вихідне дане );
port( CLK : in STD_LOGIC; RST : in STD_LOGIC; DATA_OUT : out REAL:=0.0 );
end Gauss_Gen;
architecture Model of Gauss_Gen is type arri is array (0 to 15) of integer;
type arrr is array (0 to 15) of real;
begin SFR:process(clk,rst) variable s1:arri:=(3,33,333,3,4,5,6,7,8,9,11,22,33,others=>55);
variable s2:arri:=(5,55,555,50,6,7,8,9,5,6,7,21,33,others=>22);
variable r:arrr:=(others=>0.0);
variable s:real:=0.0;
begin
if rst='1' then
DATA_OUT<=0.0;
elsif clk='1' and clk'event then
s:=0.0;
for i in 0 to nn-1 loop -- nn генераторів шуму
UNIFORM (s1(i),s2(i),r(i));
s:=s+r(i);
end loop;
DATA_OUT <= 2.0*(s/real(nn)-0.5)+ m;
end if;
end process;
end Model;
Блок Gauss_Gen має дві частини: nn паралельних генераторів чисел з рівномірним розподілом та суматор, який додає nn згенерованих чисел. Генерація чисел з рівномірним розподілом в інтервалі [0.0,1.0] виконується за конгруентним алгоритмом з використанням процедури UNIFORM. Одержана сума ділиться на nn і видається як відлік шуму, який розподілено в інтервалі [-1.0,1.0]. Тут nn – це настроювальна константа. При nn = 1 генератор видає шум з рівномірним розподілом, при nn = 2 –з трикутним розподілом, а при nn > 10 – практично з гаусовим розподілом.
Сигнали від генераторів Gen та Gauss_Gen складаються у суматорі SM після множення на масштабні коефіцієнти mа, mb, відповідно. В результаті, одержуємо сигнал х(n), що досліджується. Модель суматора наступна.
library IEEE;
use IEEE.STD_LOGIC_1164.all;
entity ADD2 is
generic(ma:real:=1.0;
mb:real:=1.0);
port( A, B: in REAL;
S : out REAL:=0.0 );
end ADD2;
architecture ADD2 of ADD2 is
begin
S<=ma*A + mb*B;
end ADD2;
Статистичні властивості сигналу х(n) можна оцінити за допомогою побудови гістограми розподілу його вірогідності. Обчислення гістограми виконують наступним чином. Інтервал зміни величини х(n), наприклад, а < х(n) < b, ділять на k підінтервалів рівної довжини. і-му інтервалу, включаючи 0-й підінтервал х(n) < а та k+1 –й підінтервал b < х(n), ставиться у відповідність натуральне число Мі, яке дорівнює кількості відліків х(n), які попадають у відповідний підінтервал. Підінтервал часто називають інтервалом групування або кишенею.
Нехай ширина підінтервалу дорівнює с = (b – а)/k , а границя і-го інтервалу – di = a + i*c. Тоді після аналізу усієї послідовності х(n) у і-й кишені одержимо число таких х(n), що di-1 < х(n) < di. Виключеннями є 0-а кишеня з кількістю відліків х(n) < а та k+1 -а кишеня з числом таких х(n), що b < х(n).
При обробці х(n) на комп’ютері організують масив цілих чисел М розміром k+2. Якщо а < х(n) < b , то обчислюють номер кишені
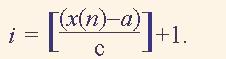 (1)
(1)
Тут дужки [ ] означають цілу частину числа. Одержавши індекс за формулою (1) у і-ту комірку, тобто кишеню М(і) додають 1.
Такі обчислення повторюють для усіх х(n).
На основі одержаних результатів можна для послідовності х(n) довжиною N обчислити вибіркову функцію щільності вірогідності за формулою
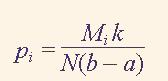 (2)
(2)
Вибір параметрів а, b, k залежить головним чином від уяви про розподіл сигналу х(n), способу збору даних та їх кількості. Напевне, що кількість кишень недоцільно вибирати більше за о√N чи за кількість рівнів квантування сигналу. Параметри а, b, k уточнюються після циклів пробної побудови гістограми.
Побудова гістограми виконується блоком S_Distribut :
library IEEE;
use IEEE.STD_LOGIC_1164.all;
entity S_Distribut is
generic(channels:natural:=100;
drange:real:=2.0;
dmin:real:=-1.0);
port(CLK, RST: in STD_LOGIC;
DATA : in REAL:=0.0;
ADDR : out INTEGER;
DISTRIB : out INTEGER);
end S_Distribut;
architecture MODEL of S_Distribut is
type Tarr is array (0 to channels+1) of natural;
signal Distr_arr:Tarr:=(others=>0);
signal addri,aa:natural;
signal even: STD_LOGIC;
begin
process(CLK)
variable addrw:integer;
begin
addrw:=integer(real(channels)*(DATA-dmin)/drange-0.5)+1;
if DATA> (dmin+drange) then
addrw:=channels+1;
elsif DATA<=dmin then
addrw:=0;
end if;
aa<=addrw;
if RST='1' then
Distr_arr<=(others=>0);
elsif CLK='1' and CLK'event then
Distr_arr(addrw)<=Distr_arr(addrw)+1;
end if;
end process;
process(CLK)
begin
if RST='1' then
addri<=0;
even<='0';
elsif CLK='1' and CLK'event then
if addri=channels+1 then
addri<=0;
even<=not even;
else
addri<=addri+1;
end if;
end if;
end process;
ADDR<=addri when even='1' else -1;
DISTRIB<=Distr_arr(ADDRi) when even='1' else -1;
end MODEL;
Він має настроювальні константи channels, тобто k, dmin, тобто а та drange, який дорівнює b – а.
Якщо сигнал х(n) – періодичний, то х(n+То) = х(n), де То – його період. Реальний сигнал х'(n) має додаткову складову у вигляді шумового сигналу q(n), тобто х'(n) = х(n) + q(n). Блок усереднення сигналу Averager описаний у наступній моделі.
library IEEE;
use IEEE.STD_LOGIC_1164.all;
entity Averager is
generic(N:integer:=300); -- Період усереднення
port( CLK, RST: in STD_LOGIC;
DATA : in real;
DATA_OUT : out real;
NN:out integer );
end Averager;
architecture beh of Averager is
type Tarr is array(0 to N-1) of real;
signal arr : Tarr:=(others=>0.0);
signal addr:natural;
signal NNi:natural:=1;
begin
process(CLK,RST) begin
if RST='1' then
arr<= (others=>0.0);
addr<=0;
NNi<=1;
elsif CLK='1' and CLK'event then
arr(addr)<= arr(addr)+DATA;
if addr = N-1 then
addr<=0;
NNi<=NNi+1;
else
addr<=(addr+1);
end if;
end if;
end process;
DATA_OUT<=arr(addr)/real(NNi);
NN<=NNi;
end beh;
Він виконує додавання періодів сигналу х'(n). Якщо шум q(n) є послідовністю випадкових чисел з нормальним законом розподілу, то після додавань N періодів сигналу х'(n) його складова q(n) збільшиться менше, ніж у N разів. Отже, після N додавань періодів сигналу х'(n) та нормалізації результату діленням на N для n = 0,…,То–1 та k = 0,…,NTo–1 одержимо результат
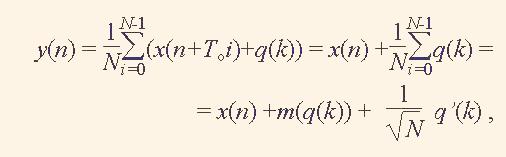 (3)
(3)
де m(q(k)) – математичне очікування шуму q(k), q’(k) – усереднений шумовий сигнал. Отже, бачимо, що усередненням сигналу можна знизити рівень шуму до √N разів. Тому усереднення періодичного сигналу часто використовується для його фільтрації від шуму. При цьому важливими умовами є прямування до нуля математичного очікування шуму та строга рівність довжини масиву y(n), де накопичується усереднений сигнал, періоду To сигналу х(n).
Нехай задано функцію

То = N1 + N2 . Тоді модуль, який її генерує, описується як наступний:
entity Gen is generic(n1:natural:=100; n2:natural:=200); port(CLK : in STD_LOGIC; RST : in STD_LOGIC; DATA_OUT : out REAL:=0.0; START : out BIT); end Gen; architecture MODEL of Gen is signal ct2:natural; begin process(CLK,RST) begin if RST='1' then ct2<=0; START<='1'; elsif CLK='1' and CLK'event then START<='0'; if ct2=n1+n2-1 then ct2<=0; else ct2<=ct2+1; end if; if ct2<=n1 and ct2>0 then DATA_OUT<= arctan(real(ct2)/real(n1)); else DATA_OUT<= cos(MATH_PI*real(ct2-n1)/real(n2)); end if; end if; end process; end MODEL;
Побудована схема стенду для іспитів показана на рис.2.
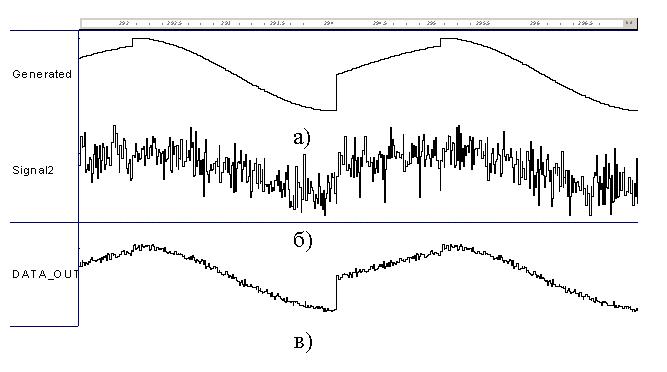
На рис. 3. показані графік сигналу, згенерованого модулем Gen, графік сигналу з доданим гаусовим шумом, амплітуда якого відноситься як 3:1 та сигнал після 100 циклів усереднення у модулі Averager. Аналіз графіків показує, що дійсно, після 100 усереднень періодичного сигналу рівень доданого гаусового шуму зменшується приблизно у 10 разів.
На рис. 4. показані графіки сигналів, одержаних на виході модуля S_Distribut для сигналів без шуму, з доданим шумом з рівнем 0,3 та рівнем 3. Графіки показують, що сигнал має позитивну постійну складову. Перший графік має форму, характерну для сигналу без шуму, другий графік показує наявність в сигналі шуму, а третій – що в сигналі переважає шум, причому саме шум з імовірно гаусовим розподілом.

Можливості використання VHDL для обробки сигналів показані у статті http://kanyevsky.kpi.ua/ru/%D1%81%D1%82%D0%B0%D1%82%D1%8C%D0%B8/vhdl-%D0%BF%D1%80%D0%BE%D1%82%D0%B8%D0%B2-matlab/ . В даній статті продовжено викладання цього досвіду і черговий раз показано, що мова VHDL має широкі можливості для вирішення задач моделювання у різноманітних галузях.