FPGA Implementation of the Conjugate Gradient Method
FPGA Implementation of the Conjugate Gradient Method
Oleg Maslennikov,
Technical University of Koszalin, ul.Partyzanow 17, 75-411 Koszalin, Poland, Email: oleg@moskit.ie.tu.koszalin.pl
Volodymir Lepekha, Anatoli Sergyienko,
National Technical University of Ukraine “KPI”, Kiev, Ukraine, Email: aser@comsys.kpi.ua
Oleg Maslennikov,
Technical University of Koszalin, Poland, Email: oleg@moskit.ie.tu.koszalin.pl
Abstract
The rational fraction number system is proposed to solve the algebraic problems in FPGA devices. Such a number consists of the n-bit numerator and n-bit denominator, and can represent numbers with 2n bit mantissa. Experimental linear equation system solver was developed in FPGA device, which implements the recursive conjugate gradient method. Its hardware arithmetic unit can calculate addition, multiplication, and division of rational fractions with n=35 in pipelined mode. The computer solves the strip matrices with the dimensions more than 1000.
1. Introduction
Field programmable gate array (FPGA) is considered to be an excellent computational raw for hardwired applications in digital signal processing (DSP), communications, control, multimedia data computing, etc. Modern FPGA devices provide millions configurable gates, and millions bits of built in memories, which can operate at the frequencies up to hundreads of MHz. FPGA plattforms, which intended for DSP applications, provide tenths and hundreads of islands, each of them has hardware multiplier and long product accumulator. As a result, such an FPGA calculator has the peak throughput more than 100 billion operations per second.
Linear algebra problem solving becomes the important task of the modern DSP applications. They are adaptive filtering, curve interpolation, system parameter estimation, signal back propagation problem solving, rigid body dynamic modelling, image improvement and others.
Such problem solving affords high precision calculations. Therefore it is usually implemented using single and double precision floating point numbers. That is why linear algebra problems are usually solved only in PC and floating point DSP microprocessors. Such calculations are made in usulal DSP microprocessors very rare, and solve very small problems (matrix dimensions are usually not higer than 10) because of their fixed point ALU.
Modern high volume FPGAs give the opportunity to build the highly pipelined floating point ALUs with double precision, such as described in [1], [2]. The disadvantages of such ALUs are comparatively high hardware volume and pipelining delays. For these disadvantages such FPGA processors hardly compete with the widely used floating point microprocessors both in speed and in cost.
FPGAs can provide the very precise fixed point number representation up to hundreads of bits. But till now the efforts to solve the linear algebra problems in FPGA are very rare. Really, long word adders can add and substract large integers very quckly in them. The high speed of them can be supported by pipelining. But hardware multipliers for such long words occupy much of chip place. For example, 64 to 64 bit multiplier is buitlt on sixteen 16 to 16 bit hardware multiply units.
In the usual DSP algorithms the division operation is very rare. On the contrary, in the linear algebra algorithms the division is frequently used operation. Moreover, this operation is the source of large calculation errors. The hardware dividers are much complex than multipliers in modern FPGA, because such an n-bit divider consists of n adder-substractor stages. Therefore some efforts were made to use the integer numbers for linear algebra problem solving, which are based on the division free algorithms. An example is shown in [3], where the Givens QR-decomposition algorithm, which is based on rotations, was implemented in FPGA.
Among many linear algebra methods and algorithms the conjugation gradient method is famous for its features like minimum operation number during the sparce matrice solving, full convergention to the exact solution for less than n iterations, where n is the matrix dimension. Besides this method uses mostly the convolution operation, vector multiply and add, like in usual DSP algorithms. It needs less than 2n division operations and none operation like square root. But the most disadvantage of this method consists in that, that its termination is guaranteed only if all the calculations are implemented without errors. Therefore this method is used rarely because floating point operations do not provide the needed precision [4]. If the precision problem is solved than this method would be very useful for many DSP applications.
In the representation the rational fraction number system is proposed to implement the conjugate gradient method in FPGAs. Such a system was already used in the configurable DSP processor, represented in [5], where the example of the Toeplitz matrix problem solving was shown. Then the FPGA processor is described which solves linear equation systems with sparce matrices. The processor behavioral model description was shown, which has provided the dependency search between the problem dimension and needed data bit widths. The processor was configured in FPGA, and showed its high effectiveness.
2. Fraction number calculations
Fraction number is the numerical object which consists of integer numerator and integer denominator. Its name proves that such fraction represents any rational number. Rational numbers are the real numbers which are derived as linear equation solutions, or integer polynome divisions.
Rational fraction a/b has the feature, that it can approximate the given irrational or transcendental number x. If the fraction a/b is less than x, and fraction c/d is higher than x, then the fraction (a+c)/(b+d), named medianta, is nearest to x than that fractions. Therefore if a set of mediantes is built then we can to approximate the number x with any precision.
If the uninteger number x is represented by 2n digits with the error ξ1, then it can be represented by the fraction a/b with the error ξ2 ≈ ξ1, and the numbers a and b have no more than n digits in their representation [5]. The fraction number representation has a set advantages. Firstly, any binary fraction is depended on the binary data representation, and not exactly represents the real number. The floating point number in binary representation is equal to the fraction, which denominator is the power of two, and it is not equal to the respective decimal fraction because it has the denominator which is equal to power of ten. For example, the number 1/9 =1/10012 is the exact fraction in any numeric system, and can be represented with error as the decimal fraction 0.1111 or binary fraction 0.111000111000112 .
Secondly, the rational fractions help to find the irrational or transcendental number approximation with the given precision. Many elementar functions are effectively calculated by proper rational approximation formulas. Many constants and constant tables are effectively stored as rational numbers.
And thirdly, rational fractions provide comparatively simple set of arithmetical operations. The multiplication a/b to c/d and division of them are equal to aс/(bd), and bd/(aс), respectively. Note, that the division of the numerator to the denominator is not calculated. Addition of them is equal to (ad+bc)/(bd). For comparison of two numbers it is enough to calculate ad-bc.
Comparing the operation complexity one have to take into account that the numerator and denominator bit number is more than in two times less than the bit number of integers which provide the equal precision. Therefore, the hardware complexity of the fraction adder is near the complexity of the integer multiplier with the same precision, and the fraction multiplier complexity is in two times less than the integer multiplier complexity.
In seventies the main hardware implemented operation in mini – and microcomputers was addition. The floating point operations were implemented as subprograms which lasted for a lot of clock cycles. To speed up the calculations in that time the rational fractions were proposed to substitute the floating point numbers. The main disadvantage of rational fractions is that the bit number increases dramatically when operations are implemented precisely. Therefore to minimize this increase the division of numerator and denominator to their greatest common divisor was made, as in the fraction processor which was proposed in [6]. But when the floating point coprocessors became widely used, the fractional number processors became out of sight.
Then the rational fractions were built in many mathematical CAD tools like Maple which are implemented in PC. Such fractions are widely used to do calculations with unlimited precision, to solve modern criptographical problems and others. Therefore such languages as PERL and Java are supported by packages providing unlimited precision calculations. For this purpose in [7] a new standard of data representation is proposed, named composite dates. These dates among integers and reals include rational fractions as well.
To solve many mathematical problems the high precision arithmetical are needed. For example, the linear equation systems with sparce matrices is effectively solved by the conjugate gradient method. But the only disadvantage of this method consists in that that its convergention is assured when all the calculations are made precisely [4]. Therefore this method could not be implemented when the single precision floating point is used.
Note, that all the floating point DSP microprocessors have the built in single precision floating point, and could not calculate the double precision floating point numbers effectively. Therefore they are rarely used to solve the linear algebra problems. In this situation the rational fraction calculations can have the high effectiveness. Below the rational fraction effectiveness for the conjugate gradient method implementation is shown.
3. Conjugate gradient method modeling
To prove the rational fraction number effectiveness the linear equation solving by the conjugate gradient method was modelled using VHDL simulator. Firstly, the package Fract_lib was designed in which the type of fraction FRACTV was declared. The object of this type consists of two bit vectors of the length m. In that package the functions of addition, subtraction, multiplication and division of fractions are described which overload the respective operations of the VHDL language. The type ARRAYFR1 represents the vector of fractions, the constant NIL represents the zeroed fraction, the function FRACT_REAL translates the fraction into the real number.
Then the VHDL program was designed, which loads the initial dates and solves the linear equation system. The diagonal matrix A of the system is symmetric, positively defined one, and is represented by the arrays a0, a1, a2 of its diagonals. The left column of the system, and unknowns are represented by the vectors b, and x. The multiplication of the matrix A to the column p is implemented in the procedure MATR_x_VECT. The conjugate gradient method is implemented in the following process.
process
variable k:natural:=0;
variable x,r,p,w:ARRAYFR1(1 to n);
variable pap,eps1,alpha,beta:FRACTV;
begin
wait for 1 ns;
xf:=(others=>NIL); r:=b; epsi:=NIL;
for i in r'range loop
eps1:=eps1+r(i)*r(i);
end loop;
loop
k:=k+1;
if k=1 then
p:=r;
else
beta:=eps1/eps2;
for i in p'range loop
p(i):=r(i)+beta*p(i);
end loop;
end if;
MATR_x_VECT(a0,a1,a2,p,w);
pap:=NIL;
for i in p'range loop
pap:=pap+p(i)*w(i);
end loop;
alpha:=eps1/pap; eps2<=eps1;
eps1:=NIL;
for i in x'range loop
x(i):=x(i)+alpha*p(i);
r(i):=r(i)-alpha*w(i);
eps1:=eps1+r(i)*r(i);
x(i)<=FRACT_REAL(x(i));
end loop;
sqe<=(SQRT(FRACT_REAL(eps1)/real(n)));
wait on clk;
exit when sqe<1.0e-4;
end loop;
report "End of calculation" severity failure;
end process;
This process is similar to the algorithm which is represented in [4]. All the dates are represented by m bit fractions, and the resulting vector x is the vector of reals. The array A is constant one, and the array b is randomized one. When the process is running for the first nanosecond the input dates are initialized, then with each clock edge one iteration of the algorithm is calculated. The calculations are stopped when the quadratic mean error sqe is less than the given threshold. To control the results the similar process is running but with the double precision real dates.
The results of the modelling is the dependence between the fraction bit number m and the maximum array length n when the convergention process is stable. The derived dependence is shown on the fig.1.
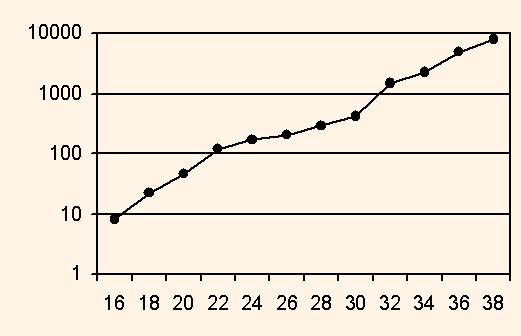
Analysis of this dependence shows the following rule of thumb: each 2 digit data width increase provides the twofold increase of the maximum problem dimension. Extrapolating of the dependence line shows that the data width 52 and 64 can provide the solving the problem of dimension 1 mln. and 60 mln. respectively. The given threshold of the number sqe provides 4-5 true decimal digits of the result, which is enough for most of DSP applications.
4. Processor for solving of sparse matrix equations
To prove the effectiveness of the conjugate gradient method calculations using rational fractions the FPGA – based processor was designed. The processor consists of pipelined arithmetic unit (AU), memory blocks and control unit which generates proper address sequences.
The algorithm calculations are based on vector multiplication and addition of weighted vectors. Therefore the base operation is multiplication and addition of data streams: P = AX+Y. The AU structure is shown on the fig.2.
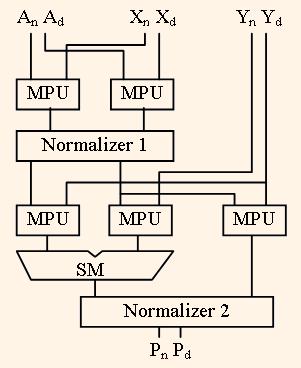
Here the indexes n and d sign the numerator and denominator of the fraction. The processor is implemented in the Xilinx Virtex2-Pro XC2VP4 device, which has built in 18 bit width multiply units and 18 kilobit dual port RAMs.
The fraction bit width was selected which is equal to 35. This bit width provides the maximum problem size 3500. But the memory size of the selected FPGA device provides maximum vector length 1024. The samples in the matrix A are represented by 18 bit integers. When this matrix is multiplied then these integers are expanded to full 35 bits of numerators and 35 bits of denominators. In such a manner the needed memory volume is minimized.
Each multiplier MPU consists of four multiply units and three adder stages. Normalizer shifts left both numerator and denominator of operation result to the equal bit number to prevent of significant bit disappear after multiplication. First and second normaliser shift the dates up to 7 and 15 bits respectively. To calculate the division the operands A and X are substituted to each other and operand Y is equal to zero.
In the table the performance of designed AU is represented and is compared to the double precision floating point AUs which are implemented in similar FPGA devices.
| AU parameter | Proposed AU | AU in [1] | AU in [2]* |
| Hardware volume, CLB slices, multiply units |
1005 20 |
4625 9 |
2825 9 |
| Pipeline stages | 9 | 34 | 13 |
| Maximum clock frequency | 138 | 120 | 140 |
* division is not implemented
The project comparing shows that the proposed AU has high throughput and minimized configurable hardware volume which is in 2.8 – 4.6 times less than in AUs for similar purpose.
To implement the algorithm, usually less than n iterations are needed, each of them consists of l*n cycles of matrix multiplication, 5*n cycles of the vector multiplication and addition, and 2 divisions not to take into account the pipeline loading and flushing. The solving of the equation system with the matrix A of dimensions n=1024 and the strip width l=5 lasts about 77 milliseconds. The approximate throughput of this processor is equal to 270 Mflops.
5. Future work
When configuring the processor in new Virtex4 FPGA devices its speed will be increased approximately in two times, and the hardware volume will be decreased dramatically becauce such device supports the 35 bit multiplication and product accumulation on the structure level.
The throughput can be increased in the parallel system consisting of q such processors. Each processor node calculates the 1/q – th part of the algorithm using the loop tiling technique. Each of them can store the whole matrix A to minimize the interprocessor communications. One of the node has to gather the intermediate results, and to send the variables eps1, alpha and beta to each processor. This is the only interprocessor communications, and it could not spend much time. Therefore the speedup of the processor system is equal to q.
One modern FPGA chip can contain up to q = processor nodes. And such a system can provide up to Mflops.
6. Conclusions
The proposed rational fraction number system has the advantages that it provides higher precision than integers do, and is simpler in its implementation than the floating number system. For these advantages it can be effectively used in DSP applications which evolve the linear algebra problems.
The most advantages the rational fractions get in the modern FPGA implementation because of small hardware volume, high throughput, possibility to regulate the precision by selecting the data width. The VHDL modelling showed the possibility of use such data representation in solving linear equations by the conjugate gradient method, and showed the dependency between the data width and the maximum problem dimensions.
The experimental project of the linear equation solver showed its high throughput and small hardware volume comparing to the processor based on the floating point AU. The system of q such processor in a single FPGA device can increase the throughput in q times, where q = for modern FPGA devices.
Besides, the rational fraction calculations can get profit when the algorithms are implemented in fixed point DSP microprocessors, because they are much simpler than floating point calculations and provide the needed precision for many DSP applications.
References
1. Underwood, K.D., Hemmert, K.S.: Closing the Gap: CPU and FPGA Trends in sustained Floating Point BLAS Performance. Proc. IEEE Symp. Field Programmable Custom Computing Machines, FCCM-2004, (2004).
2. Dou, Y., Vassiliadis, S., Kuzmanov, G.K, Gaydadjiev, G.N.:64-bit Floating point FPGA Matrix Multiplication. ACM/SIGDA 13-th Int. Symp. on Field Programmable Gate Arrays, Feb., 2005, FPGA-2005, (2005), 86-95.
3. Sergyienko, A., Maslennikow, O.: Implementation of Givens QR Decomposition in FPGA. R.Wyrzykowski et al. (Eds.): PPAM 2001, Springer, LNCS, Vol.2328, (2002), 453-459.
4. Golub, G.G., Van Loan, C.F.: Matrix Computations. J.Hopkins Univ. Press. 2-d Ed. (1989), 642p.
5. Maslennikow,O., Shevtshenko,Ju., Sergyienko, A.: Configurable Microprocessor Array for DSP applications. R.Wyrzykowski et al. (Eds.): PPAM 2003, Springer, LNCS, Vol. 3019, (2004), 36-41.
6. Hintchin А.Y. Chained Fractions.: Мoshow, Nauka, 3-d Ed., (1978), 112p, (in Russian).
7. Holmes W.N. Composite Arithmetic: Proposal for a new Standard. Computer: March, №3, (1997), 65-72.
8. Irvin M.J., Smith D.R. A rational arithmetic processor.: Proc. 5-th Symp. Comput. Arithmetic, (1981), 241-244.